文章目录
- sklearn中的其他贝叶斯算法
- 一、MultinomialNB多项式贝叶斯
- sklearn中的MultinomialNB
- 二、BernoulliNB伯努利朴素贝叶斯
- 三、ComplementNB补集朴素贝叶斯
- 案例:贝叶斯做文本分类
sklearn中的其他贝叶斯算法
一、MultinomialNB多项式贝叶斯
基于原始的贝叶斯理论,但假设概率分布是服从一个简单多项式分布。可以具体解释为:实验包括n次重复试验,每项试验都有不同的可能结果。在任何给定的试验中,特定结果发生的概率是不变的。特点如下:
- 多项式擅长的是分类型变量。处理连续型变量应当使用高斯朴素贝叶斯
- 多项式实验中涉及的特性通常是离散的正整数,因此sklearn中的多项式朴素贝叶斯不接受负值输入
- 通常被用于文本分类,可以使用TF-IDF向量技术,也可以使用单词计数向量手段与贝叶斯配合

其中有:
- θ c i = 特征 X i 在 Y = c 这个分类下所有样本的取值总和 所欲特征在 Y = c 这个分类下所有样本的取值总和 \theta_{ci}=\frac{特征X_i在Y=c这个分类下所有样本的取值总和}{所欲特征在Y=c这个分类下所有样本的取值总和} θci=所欲特征在Y=c这个分类下所有样本的取值总和特征Xi在Y=c这个分类下所有样本的取值总和
- 记作 P ( X i ∣ Y = c ) P(X_{i}|Y=c) P(Xi∣Y=c),表示当Y=c这个条件固定的时候,一组样本在 这个特征上的取值被取到的概率。注意,在高斯朴素贝叶斯中求解的概率 是对于一个样本来说,而现在求解的是对于一个特征来说的概率
- α \alpha α为平滑系数,令其>0来防止训练数据中出现过的一些词汇没有出现在测试集中导致的0概率,以避免让参数为0的情况。设置为1叫做拉普拉斯平滑,如果小于1,则叫做利德斯通平滑
sklearn中的MultinomialNB

| 参数 | 含义 |
|---|---|
| alpha | 浮点数, 可不填 (默认为1.0) 拉普拉斯或利德斯通平滑的参数 ,如果设置为0则表示完全没有平滑选项。平滑相当于人为给概率加上噪音,因此 设置得越大,多项式朴素贝叶斯的精确性会越低(影响不是非常大),布里尔分数也会升高 |
| fit_prior | 布尔值, 可不填 (默认为True) 是否学习先验概率,如果设置为false,则不使用先验概率,而使用统一先验概率(uniformprior),即认为每个标签类出现的概率是 1 n _ c l a s s e s \frac{1}{n_{\_}classes} n_classes1 |
| class_prior | 形似数组的结构,结构为(n_classes, ),可不填(默认为None)类的先验概率 。如果没有给出具体的先验概率则自动根据数据来进行计算 |
一个多项式朴素贝叶斯的例子
第一步:导入模块和数据建立并归一化
from sklearn.preprocessing import MinMaxScaler
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_blobs
from sklearn.metrics import brier_score_loss
import numpy as np
class_1 = 500
class_2 = 500
centers = [[0.0,0.0],[2.0,2.0]]
clusters_std = [0.5,0.5]
X, y =make_blobs(n_samples=[class_1,class_2],
centers=centers,
cluster_std=clusters_std,
random_state=0,shuffle=False)
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
mms = MinMaxScaler().fit(Xtrain)
Xtrain_ = mms.transform(Xtrain)
Xtest_ = mms.transform(Xtest)
第二步:建立分类器并查看效果
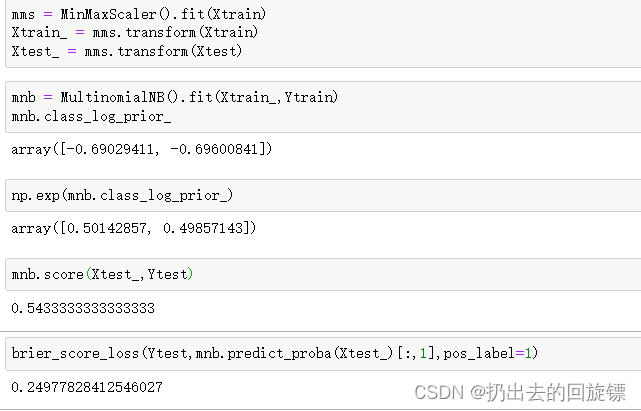
mnb = MultinomialNB().fit(Xtrain_,Ytrain)
mnb.class_log_prior_
#查看正正的概率值
np.exp(mnb.class_log_prior_)
mnb.score(Xtest_,Ytest)
brier_score_loss(Ytest,mnb.predict_proba(Xtest_)[:,1],pos_label=1)
第三步:Xtrain做哑变量再分类
from sklearn.preprocessing import KBinsDiscretizer
kbs = KBinsDiscretizer(n_bins=10, encode='onehot').fit(Xtrain)
Xtrain_ = kbs.transform(Xtrain)
Xtest_ = kbs.transform(Xtest)
mnb = MultinomialNB().fit(Xtrain_,Ytrain)
mnb.score(Xtest_,Ytest)
brier_score_loss(Ytest,mnb.predict_proba(Xtest_)[:,1],pos_label=1)
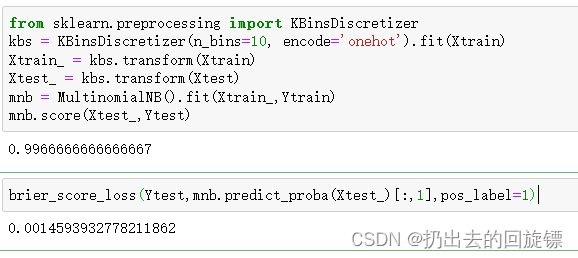
做过哑变量方式的分箱处理,多项式贝叶斯效果变好了许多
二、BernoulliNB伯努利朴素贝叶斯
伯努利朴素贝叶斯是专门处理二项分布的朴素贝叶斯。它假设数据服从多元伯努利分布,即每个特征都是二分类的,如果数据本身不是二分类,那可以使用类中专门用于二值化的参数binarize来改变数据。在处理文本分类数据时,伯努利贝叶斯通常在意“存在与否”而不是“出现次数”。通常文本较短时使用伯努利贝叶斯效果更好。
sklearn中的伯努利朴素贝叶斯
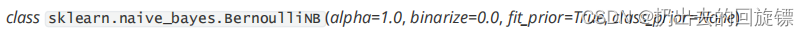
| 参数 | 含义 |
|---|---|
| alpha | 浮点数, 可不填 (默认为1.0) 拉普拉斯或利德斯通平滑的参数 ,如果设置为0则表示完全没有平滑选项。平滑相当于人为给概率加上噪音,因此 设置得越大,多项式朴素贝叶斯的精确性会越低(影响不是非常大),布里尔分数也会升高 |
| binarize | 浮点数或None,可不填,默认为0 将特征二值化的阈值,如果设定为None,则会假定说特征已经被二值化完毕 |
| fit_prior | 布尔值, 可不填 (默认为True) 是否学习先验概率,如果设置为false,则不使用先验概率,而使用统一先验概率(uniformprior),即认为每个标签类出现的概率是 1 n _ c l a s s e s \frac{1}{n_{\_}classes} n_classes1 |
| class_prior | 形似数组的结构,结构为(n_classes, ),可不填(默认为None)类的先验概率 。如果没有给出具体的先验概率则自动根据数据来进行计算 |
sklearn中简单的使用
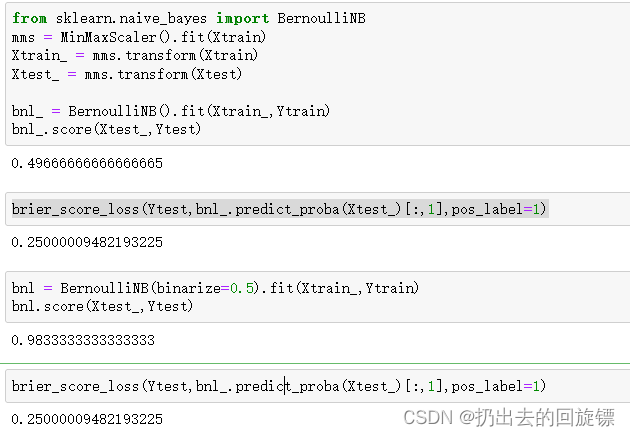
from sklearn.naive_bayes import BernoulliNB
mms = MinMaxScaler().fit(Xtrain)
Xtrain_ = mms.transform(Xtrain)
Xtest_ = mms.transform(Xtest)
#不设置二值化
bnl_ = BernoulliNB().fit(Xtrain_,Ytrain)
bnl_.score(Xtest_,Ytest)
brier_score_loss(Ytest,bnl_.predict_proba(Xtest_)[:,1],pos_label=1)
#设置二值化阈值
bnl = BernoulliNB(binarize=0.5).fit(Xtrain_,Ytrain)
bnl.score(Xtest_,Ytest)
brier_score_loss(Ytest,bnl_.predict_proba(Xtest_)[:,1],pos_label=1)
贝叶斯中样本不均衡问题
第一步:导入模块与数据
from sklearn.naive_bayes import MultinomialNB,GaussianNB,BernoulliNB
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_blobs
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.metrics import brier_score_loss as BS ,recall_score,roc_auc_score as AUC
class_1 = 50000
class_2 = 500
centers = [[0.0,0.0],[5.0,5.0]]
clusters_std = [3,1]
X,y = make_blobs(n_samples=[class_1,class_2],
centers=centers,
cluster_std=clusters_std,
random_state=0,shuffle=False)
X.shape
第二步:查看不同贝叶斯在不平衡数据集的表现
name = ["MultinomialNB","Gaussian","BernoulliNB"]
models = [MultinomialNB(),GaussianNB(),BernoulliNB()]
for name,clf in zip(name,models):
Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,y,
test_size=0.3,
random_state=420)
if name != "Gaussian":
kbs = KBinsDiscretizer(n_bins=10,encode='onehot').fit(Xtrain)
Xtrain = kbs.transform(Xtrain)
Xtest = kbs.transform(Xtest)
clf.fit(Xtrain,Ytrain)
y_pred = clf.predict(Xtest)
proba = clf.predict_proba(Xtest)[:,1]
score = clf.score(Xtest,Ytest)
print(name)
print("\tBrier:{:.3f}".format(BS(Ytest,proba,pos_label=1)))
print("\tAccuracy:{:.3f}".format(score))
print("\tRecall:{:.3f}".format(recall_score(Ytest,y_pred)))
print("\tAUC:{:.3f}".format(AUC(Ytest,proba)))
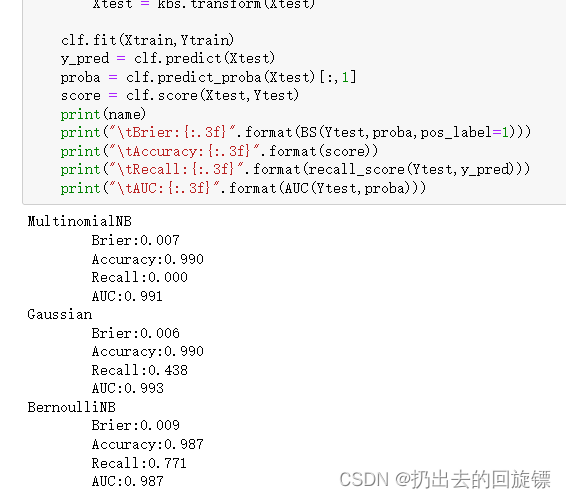
从结果看,多项式朴素贝叶斯受影响最严重,伯努利最能忍受样本不均衡问题。如果现实中,目标是捕捉少数类,可以利用补集朴素贝叶斯,它修正了包括无法处理样本不平衡在内的传统朴素贝叶斯的众多特点
三、ComplementNB补集朴素贝叶斯
CNB使用每个标签类别的补集的概念计算每个特征的权重
θ
^
i
,
y
≠
c
=
α
i
+
∑
y
j
≠
c
x
i
j
α
i
n
+
∑
i
,
y
≠
c
∑
i
=
1
n
x
i
j
\hat{\theta}_{i,y\neq c}=\frac{\alpha_i+\sum_{y_j {\neq {c} }}{x_{ij}}}{\alpha_in+\sum_{i,y\neq c}\sum_{i=1}^{n}x_{ij}}
θ^i,y=c=αin+∑i,y=c∑i=1nxijαi+∑yj=cxij
- j j j表示每个样本。 x i j x_{ij} xij表示在样本上对于特征i下的取值,在文本分类中通常是计数的值或者是TF-IDF值。 α \alpha α是像标准多项式朴素贝叶斯中一样的平滑系数。
-
∑
i
,
y
≠
c
∑
i
=
1
n
x
i
j
\sum_{i,y\neq c}\sum_{i=1}^{n}x_{ij}
∑i,y=c∑i=1nxij表示所有特征下,所有标签类别不等于c值的样本的特征取值之和。其实就是多项式分布的逆向思路

对于这个概率,对它取对数后得到权重。还可以除以它的L2范式,以解决多项式分布中特征取值比较多的样本(如比较长的文档)支配参数估计的情况。很多时候特征矩阵是稀疏矩阵,但也不排除在有一些随机事件中,可以一次在两个特征中取值的情况。
补充朴素贝叶斯一个样本的预测规则为:
p
(
Y
≠
c
∣
X
)
=
a
r
g
min
c
∑
i
x
i
w
c
i
p(Y\neq c|X)=arg\min_{c}\sum_{i}x_iw_{ci}
p(Y=c∣X)=argcmini∑xiwci
即求解出最小补集最小的标签,也就是Y=c此时最大
sklean中的补集朴素贝叶斯
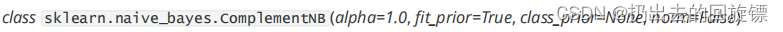
| 参数 | 含义 |
|---|---|
| alpha | 浮点数, 可不填 (默认为1.0) 拉普拉斯或利德斯通平滑的参数 ,如果设置为0则表示完全没有平滑选项。平滑相当于人为给概率加上噪音,因此 设置得越大,多项式朴素贝叶斯的精确性会越低(影响不是非常大),布里尔分数也会升高 |
| norm | 布尔值,可不填,默认False 在计算权重的时候是否适用L2范式来规范权重的大小。默认不进行规范,即不跟从补集朴素贝叶斯算法的全部内容,如果希望进行规范,请设置为True |
| fit_prior | 布尔值, 可不填 (默认为True) 是否学习先验概率,如果设置为false,则不使用先验概率,而使用统一先验概率(uniformprior),即认为每个标签类出现的概率是 1 n _ c l a s s e s \frac{1}{n_{\_}classes} n_classes1 |
| class_prior | 形似数组的结构,结构为(n_classes, ),可不填(默认为None)类的先验概率 。如果没有给出具体的先验概率则自动根据数据来进行计算 |
补集朴素贝叶斯的在不平衡样本上的表现
from sklearn.naive_bayes import ComplementNB
from time import time
import datetime
import pytz
name = ["MultinomialNB","Gaussian","BernoulliNB","Complement"]
models = [MultinomialNB(),GaussianNB(),BernoulliNB(),ComplementNB()]
for name,clf in zip(name,models):
times=time()
Xtrain, Xtest,Ytrain,Ytest = train_test_split(X,y,
test_size=0.3,
random_state=420)
if name != "Gaussian":
kbs = KBinsDiscretizer(n_bins=10,encode='onehot').fit(Xtrain)
Xtrain = kbs.transform(Xtrain)
Xtest = kbs.transform(Xtest)
clf.fit(Xtrain,Ytrain)
y_pred = clf.predict(Xtest)
proba = clf.predict_proba(Xtest)[:,1]
score = clf.score(Xtest,Ytest)
print(name)
print("\tBrier:{:.3f}".format(BS(Ytest,proba,pos_label=1)))
print("\tAccuracy:{:.3f}".format(score))
print("\tRecall:{:.3f}".format(recall_score(Ytest,y_pred)))
print("\tAUC:{:.3f}".format(AUC(Ytest,proba)))
print(datetime.datetime.fromtimestamp(time()-times,pytz.timezone('UTC')).strftime("%M:%S:%f"))

可以看到补集朴素贝叶斯牺牲了部分整体的精确度和布里尔指数,但是得到了十分高的召回率Recall,捕捉出了很多的少数类,并在此基础上维持了和原本多项式朴素贝叶斯一致的AUC分数。和其他贝叶斯算法相比,运行速度也很快。
案例:贝叶斯做文本分类
单词计数向量
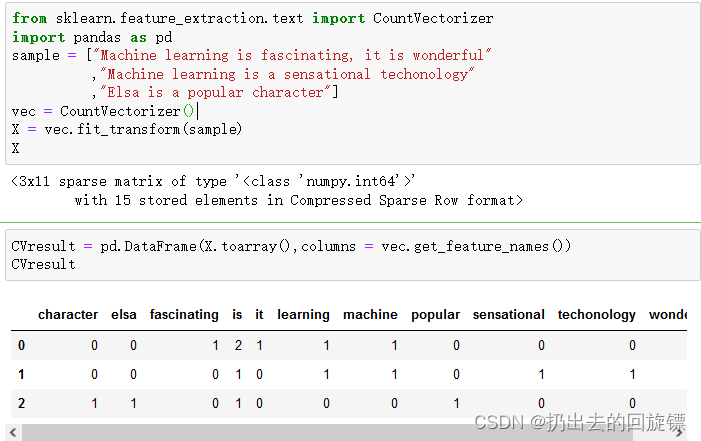
一个样本可以包含一段话或者一篇文章,一个特征代表一个单词,是一个离散的、代表次数的正整数。展示一个案例:
from sklearn.feature_extraction.text import CountVectorizer
import pandas as pd
sample = ["Machine learning is fascinating, it is wonderful"
,"Machine learning is a sensational techonology"
,"Elsa is a popular character"]
vec = CountVectorizer()
X = vec.fit_transform(sample)
X
CVresult = pd.DataFrame(X.toarray(),columns = vec.get_feature_names())
CVresult
- 对于朴素贝叶斯公式来说,如果某个句子特别长的样本会导致它贡献过大。补集贝叶斯中每个特征的权重除以自己的L2范式就是为了避免这种情况发生
- 对于许多常见的单词,即使它对语义没有过多的影响,但频率的增加会导致算法的误导。所以使用TF-IDF来处理这种现象
TF-IDF
全程term frequency-inverse document frequency,词频逆文档频率,通过单词在文档中出现的频率来衡量其权重,即IDF的大小与一个词的常见程度成反比。sklearn当中,我们使用feature_extraction.text中类TfidfVectorizer来执行这种编码
文本分类案例
第一步:导入数据以及探索数据
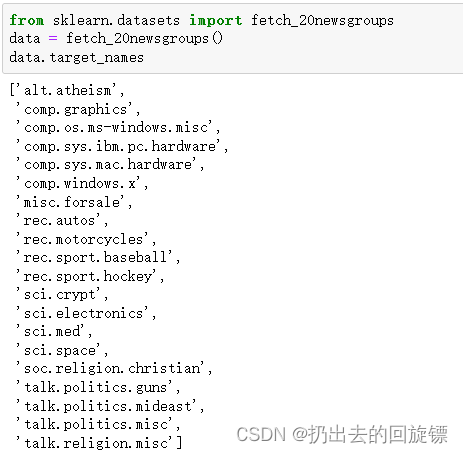
from sklearn.datasets import fetch_20newsgroups
data = fetch_20newsgroups()
data.target_names
下面是fetch_20newsgroups参数列表

| 参数 | 含义 |
|---|---|
| subset | 选择类中包含的数据子集 输入"train"表示选择训练集,“test"表示输入测试集,”all"表示加载所有的数据 |
| categories | 可输入None或者数据所在的目录 选择一个子集下,不同类型或不同内容的数据所在的目录。如果不输入默认None,则会加载全部的目录 |
| download_if_missing | 可选,默认是True 如果发现本地数据不全,是否自动进行下载 |
| shuffle | 布尔值,可不填,表示是否打乱样本顺序 对于假设样本之间互相独立并且服从相同分布的算法或模型(比如随机梯度下降)来说可能很重要 |
第二步:提取希望得到的数据集
import numpy as np
import pandas as pd
categories = ["sci.space",
"rec.sport.hockey"
,"talk.politics.guns"
,"talk.politics.mideast"] #政治 - 中东问题
train = fetch_20newsgroups(subset="train",categories = categories)
test = fetch_20newsgroups(subset="test",categories=categories)
train
#查看提取的文章类别
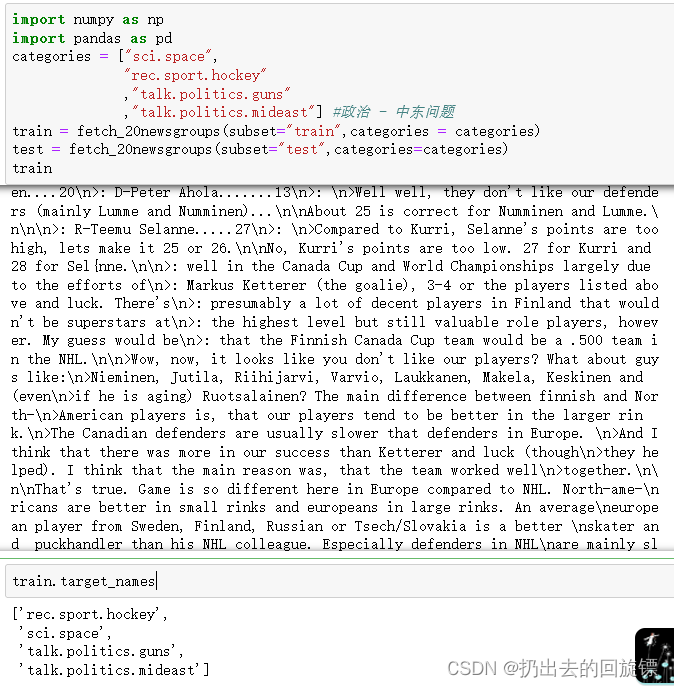
train.target_names
#查看文章总数
len(train.data)
#提取某一篇文章
train.data[11]
#查看标签
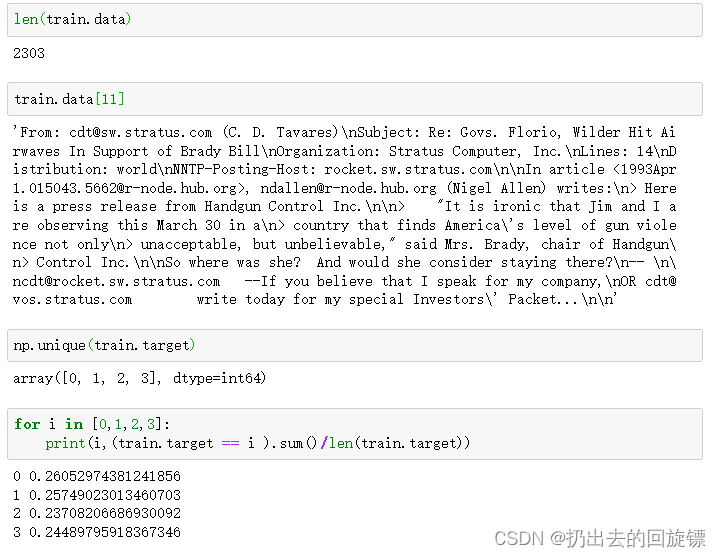
np.unique(train.target)
#查看是否有样本不平衡问题
for i in [0,1,2,3]:
print(i,(train.target == i ).sum()/len(train.target))
第三步:使用TF-IDF将文本编码
from sklearn.feature_extraction.text import TfidfVectorizer as TFIDF
Xtrain = train.data
Xtest = test.data
Ytrain = train.target
Ytest = test.target
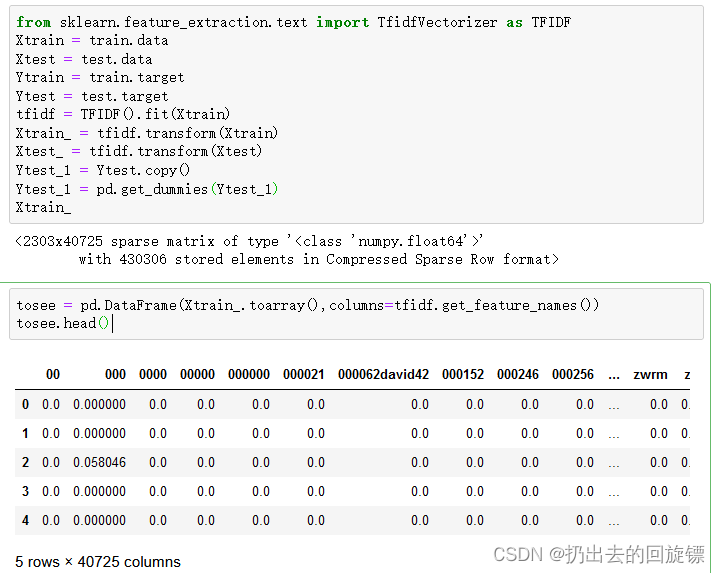
tfidf = TFIDF().fit(Xtrain)
Xtrain_ = tfidf.transform(Xtrain)
Xtest_ = tfidf.transform(Xtest)
Ytest_1 = Ytest.copy()
Ytest_1 = pd.get_dummies(Ytest_1)
Xtrain_
tosee = pd.DataFrame(Xtrain_.toarray(),columns=tfidf.get_feature_names())
tosee.head()
第四步:在贝叶斯上分别建模,查看结果
from sklearn.naive_bayes import MultinomialNB,ComplementNB,BernoulliNB
from sklearn.metrics import brier_score_loss as BS
name = ["Multinomial","Complement","Bournulli"]
models = [MultinomialNB(),ComplementNB(),BernoulliNB()]
for name,clf in zip(name,models):
clf.fit(Xtrain_,Ytrain)
y_pred = clf.predict(Xtest_)
proba = clf.predict_proba(Xtest_)
score = clf.score(Xtest_,Ytest)
print(name)
Bscore = []
for i in range(len(np.unique(Ytrain))):
bs = BS(Ytest_1[i],proba[:,i])
Bscore.append(bs)
print("\tBrier uder{}:{:.3f}".format(train.target_names[i],bs))
print("\tAverage Brier:{:.3f}".format(np.mean(Bscore)))
print("\tAccuracy:{:.3f}".format(score))
print("\n")

可以看到补集贝叶斯分数更高,但精确度更高。使用概率校准来进行突破:
from sklearn.calibration import CalibratedClassifierCV
name = ["Multinomial"
,"Multinomial + Isotonic"
,"Multinomial + Sigmoid"
,"Complement"
,"Complement + Isotonic"
,"Complement + Sigmoid"
,"Bernoulli"
,"Bernoulli + Isotonic"
,"Bernoulli + Sigmoid"]
models = [MultinomialNB()
,CalibratedClassifierCV(MultinomialNB(), cv=2, method='isotonic')
,CalibratedClassifierCV(MultinomialNB(), cv=2, method='sigmoid')
,ComplementNB()
,CalibratedClassifierCV(ComplementNB(), cv=2, method='isotonic')
,CalibratedClassifierCV(ComplementNB(), cv=2, method='sigmoid')
,BernoulliNB()
,CalibratedClassifierCV(BernoulliNB(), cv=2, method='isotonic')
,CalibratedClassifierCV(BernoulliNB(), cv=2, method='sigmoid')
]
for name,clf in zip(name,models):
clf.fit(Xtrain_,Ytrain)
y_pred = clf.predict(Xtest_)
proba = clf.predict_proba(Xtest_)
score = clf.score(Xtest_,Ytest)
print(name)
Bscore = []
for i in range(len(np.unique(Ytrain))):
bs = BS(Ytest_1[i],proba[:,i])
Bscore.append(bs)
print("\tBrier uder{}:{:.3f}".format(train.target_names[i],bs))
print("\tAverage Brier:{:.3f}".format(np.mean(Bscore)))
print("\tAccuracy:{:.3f}".format(score))
print("\n")
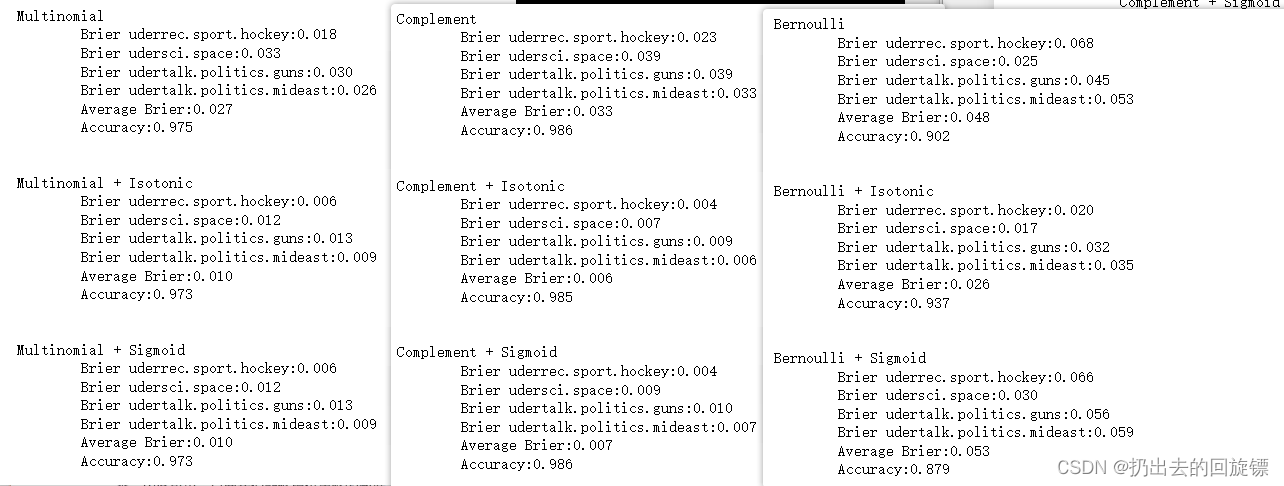
通过比较,补集贝叶斯使用Sigmoid进行概率校准时的模型综合最优秀。对于机器学习而言,朴素贝叶斯也许不是最常用的方法,但由于它的简单快捷还是占有一席之地。只要能够提供足够的证据,合理利用高维数据进行训练,朴素贝叶斯就可以提供不错的效果。