一、多源BFS
在上一篇博客:广度优先搜索BFS基础中,我们接触到的BFS均是单起点(单源)的,但是对于某一些问题,其有多个起点,此类问题我们称为多源BFS问题。先思考下面一道例题:
1.腐烂的橘子
本题我们首先需要意识到是一个搜索问题,一个新鲜的橘子变为腐烂状态需要的最少时间实际上就相当于我们从离它最近的腐烂的橘子开始走到它所在位置需要的最少步数(当然也可能走不到),现在的问题实际就是一个BFS经典问题,但关键在于一开始腐烂的橘子有多个,也就是说BFS的起点有多个,这是一个多源BFS。
如何求解多源BFS?实际上与单源BFS完全相同!我们假定存在一个虚拟结点,其到所有多源BFS起点的距离均相同,且为0。那么从这些起点出发到达某一个结点的最短路就等于从这个虚拟结点出发到达该结点的最短路,而此时问题则转化了一个我们再熟悉不过的单源BFS问题,在实际代码编写中只需要在一开始将所有的起点都入队即可,其余部分与单源BFS完全相同。
在本题中还有几个要点:首先,求的是所有新鲜的橘子变腐败的最短时间,BFS求得的是到起点到每个结点的最短距离,而所有结点都到达的最短时间就是到这些结点的最短距离中最大的那个;其次,可能出现有橘子不可能变腐败的情形,此时只用在一开始保存有多少新鲜的橘子,后续在BFS过程中,能到达的橘子都将腐败,新鲜橘子个数减去所有能到达的橘子数,如果结果不为0则说明存在有不可能变腐败的橘子。示例代码如下:
class Solution {
public int orangesRotting(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
Deque<Point> q = new ArrayDeque<>();
int cnt = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 1) {
cnt++;
}
// 将所有的起点全部入队
if (grid[i][j] == 2) {
q.add(new Point(i, j, 0));
grid[i][j] = 0;
}
}
}
int ans = 0;
while (!q.isEmpty()) {
Point tmp = q.poll();
for (int i = 0; i < 4; ++i) {
int x = tmp.x + dx[i];
int y = tmp.y + dy[i];
if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] != 0) {
int step = tmp.step + 1;
cnt--;
ans = Math.max(ans, step);
q.add(new Point(x, y, step));
grid[x][y] = 0;
}
}
}
return cnt == 0 ? ans : -1;
}
int[] dx = {-1, 1, 0 , 0};
int[] dy = {0, 0 , -1, 1};
class Point {
int x;
int y;
int step;
public Point(int x, int y, int step) {
this.x = x;
this.y = y;
this.step = step;
}
}
}二、优先队列BFS
在使用普通队列的BFS中,我们只能求无权图的最短路(或者是各个边权均相等的带权图),如果面对的是一张带权图(各个边权可能不等),我们如何用BFS来求其最短路?先从如下一道例题开始:
1.拯救行动
该题在传统的迷宫问题上做出了一点改动,即走到有守卫的位置其权值不再是1,而是2,这样该图就是一张边权为1或者2的带权图。无权图之所以能用BFS求解,是由于它的边权默认均等于1,离起点的距离就等于层数。而在带权图中,一个结点离起点的层数小,并不能代表它们间的距离就小,因为这取决于它们路径间的边权,所以普通BFS并不能求得带权图的最短路。
实际上,求带权图的最短路有一系列专门的算法,其被称为最短路径算法,均采用了动态规划的思想,我们先来介绍其中的一种:

对于上面一张带权图,要求得A~F的最短路,假设我们已知与终点F相连的结点D和结点E到起点A的最短路,记为f(A,D)和f(A,E),那么f(A,F)=min{ f(A,D)+4, f(A,E)+2 },同理对其它结点也如此分析从结点BC开始计算就能求得所有结点的最短路,这就是用动态规划求解一般的带权图最短路径的思路。那么,我们是否可以用BFS模拟出这个过程?答案是可以的,而这其实就是著名的dijkstra算法,是求解一般带权图最短路问题最常用的方法之一。所以如果要解决这种矩阵每个位置的权值不相等的迷宫问题,我们可以将其转化为带权图,利用dijkstra算法求解,如下面一个迷宫矩阵就可以转化为右边的带权图:
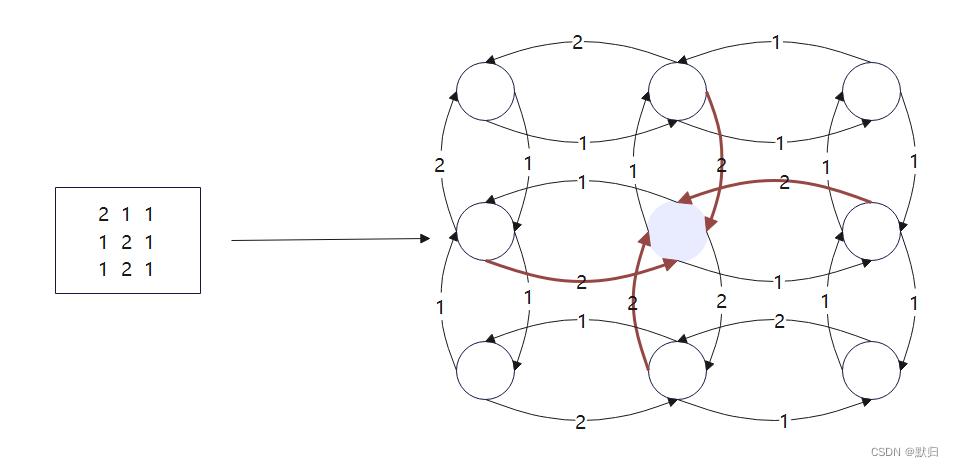
但是,有没有细心的读者发现,右边转化来的带权图上具备着一个相当显著的特征——到达每个结点的所有边其权值一定相等!发现这一特征后,我们可以对dijkstra算法进行简化:如果在一副带权图中,与终点相连的边权始终相等,我们设为n,带入终点最短路计算公式里:f(A,F)=min{ f(A,D)+n, f(A,E)+n }=min{f(A,D), f(A,E)}+n,这时我们发现,要求到终点的最短路,只用找到和它相连的结点的最短路中的最小值即可,而要实现这个过程实际上我们只要将普通BFS中的队列替换成优先队列即可,如果我们从优先队列取出一个结点,而它能扩展出终点,那该路径就是最短路。
why?我们知道BFS能将图划分出层次,当我们从优先队列取出一个结点时,它一定是同层次下结点中离起点最短的,因为此时同层次下的结点只有两种状态:
一、被扩展出了,那没什么好说的因为优先队列取出的就是最小的;
二、没被扩展出,那说明还没到该层次其最短路就已经大于该结点了,要到达该层次还需要经过几条边,距离只会比它大(图中没有负边权)。
综上,该结点一定是同层次下结点中离起点最短的。
本题的示例代码如下(可以看到与BFS的模板区别仅仅在于普通队列换成了优先队列):
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
for (int k = 0; k < t; ++k) {
int m = sc.nextInt();
int n = sc.nextInt();
char[][] map = new char[m][n];
// 优先队列
PriorityQueue<Point> q = new PriorityQueue<>(Comparator.comparingInt(a -> a.step));
sc.nextLine();
for (int i = 0; i < m; ++i) {
String s = sc.nextLine();
for (int j = 0; j < n; ++j) {
map[i][j] = s.charAt(j);
if (map[i][j] == 'r') {
q.add(new Point(i, j, 0));
}
}
}
boolean flag = false;
loop:
while (!q.isEmpty()) {
Point tmp = q.poll();
for (int i = 0; i < 4; ++i) {
int x = tmp.x + dx[i];
int y = tmp.y + dy[i];
if (x >= 0 && x < m && y >= 0 && y < n && map[x][y] != '#') {
if (map[x][y] == 'a') {
System.out.println(tmp.step + 1);
flag = true;
break loop;
}
int tag = map[x][y] != 'x' ? 1 : 2;
q.add(new Point(x, y, tmp.step + tag));
map[x][y] = '#';
}
}
}
if (!flag) {
System.out.println("Impossible");
}
}
}
static int[] dx = {-1, 1, 0 , 0};
static int[] dy = {0 , 0, -1, 1};
static class Point {
int x;
int y;
int step;
public Point(int x, int y, int step) {
this.step = step;
this.x = x;
this.y = y;
}
}
}2.最小传输时延(华为od机试题)
有M*N的节点矩阵,每个节点可以向8个方向(上、下、左、右及四个斜线方向)转发数据包,每个节点转发时会消耗固定时延(等于该节点上的权值),连续两个相同时延可以减少一个时延值,即当有K个相同时延的节点连续转发时可以减少K- 1个时延值。求从左上角(0,0)开始转发数据包到右下角(M-1,N- 1)的最短时延。
输入示例:
3 3
0 2 2
1 2 1
2 2 1输出示例:
3
本题虽然背景不是迷宫问题,但是本质上并无区别,同样适用于优先队列BFS的使用条件。但该问题中多了一个连续k个相同权值将减少k-1的距离的条件,因此存入优先队列的节点类需要多维护一个自身的权值。示例代码如下:
import java.util.PriorityQueue;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int m = sc.nextInt(), n = sc.nextInt();
int[][] dis = new int[m][n];
for(int i=0; i<m; ++i) {
for(int j=0; j<n; ++j) {
dis[i][j] = sc.nextInt();
}
}
int dx[] = {-1, 1 ,0 , 0 , -1 , 1 , -1, 1};
int dy[] = {0 , 0 ,-1, 1 , -1 , -1, 1 , 1};
boolean[][] vit = new boolean[m][n];
for(int i=0; i<m; ++i) {
for(int j=0; j<n; ++j) {
vit[i][j]=false;
}
}
PriorityQueue<Node> q = new PriorityQueue<>((a,b)->(a.dis-b.dis));
q.add(new Node(dis[0][0],0,0,dis[0][0]));
vit[0][0]=true;
while(!q.isEmpty()) {
Node node = q.poll();
for(int i=0; i<8; ++i) {
int x = node.x+dx[i], y = node.y+dy[i];
if((x >=0 && x < m) && (y >= 0 && y <n ) && !vit[x][y]) {
// 如果时延连续相同,-1
int t = node.dis + dis[x][y] + (dis[x][y] == node.val ? -1 : 0);
if(x == m-1 && y == n-1) {
System.out.println(t);
return;
}
q.add(new Node(t, x, y, dis[x][y]));
vit[x][y] = true;
}
}
}
}
}
class Node{
int dis;
int x;
int y;
int val; // 与上题比较,多维护了自身的权值
public Node(int dis,int i,int j,int val) {
this.dis = dis;
this.x = i;
this.y = j;
this.val = val;
}
}
三、双端队列BFS
到此为止,对于无权图或者边权不为负且与终点相连的边权相等的带权图,我们都有相应的BFS方法了。不过我们再来考虑一种特殊的图——边权只为0或1的带权图,对于这样的图,按我们已掌握的知识应该使用优先队列BFS,但实际上,当边权为0时它将不会影响当前的最短路状况,只有当边权为1时最短路才会受到影响,如果我们一开始就约定好顺序,遇到边权为0的边我们将其放到队列的最前面,遇到边权为1的边我们将其放到队列的最后面,这样其实就已经保证了整个队列的有序性,每次我们取出队头的元素一定是队列中的最小值,这样我们就可以利用一个双端队列来替代优先队列,将时间复杂度从O(logn)缩减到O(1)。
对于为什么0放队首、1放队尾就能保证队列有序(实际上不一定是0或1,对于0或其它任意值都满足),读者可以自己试一试, 从空队列开始,逐渐添加为0或者为1的元素,你会发现整个队列一定保证有序,且分成明显的两份,每一份的元素分别相等,且前一份的元素总比后一份小1。
1.拖拉机
该题是标准的模板题,有草垛的位置记为1,没有的位置记为0,就是一张边权只为0或1的带权图,直接使用双端BFS求解。示例代码如下:
import java.util.*;
public class Main {
static int[][] maze = new int[2000][2000];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int tx = sc.nextInt();
int ty = sc.nextInt();
int maxX = 0, maxY = 0;
for (int i = 0; i < n; ++i) {
int p = sc.nextInt();
maxX = Math.max(maxX, p);
int q = sc.nextInt();
maxY = Math.max(maxY, q);
maze[p][q] = 1;
}
ArrayDeque<Point> que = new ArrayDeque<>();
que.add(new Point(tx, ty, 0));
while (!que.isEmpty()) {
Point tmp = que.poll();
for (int i = 0; i < 4; ++i) {
int x = tmp.x + dx[i];
int y = tmp.y + dy[i];
if (x >= 0 && x <= maxX + 1 && y >= 0 && y <= maxY + 1 && maze[x][y] != -1) {
if (x == 0 && y == 0) {
System.out.println(tmp.dis + maze[x][y]);
return;
}
if (maze[x][y] == 0) {
que.addFirst(new Point(x, y, tmp.dis));
} else {
que.addLast(new Point(x, y, tmp.dis + 1));
}
maze[x][y] = -1;
}
}
}
}
static int[] dx = {0, 0, 1,-1};
static int[] dy = {1,-1, 0, 0};
static class Point {
int x;
int y;
int dis;
public Point(int x, int y, int dis) {
this.x = x;
this.y = y;
this.dis = dis;
}
}
}2.电路维修
本题不同于常见的BFS题,不能对给出的矩阵直接进行BFS搜索,因为该矩阵并不能转换成一张图,我们需要利用矩阵的信息来建图。
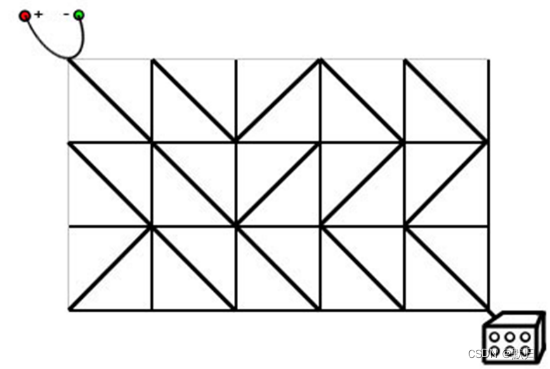
从上图来看,如果将每个行列的交叉点当作顶点,那矩阵中保存的电路方向就可以作为权值,若两个顶点位于一个方块的左上和右下,而方块中的电路方向为 \ ,则这两个顶点连通,边权为1,否则为0,若两个顶点位于一个方块的左下和右上,而方块中的电路方向为 / ,则这两个顶点连通,边权为1,否则为0。这样,本题就变成了一个边权只有0和1的带权图最短路问题,利用双端队列BFS求...解?注意!本题务必要小心一个陷阱,那就是这个带权图中,到每个顶点的边权不一定相等!既可能包含0也可能包含1,而非只包含0或只包含1!这样就不满足双端队列BFS求解的条件了,所以最终本题要使用dijkstra算法,不过里面的优先队列可以换成双端队列。示例代码如下:
import java.util.*;
public class Main {
static int m, n;
static int[][] maze;
static int[] dx = { -1, -1, 1, 1 }, dy = { -1, 1, 1, -1 };
static int[] ix = { -1, -1, 0, 0 }, iy = { -1, 0, 0, -1 };
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
m = sc.nextInt();
n = sc.nextInt();
sc.nextLine();
maze = new int[m][n];
for (int i = 0; i < m; ++i) {
String s = sc.nextLine();
for (int j = 0; j < n; ++j) {
maze[i][j] = s.charAt(j) == '/' ? -2 : 0; // 边权矩阵
}
}
boolean[][] vis = new boolean[m + 1][n + 1];
int[][] dist = new int[m + 1][n + 1];
for(int[] array : dist) {
Arrays.fill(array, 0x3f3f3f3f);
}
dist[0][0] = 0;
ArrayDeque<int[]> que = new ArrayDeque<>();
que.add(new int[] {0, 0});
while (!que.isEmpty()) {
int[] tmp = que.poll();
if (tmp[0] == m && tmp[1] == n) {
System.out.println(dist[tmp[0]][tmp[1]]);
return;
}
if(vis[tmp[0]][tmp[1]]) {
continue;
}
vis[tmp[0]][tmp[1]] = true;
for (int i = 0; i < 4; ++i) {
// dx,dy是在顶点矩阵上移动,顶点矩阵就是所有行列的交点
int x = tmp[0] + dx[i], y = tmp[1] + dy[i];
// ix,iy是在边权矩阵上移动
int p = tmp[0] + ix[i], q = tmp[1] + iy[i];
if (x < 0 || x > m || y < 0 || y > n) {
continue;
}
// 若两个顶点位于一个方块的左上和右下,而方块中的电路方向为 \ ,则这两个顶点连通,边权为1,否则为0,若两个顶点位于一个方块的左下和右上,而方块中的电路方向为 / ,则这两个顶点连通,边权为1,否则为0。
int dis = maze[p][q] == (dx[i] ^ dy[i]) ? 0 : 1;
if (dist[tmp[0]][tmp[1]] + dis <= dist[x][y]) {
dist[x][y] = dist[tmp[0]][tmp[1]] + dis;
if (dis == 0) {
que.addFirst(new int[]{x, y});
} else {
que.addLast(new int[]{x, y});
}
}
}
}
System.out.println("NO SOLUTION");
}
}四、对几种不同队列BFS的总结
- 普通队列BFS:适用于无权图
- 双端队列BFS:适用于边权仅包含0或1且到每个顶点的边权都相等的带权图
- 优先队列BFS:适用于边权不为负且到每个顶点的边权都相等的带权图
- 如果图上到每个顶点的边权不等,则需使用最短路算法