模拟

class Solution {
public:
    vector<int> resultArray(vector<int> &nums) {
        vector<int> r1{nums[0]}, r2{nums[1]};
        for (int i = 2; i < nums.size(); i++) {
            if (r1.back() > r2.back())
                r1.push_back(nums[i]);
            else
                r2.push_back(nums[i]);
        }
        for (auto x: r2)
            r1.push_back(x);
        return r1;
    }
};

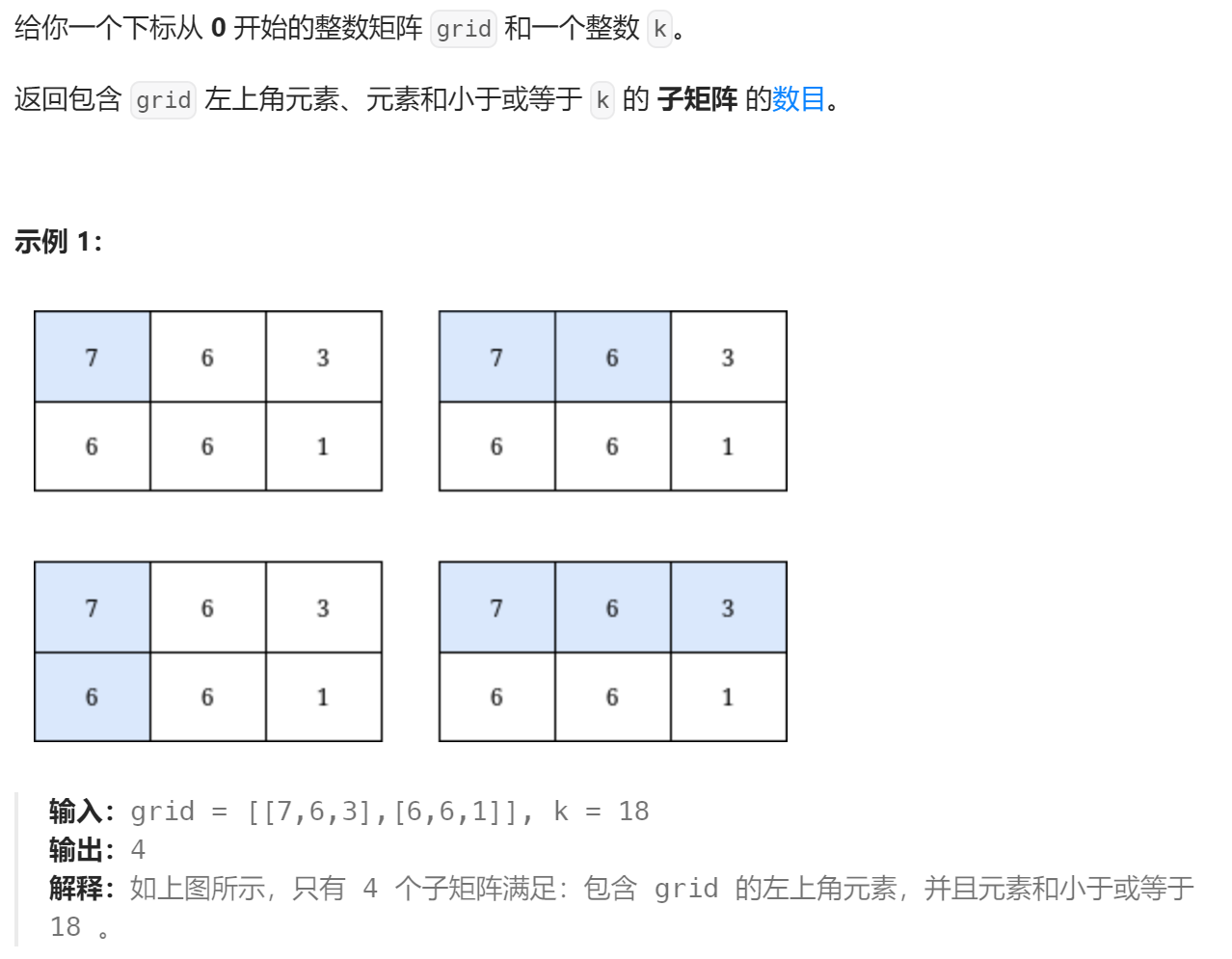
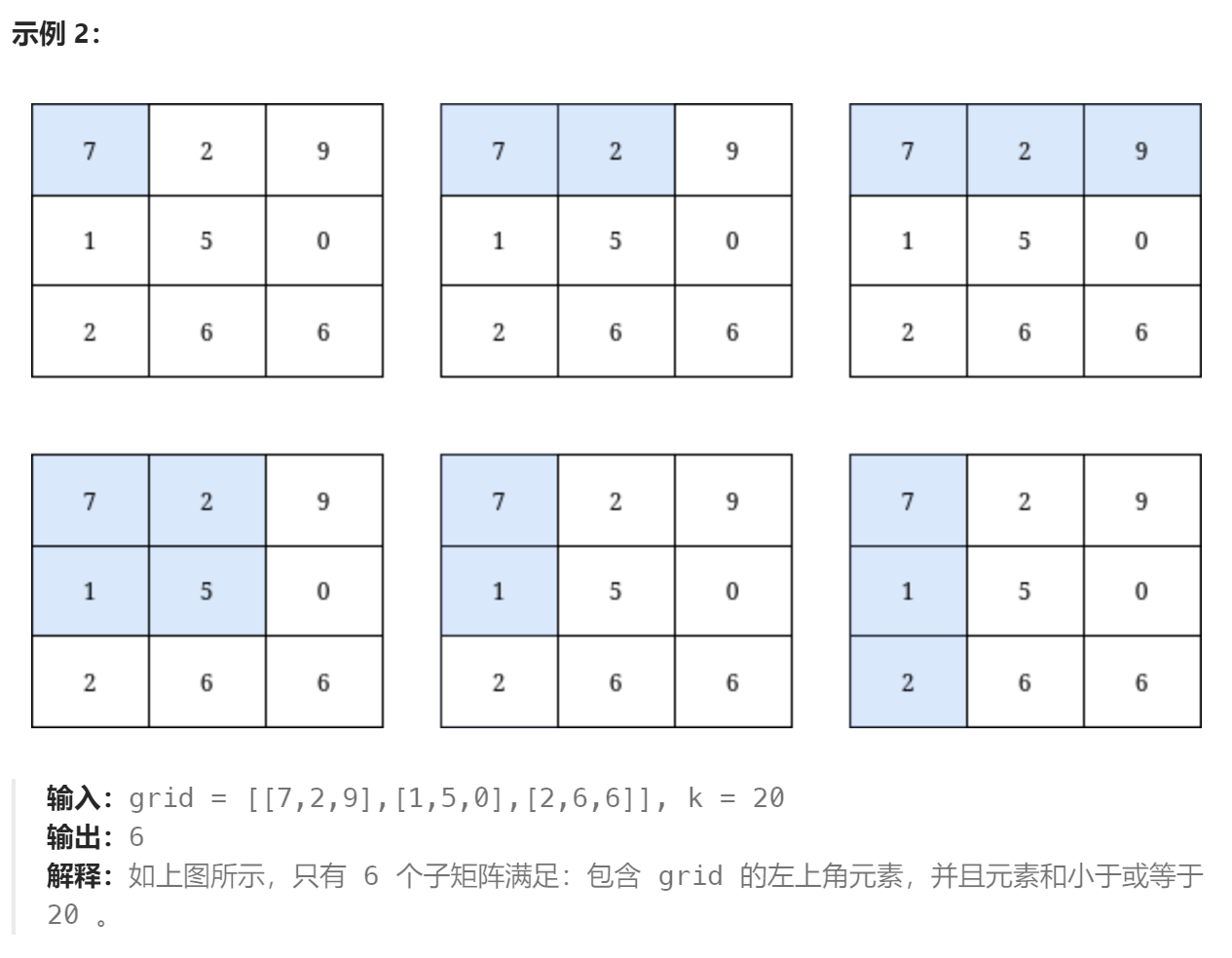
前缀和：先计算二维前缀和，再枚举包含左上角元素的子矩阵

class Solution {
public:
    int countSubmatrices(vector<vector<int>> &grid, int k) {
        int m = grid.size(), n = grid[0].size();
        for (int i = 0; i < m; i++)
            for (int j = 1; j < n; j++)
                grid[i][j] += grid[i][j - 1];
        for (int j = 0; j < n; j++)
            for (int i = 1; i < m; i++)
                grid[i][j] += grid[i - 1][j];
        int res = 0;
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
                if (grid[i][j] <= k)
                    res++;
        return res;
    }
};

枚举：枚举属于 Y 和不属于 Y 的单元格的颜色

class Solution {
public:
    int minimumOperationsToWriteY(vector<vector<int>> &grid) {
        int n = grid.size();
        int res = INT32_MAX;
        for (int cy = 0; cy <= 2; cy++)//属于Y的单元格的颜色
            for (int cny = 0; cny <= 2; cny++)//不属于Y的单元格的颜色
                if (cy != cny) {
                    int t = 0;
                    for (int i = 0; i < n; i++)
                        for (int j = 0; j < n; j++)
                            if (i <= n / 2 && (i == j || i + j == n - 1) || i > n / 2 && j == n / 2)//属于Y的单元格
                                t += grid[i][j] != cy ? 1 : 0;
                            else
                                t += grid[i][j] != cny ? 1 : 0;
                    res = min(res, t);
                }
        return res;
    }
};

离散化 + 树状数组：先将 nums 离散化，然后利用树状数组来维护两个数组，并查询数组中严格大于某个数的元素数量

class Solution {
public:
    vector<int> resultArray(vector<int> &nums) {
        vector<int> li = nums, o = li;
        sort(o.begin(), o.end());
        o.erase(unique(o.begin(), o.end()), o.end());
        for (auto &i: li)//li为nums离散化后的数组
            i = lower_bound(o.begin(), o.end(), i) - o.begin() + 1;
        int n = nums.size();
        int m = li.size();
        vector<int> r1{nums[0]}, r2{nums[1]};
        BinaryIndexedTree t1(m), t2(m);//两个树状数组
        t1.add(li[0], 1);
        t2.add(li[1], 1);
        for (int i = 2; i < n; i++) {
            int c1 = t1.query(m) - t1.query(li[i]);
            int c2 = t2.query(m) - t2.query(li[i]);
            if (c1 > c2) {
                r1.push_back(nums[i]);
                t1.add(li[i], 1);
            } else if (c1 < c2) {
                r2.push_back(nums[i]);
                t2.add(li[i], 1);
            } else {
                if (r1.size() <= r2.size()) {
                    r1.push_back(nums[i]);
                    t1.add(li[i], 1);
                } else {
                    r2.push_back(nums[i]);
                    t2.add(li[i], 1);
                }
            }
        }
        for (auto x: r2)
            r1.push_back(x);
        return r1;
    }

    class BinaryIndexedTree {//树状数组模板
    public:
        int N;
        vector<int> a;

        BinaryIndexedTree(int n) {
            N = n;
            a = vector<int>(N + 1);
        }

        inline int lowbit(int x) {
            return x & -x;
        }

        void add(int loc, int val) {// li[loc]+=val;
            for (; loc <= N; loc += lowbit(loc))
                a[loc] += val;
        }

        int query(int loc) {// sum{li[k] | 1<=k<=loc}
            int res = 0;
            for (; loc > 0; loc -= lowbit(loc))
                res += a[loc];
            return res;
        }
    };
};