目录

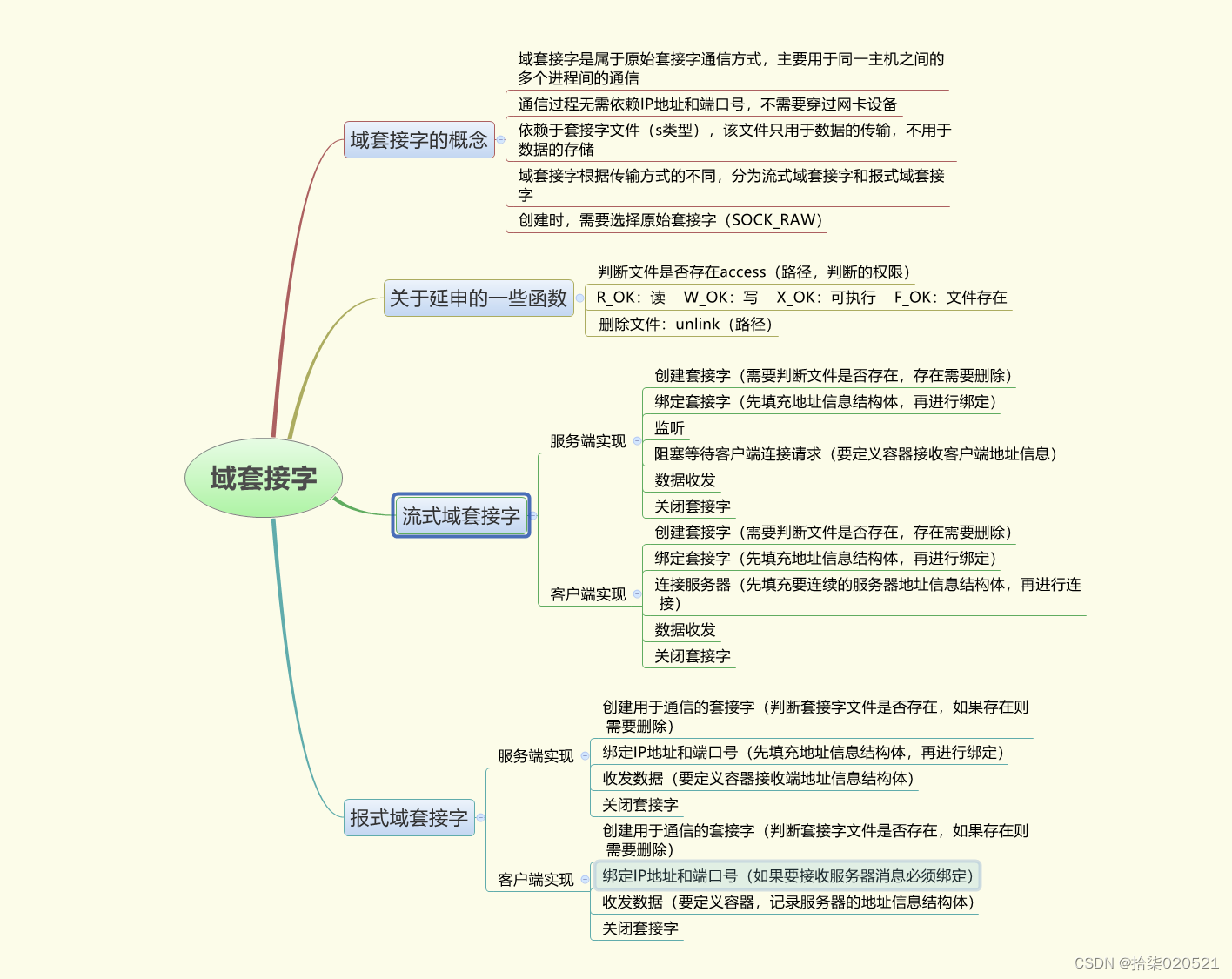
 一、自适应控制算法的基本原理

 二、自适应控制算法分类

三、案例

 3.1自适应PID控制

1） 模型识别

2）动态调整PID参数逻辑

3）PID控制器

---

  自适应控制算法是一种高级控制算法，用于处理那些参数不确定或者动态变化的系统。这类算法能够根据系统性能的实时反馈自动调整控制器参数，以保持系统性能在最优或接近最优状态。自适应控制特别适用于模型不准确、系统参数随时间变化或环境条件变化显著的情况。 

一、自适应控制算法的基本原理

    自适应控制算法的核心思想是在控制过程中不断地识别系统的动态特性，并相应地调整控制策略，以适应这些变化。这通常涉及两个主要步骤：

1）参数估计或系统识别

算法实时估计系统参数或识别系统模型。这可以通过各种方法实现，如最小二乘法、梯度下降法或其他优化技术。

2）控制器参数调整

基于估计出的系统参数或识别出的模型，算法调整控制器的参数，以改善系统性能。

 二、自适应控制算法分类

 1）模型参考自适应控制（MRAC）

 该方法设计一个期望的模型参考系统，该系统表现出期望的动态性能。控制策略的目标是调整控制器参数，使实际系统的输出跟踪模型参考输出

2）自校正控制（STR）

   该方法不需要模型参考。相反，它直接在控制律中引入自适应机制，根据系统输出和控制输入的实时数据调整控制器参数，以达到期望的控制目标。

三、案例

 3.1自适应PID控制

根据实时反馈动态调整其PID参数（比例Kp、积分Ki、微分Kd）以适应系统变化的控制器。

1） 模型识别

动态估计系统的模型参数，以便更准确地调整PID参数

假设有一个线性系统模型

• y(t) 是在时间 t 的系统输出。
• θ 是系统模型参数的向量，这是我们想要估计的。
• ϕ(t) 是包含系统输入和/或输出历史值的特征向量。
• ε(t) 是测量噪声。

采用递归最小二乘法RLS进行模型动态参数更新：

参数估计更新公式:

其中

是基于上一时刻参数估计的输出预测，K(t) 是增益向量，用于调整估计的更新量。

其中增益K(t) 的计算为：

λ 是遗忘因子，用于调整历史数据的权重，P(t−1) 是参数估计误差协方差矩阵。

其中协方差矩阵P(t−1) 的更新公式：

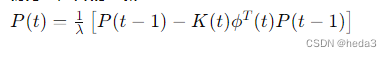
 因此通过上述的递归可实现模型的参数估计。

# 控制输入：u  系统输出：y
void RLS_Update(float u, float y) {
    static float phi = 0.0; // 系统输入（或状态）的历史值

    // 计算增益
    float K = P * phi / (lambda + phi * P * phi);

    // 更新参数估计
    theta_hat += K * (y - theta_hat * phi);

    // 更新误差协方差
    P = (1 - K * phi) * P / lambda;

    // 更新历史值
    phi = u; // 假设u是当前的输入（或状态）
}

//输出更新的模型参数theta_hat 

2）动态调整PID参数逻辑

根据模型识别的结果和系统性能反馈，设计更精细的控制参数调整逻辑：

void adaptPIDParameters(float error, float dError, float modelParams) {
    // 根据误差、误差变化率和模型参数调整PID参数
    // 根据误差的绝对值调整Kp
    if (abs(error) > 5) {
        Kp += 0.1;  // 如果误差较大，增加Kp
    } else if (abs(error) < 2) {
        Kp -= 0.1;  // 如果误差较小，减小Kp
    }

    // 确保Kp不会变得太小或太大
    if (Kp < 0.1) Kp = 0.1;
    if (Kp > 10.0) Kp = 10.0;
    // 可能需要更多条件和调整策略
}

3）PID控制器

float pidControl(float setpoint, float temperature) {
    float error = setpoint - temperature;
    integral += error;  // 积分项
    float derivative = error - prev_error;  // 微分项
    prev_error = error;

    return Kp*error + Ki*integral + Kd*derivative;
}

int main() {
    float input, output; // 控制输入和输出
   // RLS算法参数
   float lambda = 0.99; // 遗忘因子，一般选择接近1的值
   float P = 1.0; // 估计误差协方差的初始值
   float theta_hat = 0.0; // 参数估计的初始值，模型参数modelParams

    for (int cycle = 0; cycle < 100; cycle++) {
        // 模拟获取系统输出（实际该部分不存在，通过传感器测量反馈输出）
        output = simulateSystem(input);

        // 模型识别 modelIdentification
        RLS_Update(input, output);

        // 根据当前误差和模型参数调整PID参数
        float error = setpoint - output;
        float dError = error - prev_error;
        adaptPIDParameters(error, dError, theta_hat);

        // 计算控制输入
        input = pidControl(error, dError);
        
        // 模拟将控制输入应用到系统
        // 更新系统状态
    }
    return 0;
}