【数据结构】20 树的应用（堆及其操作）

news2024/7/6 17:39:25

堆的定义

堆是一种优先队列，从堆中取出元素时按照元素的优先级大小，而不是元素进入队列的先后顺序。
堆的最常用结构是二叉树，一般为完全二叉树。通常使用数组来实现堆的存储。
最大堆：任一结点的值大于或等于其子节点的值。这一性质决定了根节点元素的值在整个堆里是最大的。
最小堆：任一结点的值小于或等于其子节点的值。这一性质决定了根节点元素的值在整个堆里是最小的。
需要注意的是，兄弟节点之间没有什么约束关系，比如 可能会出现左子树个节点的值都大于右子树的所有结点

最大堆的操作

一个有N个元素的最大堆H是一颗完全二叉树，每个结点上的元素值不小于其子节点元素的值。

最大堆的创建

typedef int ElementType;
typedef struct Hnode* Heap;
struct Hnode {
	ElementType* Data;
	int size;
	int capacity;
};

//若堆里要有n个元素，则开辟的数组要有n+1大小，因为0下标位置无用，从1处开始存储
Heap CreateHeap(int maxsize) {
	Heap H = new Hnode[maxsize];
	H->capacity = maxsize ;
	H->Data = new ElementType[maxsize + 1];
	H->size = 0;
	H->Data[0] = 1e8;//定义哨兵为大于堆中所有可能元素的数值
	return H;
}

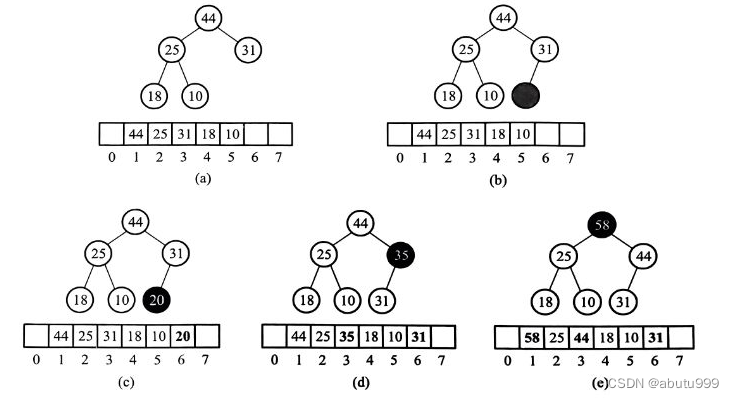
元素的插入

从新增结点的最后一个结点的父节点开始，用要插入的元素向下过滤上层结点。
在这里插入图片描述

bool IsFull(Heap H) {
	if (H->size == H->capacity) {
		return true;
	}
	else {
		return false;
	}
}
bool Insert(Heap H, ElementType X) {
	//H->Data[0]为哨兵
	if (IsFull(H)) {
		printf("最大堆已满\n");
		return false;
	}

	int i = ++H->size;
	//H->Data[i/2]为其父结点 
	while (H->Data[i / 2] < X) {
		H->Data[i] = H->Data[i / 2];
		i /= 2;

	}
	H->Data[i] = X;
	return true;


}


void printh(Heap h) {
	queue<int> q;
	int i = 1;
	int j;
	q.push(i);
	while (!q.empty()) {
		j = q.front();
		printf("%d ", h->Data[j]);
		q.pop();
		if (2 * j <= h->size) {
			q.push(2 * j);
		}
		if (2 *j + 1 <= h->size) {
			q.push(2 * j + 1);
		}

		
	}
}

最大堆的删除

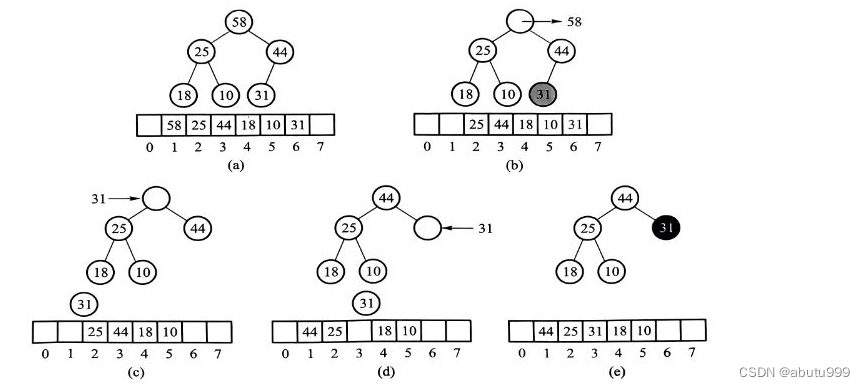
在这里插入图片描述

从根节点开始，用最大堆的最后一个元素向上过滤下层元素。

ElementType DeleteMax(Heap h) {
	if (h->size == 0) {
		printf("the heap is empty!\n");
		return -1;
	}
	else {
		int maxi = h->Data[0];//被拿走
		int x = h->Data[h->size];//要删除
		h->size--;
		int parent, child;
		for (parent = 1; 2 * parent <= h->size; parent = child) {
			child = 2 * parent;
			if (child != h->size && h->Data[child] < h->Data[child + 1]) {
				child++;
			}
			if (x >= h->Data[child]) {
				break;
			}
			else {
				h->Data[parent] = h->Data[child];
			}
		}
		h->Data[parent] = x;
		return maxi;
	}
}

最大堆的建立

将已经存在的N个元素按最大堆的要求存放在一个一维数组里。
首先，将N个元素按输入顺序插入二叉树
然后，调整各个结点元素，以满足最大堆的有序性

从第N/2结点开始，对包括该结点和该节点前面的节点进行过滤操作：对一个某一节点，当其两个子节点中较大键值的元素大于它时，将它与大键值子节点交换位置，完成一个层次的向下过滤，接着在新的层次上进行再下一层的过滤，直到找到它的正确位置。

void precDown(Heap h, int p) {
	int parent, child;
	int x = h->Data[p];
	for (parent = p; 2 * parent <= h->size; parent = child) {
		child = 2 * parent;
		if (child != 2 * parent && h->Data[child] < h->Data[child + 1]) {
			child++;
		}
		if (x >= h->Data[child]) {
			break;
		}
		else {
			h->Data[parent] = h->Data[child];
		}
	}
	h->Data[parent] = x;
}

void BulidHeap(Heap h) {
	int i;
	for (i = h->size / 2; i > 0; i--) {
		precDown(h, i);
	}
}

完整代码


#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

typedef int ElementType;
typedef struct Hnode* Heap;
struct Hnode {
	ElementType* Data;
	int size;
	int capacity;
};

//若堆里要有n个元素，则开辟的数组要有n+1大小，因为0下标位置无用，从1处开始存储
Heap CreateHeap(int maxsize) {
	Heap H = new Hnode[maxsize];
	H->capacity = maxsize ;
	H->Data = new ElementType[maxsize + 1];
	H->size = 0;
	H->Data[0] = 1e8;//定义哨兵为大于堆中所有可能元素的数值
	return H;
}
bool IsFull(Heap H) {
	if (H->size == H->capacity) {
		return true;
	}
	else {
		return false;
	}
}
bool Insert(Heap H, ElementType X) {
	//H->Data[0]为哨兵
	if (IsFull(H)) {
		printf("最大堆已满\n");
		return false;
	}

	int i = ++H->size;
	//H->Data[i/2]为其父结点 
	while (H->Data[i / 2] < X) {
		H->Data[i] = H->Data[i / 2];
		i /= 2;

	}
	H->Data[i] = X;
	return true;


}


void printh(Heap h) {
	queue<int> q;
	int i = 1;
	int j;
	q.push(i);
	while (!q.empty()) {
		j = q.front();
		printf("%d ", h->Data[j]);
		q.pop();
		if (2 * j <= h->size) {
			q.push(2 * j);
		}
		if (2 *j + 1 <= h->size) {
			q.push(2 * j + 1);
		}

		
	}
}



ElementType DeleteMax(Heap h) {
	if (h->size == 0) {
		printf("the heap is empty!\n");
		return -1;
	}
	else {
		int maxi = h->Data[0];//被拿走
		int x = h->Data[h->size];//要删除
		h->size--;
		int parent, child;
		for (parent = 1; 2 * parent <= h->size; parent = child) {
			child = 2 * parent;
			if (child != h->size && h->Data[child] < h->Data[child + 1]) {
				child++;
			}
			if (x >= h->Data[child]) {
				break;
			}
			else {
				h->Data[parent] = h->Data[child];
			}
		}
		h->Data[parent] = x;
		return maxi;
	}
}

void precDown(Heap h, int p) {
	int parent, child;
	int x = h->Data[p];
	for (parent = p; 2 * parent <= h->size; parent = child) {
		child = 2 * parent;
		if (child != 2 * parent && h->Data[child] < h->Data[child + 1]) {
			child++;
		}
		if (x >= h->Data[child]) {
			break;
		}
		else {
			h->Data[parent] = h->Data[child];
		}
	}
	h->Data[parent] = x;
}

void BulidHeap(Heap h) {
	int i;
	for (i = h->size / 2; i > 0; i--) {
		precDown(h, i);
	}
}

int main() {
	int maxsize = 10;
	Heap h = CreateHeap(maxsize);
	int n;
	cin >> n;
	int x;
	while (n--) {
		cin >> x;
		if (!Insert(h, x)) {
			printf("The heap is full!\n");
		}
	}
	printh(h);

	int mai = DeleteMax(h);
	printh(h);


	

}

STL使用

//priority_queue<int> maxheap; //默认最大堆
priority_queue<int, vector<int>, greater<int>> minheap;//最小堆
vector<int> array = { 4, 7,10,3,20,16 };
priority_queue<int> maxheap(array.begin(), array.end());
maxheap.push(11);
cout << maxheap.top() << endl;
maxheap.pop();
maxheap.pop();
cout << maxheap.top() << endl;

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1489608.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【论文阅读】Mamba:选择状态空间模型的线性时间序列建模（一）

【论文阅读】Mamba:选择状态空间模型的线性时间序列建模（一）

文章目录 Mamba:选择状态空间模型的线性时间序列建模介绍状态序列模型选择性状态空间模型动机&#xff1a;选择作为一种压缩手段用选择性提升SSM 选择性SSM的高效实现先前模型的动机选择扫描总览&#xff1a;硬件感知状态扩展 Mamba论文 Mamba:选择状态空间模型的线性时间序列建…
阅读更多...
【.NET Core】深入理解IO - 读取器和编写器

【.NET Core】深入理解IO - 读取器和编写器

【.NET Core】深入理解IO - 读取器和编写器 文章目录 【.NET Core】深入理解IO - 读取器和编写器一、概述二、BinaryReader和BinaryWriter2.1 BinartReader类2.2 BinaryWriter类 三、StreamReader和StreamWriter3.1 StreamReader类3.1 StreamWriter类StreamWriter类构造函数Str…
阅读更多...
AI大语言模型【成像光谱遥感技术】ChatGPT应用指南

AI大语言模型【成像光谱遥感技术】ChatGPT应用指南

遥感技术主要通过卫星和飞机从远处观察和测量我们的环境&#xff0c;是理解和监测地球物理、化学和生物系统的基石。ChatGPT是由OpenAI开发的最先进的语言模型&#xff0c;在理解和生成人类语言方面表现出了非凡的能力。本文重点介绍ChatGPT在遥感中的应用&#xff0c;人工智能…
阅读更多...
想学习FPGA，建议购买哪一款开发板呢？

想学习FPGA，建议购买哪一款开发板呢？

FPGA项目&#xff1a; 多通道信号采集呈像系统 该系统是以Artix-7系列的FPGA为主控芯片&#xff0c;设计并实现了一款基于A7系列开发板的多通道信号采集呈像系统&#xff0c;该设计采用DAC芯片&#xff08;数模转换芯片&#xff09;将数字信号转换成模拟信号&#xff0c;通过…
阅读更多...
LLM春招，搜广推，nlp(2)

LLM春招，搜广推，nlp(2)

Encoder和Decoder怎么交互的 decoder里面的K&#xff0c;V输入用的是encoder的输出&#xff0c;并不是共享了K, V参数&#xff0c;decoder每层的参数都是独立的。Decoder每层是有两块Attention的&#xff1a;一块是正常的Self-Attention&#xff0c;QKV的输入都来自Decoder上一…
阅读更多...
ArcGIS学习（九）选址分析

ArcGIS学习（九）选址分析

ArcGIS学习（九）选址分析 本任务给大家带来的案例是租房选址分析。选址分析是我们平时经常接触到的分析场景。概括起来说，选址分析就是根据选址条件来确定哪些区域满足我们的选址要求。首先，先来看看我们这个案例的场景和基础数据。我们以某个城市某一租客的租房选址为例。…
阅读更多...
STM32CubeMX学习笔记8 -ADC

STM32CubeMX学习笔记8 -ADC

1. ADC简介 ADC 是Analog-to-Digital Converter的缩写。指模/数转换器或者模拟/数字转换器。是指将连续变量的模拟信号转换为离散的数字信号的器件。典型的模拟数字转换器将模拟信号转换为表示一定比例电压值的数字信号。简单地说就是将模拟电压值&#xff0c;转换成对应的肉眼…
阅读更多...
完结撒花~Matlab论文插图绘制模板第139期—罗盘图

完结撒花~Matlab论文插图绘制模板第139期—罗盘图

2021年2月2日&#xff0c;Matlab论文插图绘制模板第1期&#xff0c;启动。 三年后…… 2024年3月4日&#xff0c;Matlab论文插图绘制模板第139期&#xff0c;完结。 别的也不多说了&#xff0c;《Matlab论文插图绘制模板》1-139期精修合集&#xff0c;正加速整理制作中&…
阅读更多...
7款炫酷的前端动画特效分享（三）（附效果图及在线演示）

7款炫酷的前端动画特效分享（三）（附效果图及在线演示）

分享7款好玩的前端动画特效 其中有CSS动画、SVG动画、js小游戏等等 下方效果图可能不是特别的生动 那么你可以点击在线预览进行查看相应的动画特效 同时也是可以下载该资源的 CSS3模仿四季交替动画 基于HTML5CSS3实现的卡通风格一年四季交替动画特效 以下效果图只能体现框架的…
阅读更多...
mac下终端命令提示补全

mac下终端命令提示补全

欢迎来到我的博客&#xff0c;代码的世界里&#xff0c;每一行都是一个故事 mac下终端命令提示补全 前言Zsh-autosuggestions原理解析&#xff1a;智能提示的工作方式1. 命令历史分析&#xff1a;2. 智能提示生成&#xff1a;3. 用户交互和选择&#xff1a;4. 配置和个性化&…
阅读更多...
Java集合框架-Collection和Map

Java集合框架-Collection和Map

文章目录 Collection-单列集合特点ListArrayListLinkedListVecter SetHashSetTreeSet Map-键值对集合特点Map常用APIput添加细节remove Map的三种遍历方式1.通过键找值2.通过"键值对"3.Lambda表达式foreach源码 HashMap需求 为什么要使用泛型 泛型的优点1.集合中存储…
阅读更多...
《精益DevOps》译者序

《精益DevOps》译者序

计算机网络的发展导致了IT领域中的两个重要发展——虚拟化和分布式计算&#xff0c;云服务是虚拟化的一个直接体现&#xff0c;而微服务架构则是分布式计算的一个重要应用领域。不论是虚拟化还是分布式计算&#xff0c;都对软件工程中的研发效能提出了新的问题和挑战&#xff0…
阅读更多...
Linux x86平台获取sys_call_table

Linux x86平台获取sys_call_table

文章目录 前言一、根据call *sys_call_table来获取二、使用dump_stack三、根据MSR_LSTAR寄存器四、使用sys_close参考资料 前言 Linux 3.10.0 – x86_64 最简单获取sys_call_table符号的方法&#xff1a; # cat /proc/kallsyms | grep sys_call_table ffffffff816beee0 R sy…
阅读更多...
实名制交友-智能匹配-仿二狗交友系统-TP6+uni-APP小程序H5公众号-源码交付-支持二开！

实名制交友-智能匹配-仿二狗交友系统-TP6+uni-APP小程序H5公众号-源码交付-支持二开！

一、代码风格 通常不同的开发者具备不同的代码风格&#xff0c;但为了保证语音交友系统开发质量&#xff0c;在编码前需要进行代码风格的统一&#xff0c;通过制定一定的规则&#xff0c;约束开发者的行为。具有统一风格的代码才能更清晰、更完整、更容易理解、更方便后期维护…
阅读更多...
互联网加竞赛 车道线检测(自动驾驶 机器视觉)

互联网加竞赛 车道线检测(自动驾驶 机器视觉)

0 前言 无人驾驶技术是机器学习为主的一门前沿领域&#xff0c;在无人驾驶领域中机器学习的各种算法随处可见&#xff0c;今天学长给大家介绍无人驾驶技术中的车道线检测。 1 车道线检测 在无人驾驶领域每一个任务都是相当复杂&#xff0c;看上去无从下手。那么面对这样极其…
阅读更多...
AURIX CSA(上下文存储)介绍（续写中...）

AURIX CSA(上下文存储)介绍（续写中...）

1.CSA概述 CSA&#xff08;Context Save Areas&#xff09;上下文存储区域&#xff0c;每次函数调用、进入中断、进入Trap都会存CSA对象&#xff0c;便于退出时候恢复。每个CSA对象的大小为固定的64字节。最大可以支持分配为2^164M。 2.GPRs寄存器 32个通用寄存器(GPRs) 16个…
阅读更多...
Redis缓存【重点】

Redis缓存【重点】

参考链接 https://xiaolincoding.com/redis/cluster/cache_problem.html#%E7%BC%93%E5%AD%98%E9%9B%AA%E5%B4%A9 目录 缓存雪崩大量数据同时过期Redis 故障宕机 缓存击穿第一种方案&#xff0c;非法请求的限制第二种方案&#xff0c;缓存空值或者默认值第三种方案&#xff0c;使…
阅读更多...
回溯算法套路②组合型回溯+剪枝【基础算法精讲 15】

回溯算法套路②组合型回溯+剪枝【基础算法精讲 15】

学习地址 : 回溯算法套路②组合型回溯剪枝【基础算法精讲 15】_哔哩哔哩_bilibili 回顾 &#xff1a; 从n 个数中选出k个数的组合 &#xff0c; 可以看成是长度固定的子集 ; 剪枝技巧 : 77 . 组合 链接 : . - 力扣&#xff08;LeetCode&#xff09; 枚举下一个元素选…
阅读更多...
嵌入式中volatile关键字的使用方法

嵌入式中volatile关键字的使用方法

Hi,大家好&#xff01; 今天我们来学习一下volatile关键字&#xff0c;volatile关键字想必大家在平时编程中都见过或用过。可是小伙伴们有没有想过什么时候需要使用volatile关键字吗&#xff1f; 在C语言中&#xff0c;volatile是一个关键字&#xff0c;用于告诉编译器不要优化…
阅读更多...
【MATLAB第97期】基于MATLAB的贝叶斯Bayes算法优化BiGRU双向门控循环单元的多输入单输出回归预测模型，含GRU与BiGRU多层结构优化选择

【MATLAB第97期】基于MATLAB的贝叶斯Bayes算法优化BiGRU双向门控循环单元的多输入单输出回归预测模型，含GRU与BiGRU多层结构优化选择

【MATLAB第97期】基于MATLAB的贝叶斯Bayes算法优化BiGRU双向门控循环单元的多输入单输出回归预测模型&#xff0c;含GRU与BiGRU结构层数优化 前言 前面在【MATLAB第10期】讲解了基于贝叶斯Bayes算法优化LSTM长短期记忆网络的多输入单输出回归预测模型。 本次模型难点包括&am…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023