【MATLAB第97期】基于MATLAB的贝叶斯Bayes算法优化BiGRU双向门控循环单元的多输入单输出回归预测模型,含GRU与BiGRU结构层数优化
前言
前面在【MATLAB第10期】讲解了基于贝叶斯Bayes算法优化LSTM长短期记忆网络的多输入单输出回归预测模型。
本次模型难点包括:
1、BiGRU模型代码的编制
2、多层BiGRU模型代码的编制
3、BO-BiGRU模型代码的编制
数据
7输入1输出
%% 导入数据(时间序列的单列数据)
result = xlsread('data.xlsx');
%% 数据分析
num_samples = length(result); % 样本个数
kim = 7; % 延时步长(kim个历史数据作为自变量)
zim = 1; % 跨zim个时间点进行预测
%% 构造数据集
for i = 1: num_samples - kim - zim + 1
res(i, :) = [reshape(result(i: i + kim - 1), 1, kim), result(i + kim + zim - 1)];
end
%% 划分训练集和测试集
temp = 1: 1: 922;
P_train = res(temp(1: 700), 1: 7)';
T_train = res(temp(1: 700), 8)';
M = size(P_train, 2);
P_test = res(temp(701: end), 1: 7)';
T_test = res(temp(701: end), 8)';
N = size(P_test, 2);
%% 数据归一化
[P_train, ps_input] = mapminmax(P_train, 0, 1);
P_test = mapminmax('apply', P_test, ps_input);
[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);
%% 数据平铺
% 将数据平铺成1维数据只是一种处理方式
% 也可以平铺成2维数据,以及3维数据,需要修改对应模型结构
% 但是应该始终和输入层数据结构保持一致
P_train = double(reshape(P_train, 7, 1, 1, M));
P_test = double(reshape(P_test , 7, 1, 1, N));
t_train = t_train';
t_test = t_test' ;
%% 数据格式转换
for i = 1 : M
p_train{i, 1} = P_train(:, :, 1, i);
end
for i = 1 : N
p_test{i, 1} = P_test( :, :, 1, i);
end
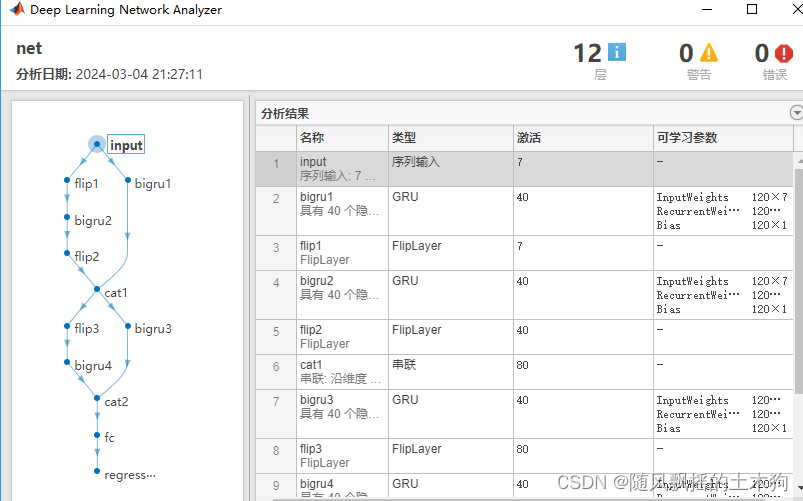
%% 创建模型
inputSize = 7; % 输入特征个数
numResponses = 1; % 输出特征个数
NumOfUnits = 40; % 隐含层神经元个数
layers = layerGraph();
%% 参数设置
options = trainingOptions('adam', ... % Adam 梯度下降算法
'MiniBatchSize', 50, ... % 批大小
'MaxEpochs', 100, ... % 最大迭代次数
'InitialLearnRate', 1e-2, ... % 初始学习率为
'LearnRateSchedule', 'piecewise', ... % 学习率下降
'LearnRateDropFactor', 0.5, ... % 学习率下降因子
'LearnRateDropPeriod', 50, ... % 经过 500 次训练后 学习率为 0.01 * 0.5
'Shuffle', 'every-epoch', ... % 每次训练打乱数据集
'Plots', 'training-progress', ... % 画出曲线
'Verbose', false);
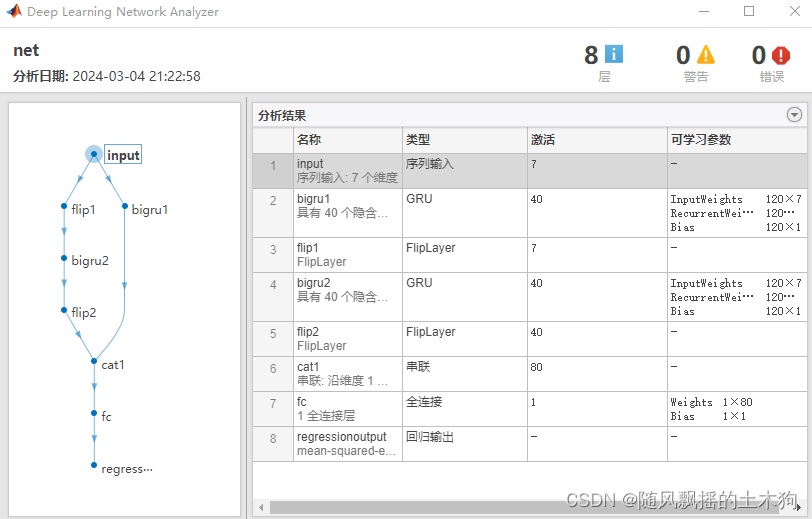
一、单层BiGRU
参考链接:
BIGRU(Bidirectional Gated Recurrent Unit)是一种基于双向门控循环单元(GRU)的多变量时间序列预测方法。它结合了双向模型和门控机制,能够有效地捕捉时间序列数据中的时序关系和多变量之间的相互影响。
GRU是一种循环神经网络(RNN)的变体,相比于传统的循环神经网络(如LSTM),GRU具有更少的参数和计算复杂度。它通过引入门控单元来控制信息的流动,从而在处理长期依赖关系时具有更好的性能。
BIGRU模型由两个方向的GRU网络组成,一个网络从前向后处理时间序列数据,另一个网络从后向前处理时间序列数据。这种双向结构可以同时捕捉到过去和未来的信息,从而更全面地建模时间序列数据中的时序关系。
在BIGRU模型中,每个GRU单元都有更新门和重置门来控制信息的流动。更新门决定了当前时刻的输入是否对当前状态进行更新,而重置门决定了如何将过去的状态与当前输入结合起来。通过这些门控机制,BIGRU模型可以自适应地学习时间序列数据中的长期依赖关系和多变量之间的相互影响。
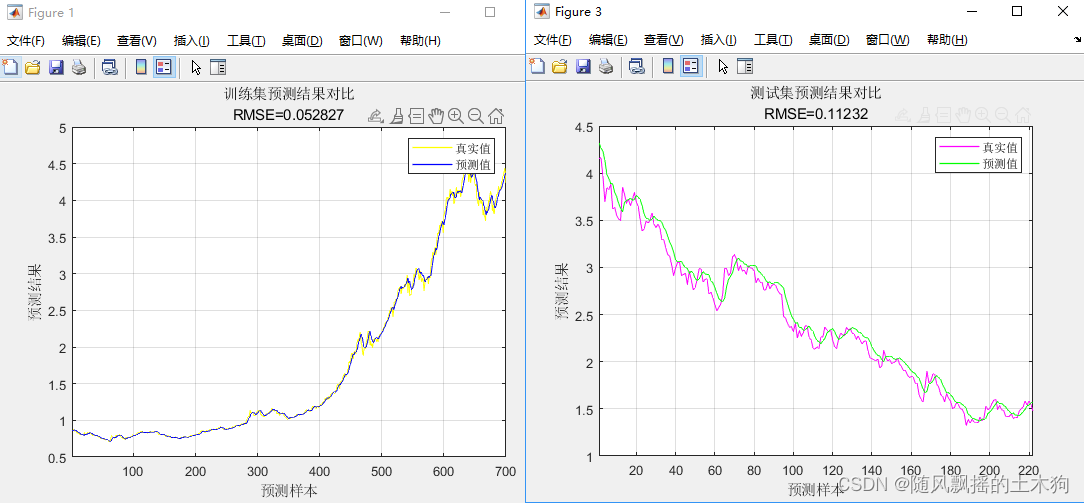
训练集数据的MAPE为:0.015984
测试集数据的MAPE为:0.037648
训练集数据的RMSE为:0.052827
测试集数据的RMSE为:0.11232
训练集数据的R2为:0.99808
测试集数据的R2为:0.97666
训练集数据的MAE为:0.032269
测试集数据的MAE为:0.088781
训练集数据的MBE为:-0.0040228
测试集数据的MBE为:0.057725
二、多层BiGRU
1.双层
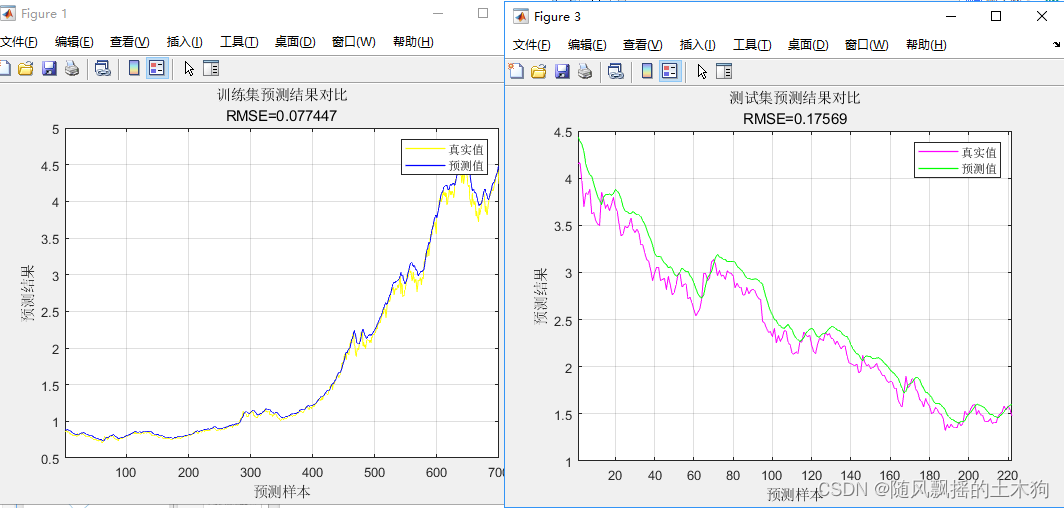
训练集数据的MAPE为:0.025075
测试集数据的MAPE为:0.060946
训练集数据的RMSE为:0.077447
测试集数据的RMSE为:0.17569
训练集数据的R2为:0.99587
测试集数据的R2为:0.94288
训练集数据的MAE为:0.047427
测试集数据的MAE为:0.14756
训练集数据的MBE为:0.041614
测试集数据的MBE为:0.13522
2.三层
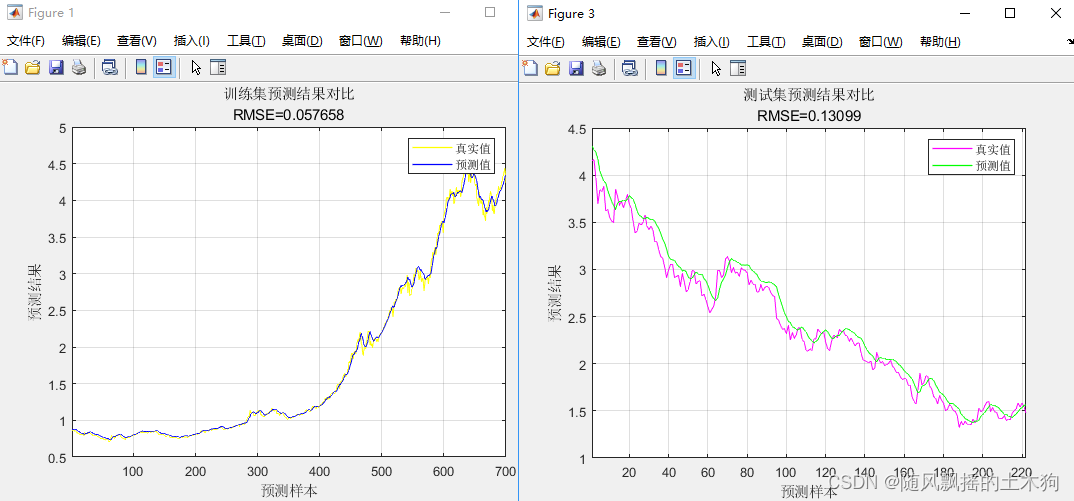
训练集数据的MAPE为:0.019441
测试集数据的MAPE为:0.045008
训练集数据的RMSE为:0.057658
测试集数据的RMSE为:0.13099
训练集数据的R2为:0.99771
测试集数据的R2为:0.96825
训练集数据的MAE为:0.036483
测试集数据的MAE为:0.10681
训练集数据的MBE为:0.0048439
测试集数据的MBE为:0.079081
3.四层
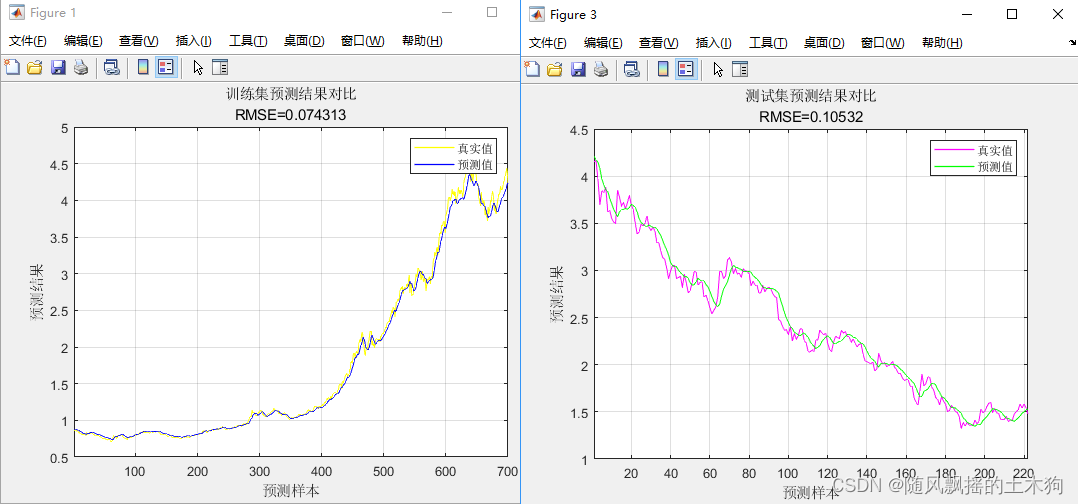
训练集数据的MAPE为:0.023143
测试集数据的MAPE为:0.034958
训练集数据的RMSE为:0.074313
测试集数据的RMSE为:0.10532
训练集数据的R2为:0.9962
测试集数据的R2为:0.97947
训练集数据的MAE为:0.047467
测试集数据的MAE为:0.081923
训练集数据的MBE为:-0.026566
测试集数据的MBE为:0.028198
三、BO-BiGRU(含多层BiGRU)
clc; clear; close all;
%% -------------- 初始化变量 ------ ----------
%opt.Delays = 1:10;%数据滞后30=滑动窗口
%opt.dataPreprocessMode为数据预处理,'None'代表无处理,'Data Standardization'代表标准化处理,
%'Data Normalization'代表归一化处理
opt.dataPreprocessMode = 'Data Normalization'; %三种数据处理方式 'None' 'Data Standardization' 'Data Normalization'
opt.learningMethod = 'GRU';%选择GRU作为训练模型
opt.trPercentage = 0.76; % 将数据划分为测试和训练数据集,0.76代表训练集比例
%----通用深度学习参数(GRU和CNN通用参数)
opt.maxEpochs = 100; %400 % 深度学习算法中最大训练次数。
opt.miniBatchSize = 50; % 深度学习算法中的样本最小批处理数量大小。
opt.executionEnvironment = 'cpu'; % 运行环境 'cpu' 'gpu' 'auto'
opt.LR = 'adam'; %GRU学习函数 'sgdm' 'rmsprop' 'adam'
opt.trainingProgress = 'none'; %是否运行训练图 'training-progress' 'none'
% ------------- BIGRU参数
opt.isUseBiGRULayer = true; % 如果为true,则为双向 GRU,如果为false,则转为单向GRU
opt.isUseDropoutLayer = true; % dropout 层避免过拟合
opt.DropoutValue = 0.5; % dropout 层概率为0.5
% ------------ 优化参数
opt.optimVars = [
optimizableVariable('NumOfLayer',[1 4],'Type','integer') %优化GRU隐含层层数(1-4) ,层数数据类型为整数
optimizableVariable('NumOfUnits',[20 200],'Type','integer')%优化GRU隐含层神经元(50-200) ,数据类型为整数
optimizableVariable('isUseBiGRULayer',[1 2],'Type','integer')%优化GRU结构,1代表BiGRU,2代表GRU, ,数据类型为整数
optimizableVariable('InitialLearnRate',[1e-2 1],'Transform','log')%优化GRU初始学习率(0.01-1) ,数据类型为浮点型
optimizableVariable('L2Regularization',[1e-10 1e-2],'Transform','log')];%优化GRU正则化L2系数(1e-10-1e-2) ,数据类型为浮点型
opt.isUseOptimizer = true;%是否选择贝叶斯优化
opt.MaxOptimizationTime = 14*60*20;%优化运行的最大时间14*60*60
opt.MaxItrationNumber = 30;%优化运行的最大迭代次数60
opt.isDispOptimizationLog = true;%是否展示优化过程日志
opt.isSaveOptimizedValue = false; % 是否将所有优化输出保存在 mat 文件中
opt.isSaveBestOptimizedValue = true; % 是否将最佳优化输出保存为 mat 文件
%% --------------- 加载数据
data = loadData(opt);
if ~data.isDataRead
return;
end
%% --------------- 准备数据
[opt,data] = PrepareData(opt,data);
%% --------------- 使用贝叶斯优化找到最佳 GRU 参数
[opt,data] = OptimizeGRU(opt,data);
%% --------------- 评估数据
[opt,data] = EvaluationData(opt,data);
save result_BO-BiGRU
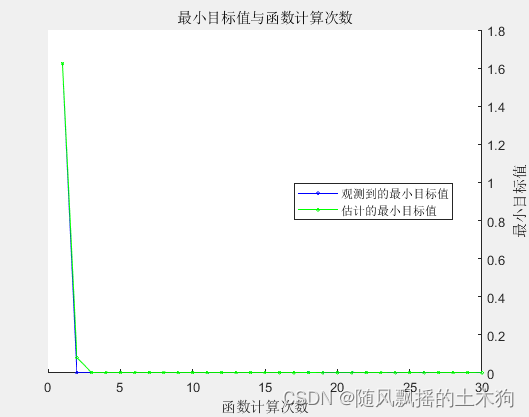
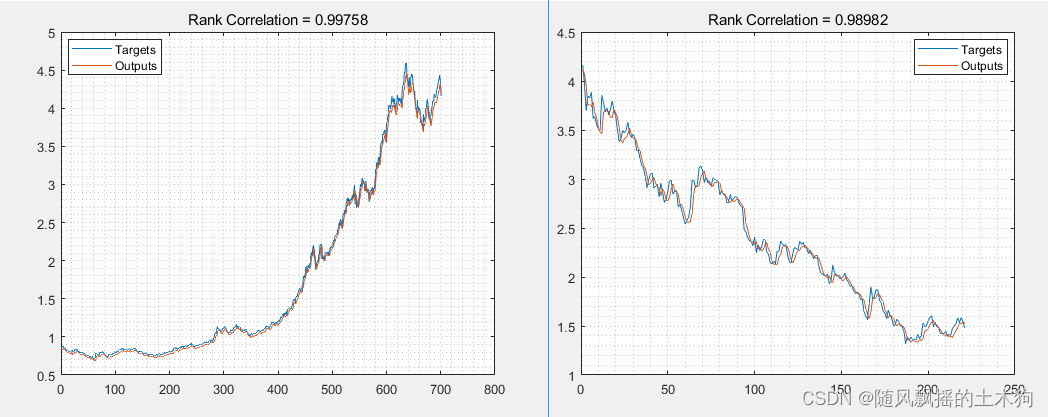
测试集R2: 0.98962
训练集R2:0.99758
运行过程结果:
达到 MaxObjectiveEvaluations 30。
函数计算总次数: 30
总历时: 945.2992 秒。
总目标函数计算时间: 905.6441
观测到的最佳可行点:
NumOfLayer NumOfUnits isUseBiGRULayer InitialLearnRate L2Regularization
1.00 199.00 2.00 0.01 0.00
观测到的目标函数值 = 0.0017557
估计的目标函数值 = 0.0015089
函数计算时间 = 21.0219
估计的最佳可行点(根据模型):
NumOfLayer NumOfUnits isUseBiGRULayer InitialLearnRate L2Regularization
1.00 199.00 2.00 0.01 0.00
估计的目标函数值 = 0.0015089
估计的函数计算时间 = 21.0541

四、结论
针对本案例数据,1-4层BiGRU回归模型测试时, 1层结构与4层结构拟合结果较好,但因4层结构运行速度慢,结构复杂,加上数据量少,所以在本案例中不太适用。
贝叶斯优化BiGRU模型中,30次迭代后最佳的结构是单层GRU结构,但与单层BiGRU结果相差不大,具有一定的可行性。
再严谨一点儿,需要把30次迭代最优结构结果进行分析,判断BiGRU相对于GRU的优势或者劣势,至少从运行结果可知,BiGRU下限很低,所以不推荐使用默认参数,而需要搭配进化算法进行使用。GRU结构相对较为稳定,但内容比较单一,相比LSTM没有明显优势。
以上,若用BiGRU,使用一层结构的就足够了(结论不严谨,仅针对本次案例)。
五、代码获取
1.阅读首页置顶文章
2.关注CSDN
3.根据自动回复消息,回复“96期”以及相应指令,即可获取对应下载方式。
![[linux]shell脚本语言:变量、测试、控制语句以及函数的全面详解](https://img-blog.csdnimg.cn/76b6806d36ed47b2a145cb9bf9e78dc9.png)