学习地址 : 

回溯算法套路②组合型回溯+剪枝【基础算法精讲 15】_哔哩哔哩_bilibili

回顾 ： 

从n 个数中选出k个数的组合 ， 可以看成是长度固定的子集 ;

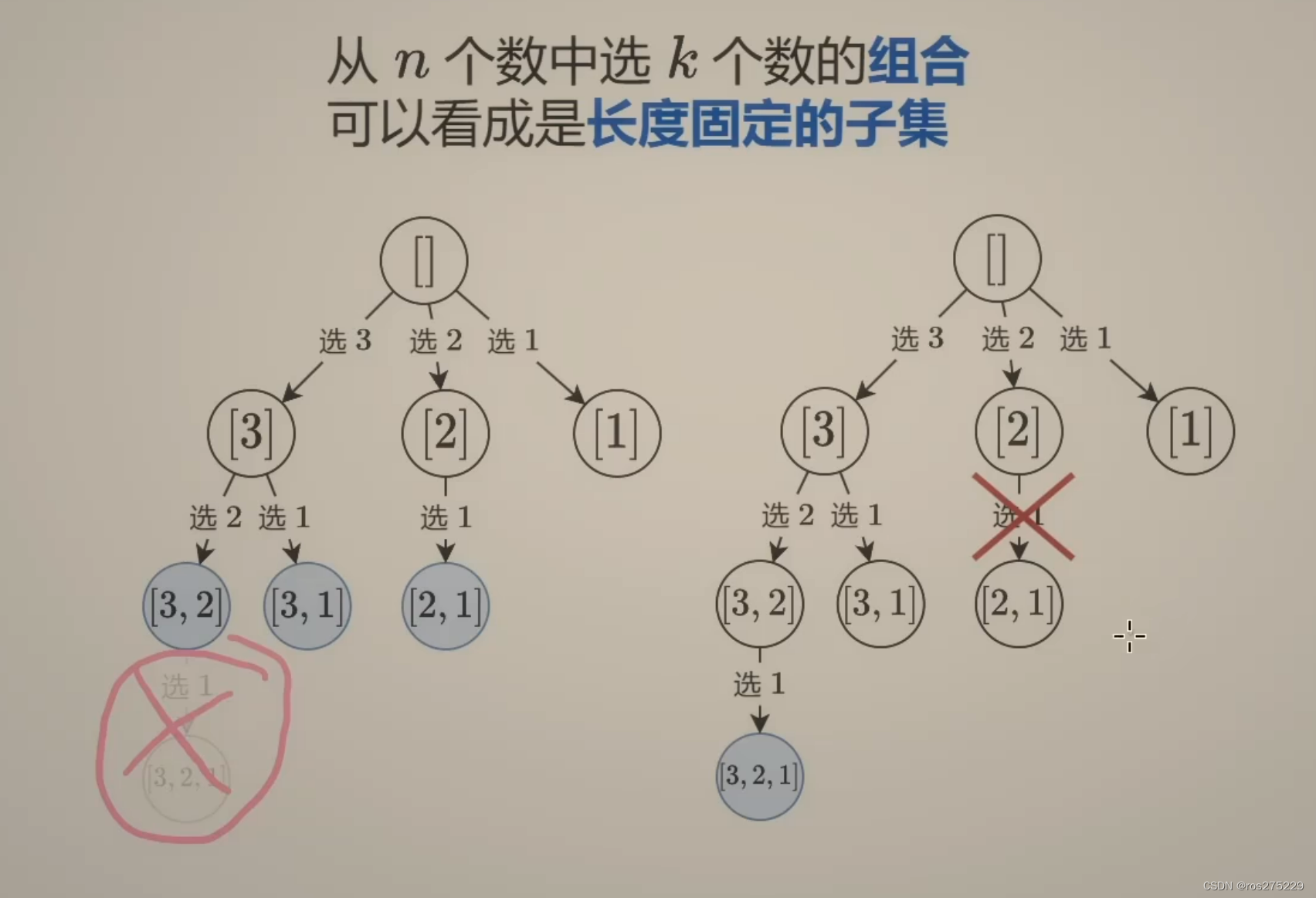
 剪枝技巧 : 

 77 . 组合 

链接 : 

. - 力扣（LeetCode）

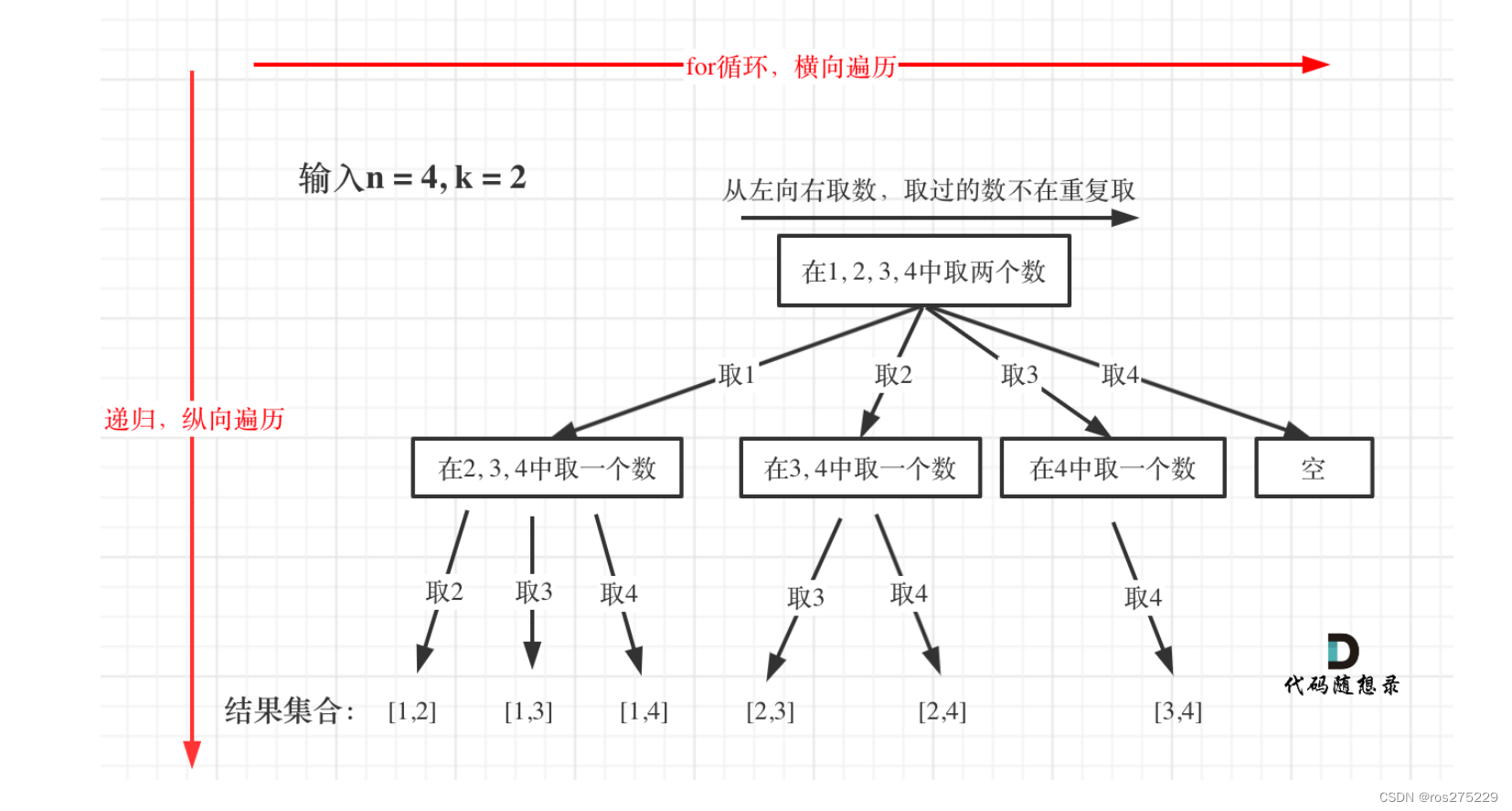
枚举下一个元素选谁: 

回溯;

void dfs(int n , int k , int idx) ;

idx确定选取元素不重复 ;

如果当前集合中元素个数==k , 那么加入到ans中 ；

枚举下 一 个数选谁 ，从idx开使 ， 遍历到n ; 

class Solution {
public:
    vector<vector<int>> ans  ;
    vector<int> path ;

    void dfs(int n , int k , int idx){
        if(path.size() == k){
            ans.push_back(path) ;
            return  ; // 回溯
        }
        for(int i=idx;i<=n;i++){// 找下一个选谁
            path.push_back(i) ;
            dfs(n,k,i+1) ;
            path.pop_back() ;
        }
    }

    vector<vector<int>> combine(int n, int k) {
        dfs(n , k , 1);
        return ans ;
    }
};

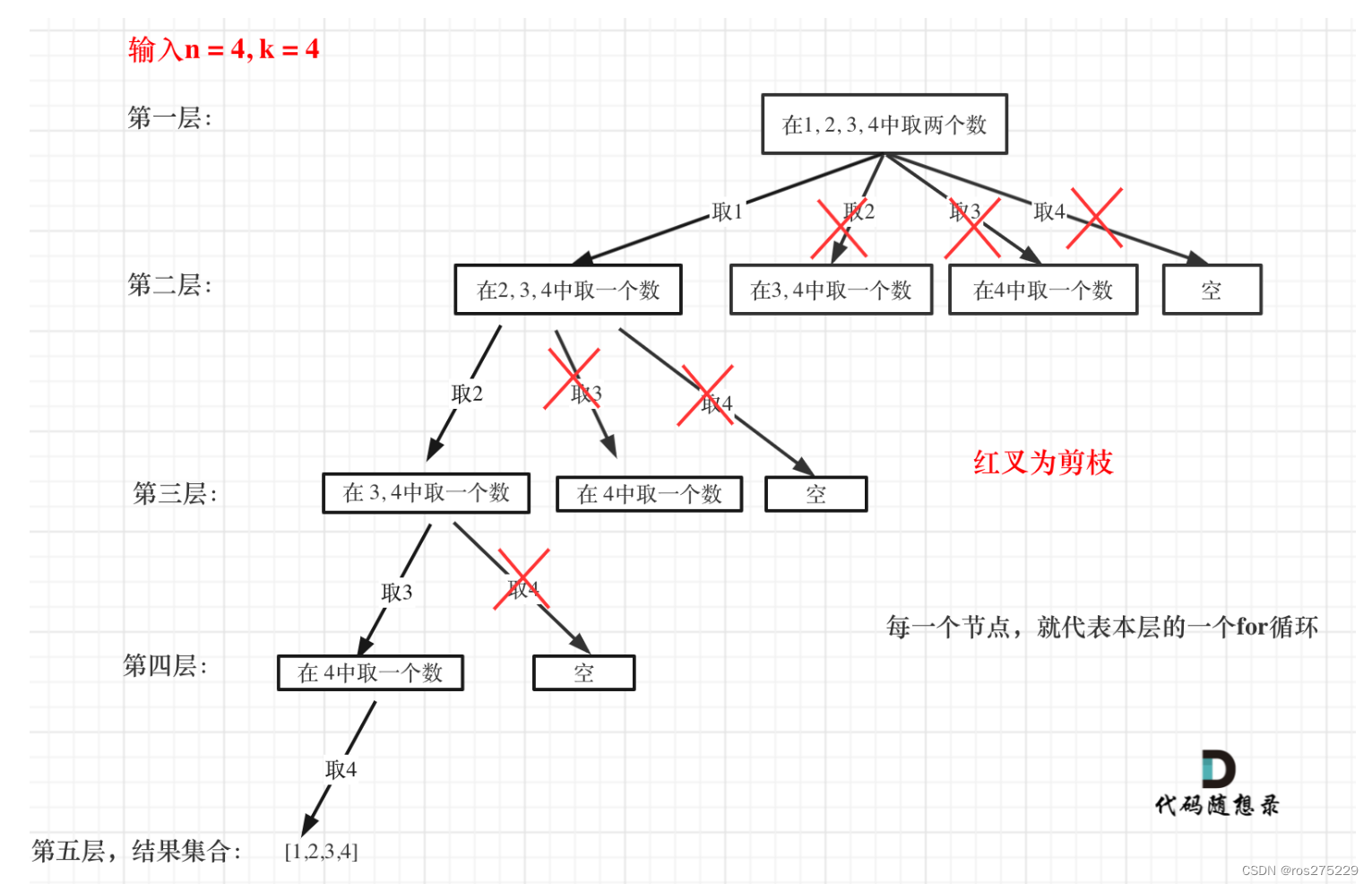
剪枝优化版本 : 

剪枝示意图 : 

class Solution {
public:
    vector<vector<int>> ans  ;
    vector<int> path ;

    void dfs(int n , int k , int idx){
        int sz = path.size() ;
        if(sz == k){
            ans.push_back(path) ;
            return  ; // 回溯
        }
        // 后面还有 n-idx 个元素 , 还要选 k - sz 个元素
        if(k-sz > n-idx+1) return ;

        for(int i=idx;i<=n;i++){// 找下一个选谁
            path.push_back(i) ;
            dfs(n,k,i+1) ;
            path.pop_back() ;
        }
    }

    vector<vector<int>> combine(int n, int k) {
        dfs(n , k , 1);
        return ans ;
    }
};

选或不选的思路 : 

这个一定要剪枝优化一下 ， 否者会超时 ;

class Solution {
public:
    vector<vector<int>> ans  ;
    vector<int> path ;

    void dfs(int n , int k , int idx){
        int sz = path.size() ;
        if(sz == k){
            ans.push_back(path) ;
            return  ; // 回溯
        }

        if(k-sz>n-idx+1) return ;

        // 不选 
        dfs(n,k,idx+1) ;

        // 选
        path.push_back(idx) ;
        dfs(n,k,idx+1) ;
        path.pop_back() ;
    }

    vector<vector<int>> combine(int n, int k) {
        dfs(n , k , 1);
        return ans ;
    }
};

216 . 组合总和 III

链接 : 

. - 力扣（LeetCode）

思路 : 

在找到k个元素之后 ， 判断当前元素和是不是等于 k , 如果是 ， 加入答案数组 ；

class Solution {
private:
    vector<vector<int>> result; // 存放结果集
    vector<int> path; // 符合条件的结果
    // targetSum：目标和，也就是题目中的n。
    // k：题目中要求k个数的集合。
    // sum：已经收集的元素的总和，也就是path里元素的总和。
    // startIndex：下一层for循环搜索的起始位置。
    void backtracking(int targetSum, int k, int sum, int startIndex) {
        if (path.size() == k) {
            if (sum == targetSum) result.push_back(path);
            return; // 如果path.size() == k 但sum != targetSum 直接返回
        }
        for (int i = startIndex; i <= 9; i++) {
            sum += i; // 处理
            path.push_back(i); // 处理
            backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndex
            sum -= i; // 回溯
            path.pop_back(); // 回溯
        }
    }

public:
    vector<vector<int>> combinationSum3(int k, int n) {
        result.clear(); // 可以不加
        path.clear();   // 可以不加
        backtracking(n, k, 0, 1);
        return result;
    }
};

剪枝 : 

class Solution {
private:
    vector<vector<int>> result; // 存放结果集
    vector<int> path; // 符合条件的结果
    void backtracking(int targetSum, int k, int sum, int startIndex) {
        if (sum > targetSum) { // 剪枝操作
            return; 
        }
        if (path.size() == k) {
            if (sum == targetSum) result.push_back(path);
            return; // 如果path.size() == k 但sum != targetSum 直接返回
        }
        for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) { // 剪枝
            sum += i; // 处理
            path.push_back(i); // 处理
            backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndex
            sum -= i; // 回溯
            path.pop_back(); // 回溯
        }
    }

public:
    vector<vector<int>> combinationSum3(int k, int n) {
        result.clear(); // 可以不加
        path.clear();   // 可以不加
        backtracking(n, k, 0, 1);
        return result;
    }
};

22 . 括号生成

链接 : 

. - 力扣（LeetCode）

思路 : 

选或不选 : 

 

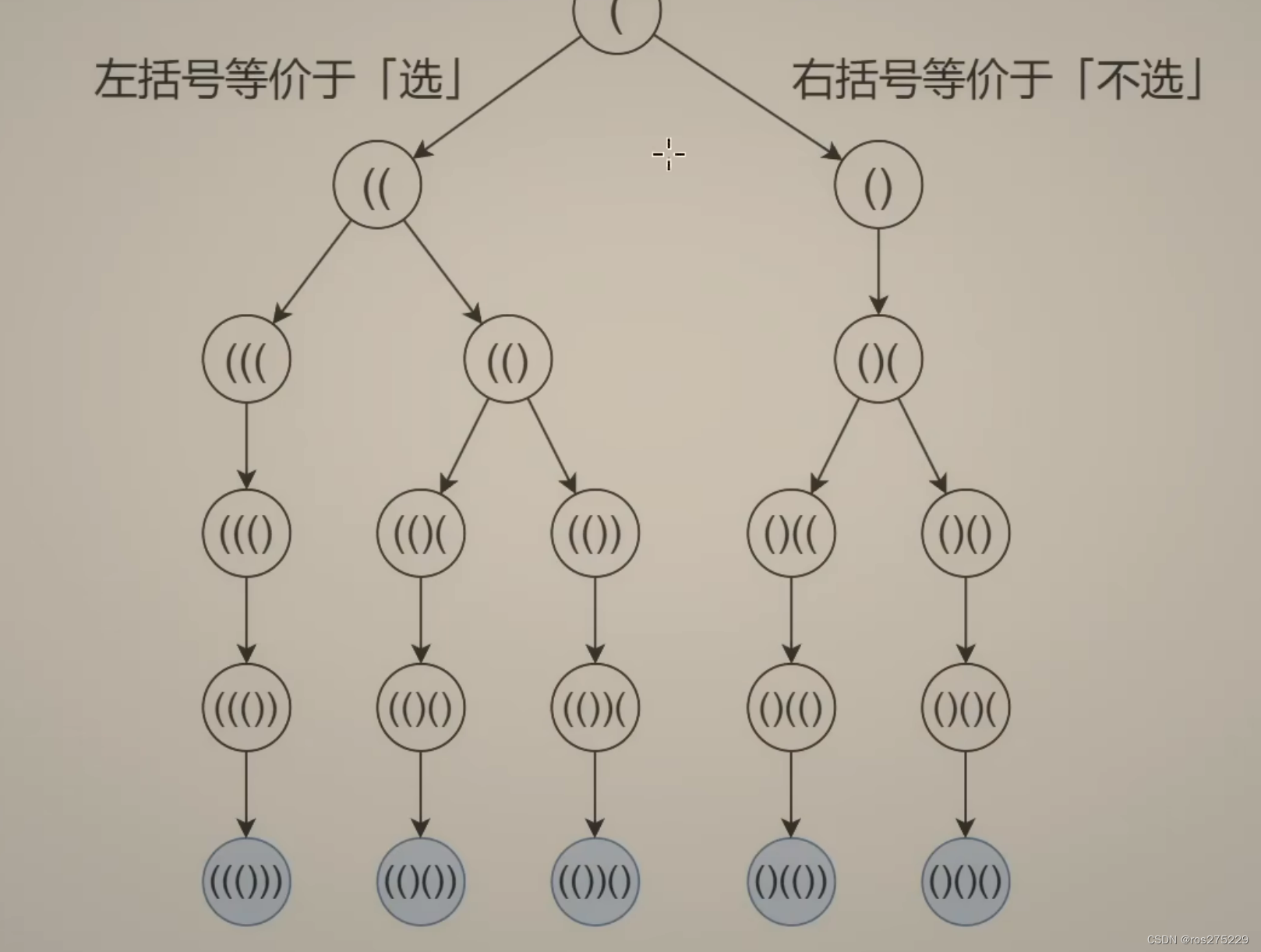
直接暴力 : 

选2*n个左右括号 ， 对得到每个左右括号序列进行判断 ， 共有2 ^(2*n)种可能 ，如果是有效的 ， 那么加入到ans 中 ; 

class Solution {
public:
    bool pd(const string& s){
        int t = 0 ;
        for(char c : s){
            if(c=='(') t++;
            else --t;
            if(t<0) return false;
        }
        return t==0 ;
    }

    vector<string> ans ;

    void hs(string& s,int n){
        if(s.size()==n) {
            if(pd(s)) ans.push_back(s) ;
            return ;
        }
        // 加左括号
        s+='(';
        hs(s,n);
        s.pop_back();
        // 加右括号
        s+=')';
        hs(s,n);
        s.pop_back();
    }

    vector<string> generateParenthesis(int n) {
        string tmp = "" ;
        hs(tmp,n*2);
        return ans ;
    }
};

枚举填左括号还是右括号 ;

class Solution {
public:
    vector<string> generateParenthesis(int n) {
        int m = n * 2;
        vector<string> ans;
        string path(m, 0);
        function<void(int, int)> dfs = [&](int i, int open) {
            if (i == m) {
                ans.emplace_back(path);
                return;
            }
            if (open < n) { // 可以填左括号
                path[i] = '(';
                dfs(i + 1, open + 1);
            }
            if (i - open < open) { // 可以填右括号
                path[i] = ')';
                dfs(i + 1, open);
            }
        };
        dfs(0, 0);
        return ans;
    }
};