yolov7添加spd-conv注意力机制

news2024/9/22 15:46:04

一、spd-conv是什么？

SPD-Conv（Symmetric Positive Definite Convolution）是一种新颖的卷积操作，它主要应用于处理对称正定矩阵（SPD）数据。在传统的卷积神经网络（CNN）中，卷积操作通常用于处理图像数据，而SPD-Conv的引入则将卷积扩展到了处理更加复杂的数据结构，例如在计算机视觉、医学影像分析和材料科学等领域中广泛存在的对称正定矩阵数据。

1.SPD矩阵的特点

对称正定矩阵是一类特殊的矩阵，具有严格的数学定义，通常表示为X∈Rn×nX∈Rn×n，其中 XX 是对称正定矩阵，满足 XT=XXT=X 和对于任意非零向量 vv，有 vTXv>0vTXv>0。这种矩阵广泛应用于协方差矩阵、距离度量、流形学习等领域，并且在一些任务中，数据被表示为SPD矩阵，例如医学图像的核磁共振（MRI）图像。

2.SPD-Conv的引入

SPD-Conv是针对SPD数据设计的卷积操作。与传统的卷积操作不同，SPD-Conv考虑了SPD矩阵的特殊结构和性质。它在对SPD数据进行卷积时，保持了输入和输出的对称正定性，确保了卷积结果仍然是对称正定矩阵。这种特性使得SPD-Conv适用于处理一些需要保持数据结构特性的任务，例如在医学影像中保持图像的对称性和正定性。
SPD-Conv是一种新的构建块，用于替代现有的CNN体系结构中的步长卷积和池化层。它由一个空间到深度(SPD)层和一个非步长卷积(Conv)层组成。
空间到深度（SPD）层的作用是将输入特征图的每个空间维度降低到通道维度，同时保留通道内的信息。这可以通过将输入特征图的每个像素或特征映射到一个通道来实现。在这个过程中，空间维度的大小会减小，而通道维度的大小会增加。
非步长卷积(Conv)层是一种标准的卷积操作，它在SPD层之后进行。与步长卷积不同，非步长卷积不会在特征图上移动，而是对每个像素或特征映射进行卷积操作。这有助于减少在SPD层中可能出现的过度下采样问题，并保留更多的细粒度信息。
SPD-Conv的组合方式是将SPD层和Conv层串联起来。具体来说，输入特征图首先通过SPD层进行转换，然后输出结果再通过Conv层进行卷积操作。这种组合方式可以在不丢失信息的情况下减少空间维度的尺寸，同时保留通道内的信息，有助于提高CNN对低分辨率图像和小型物体的检测性能。

总结起来，SPD-Conv是一种新的构建块，旨在解决现有CNN体系结构中步长卷积和池化层的问题。它由一个空间到深度(SPD)层和一个非步长卷积(Conv)层组成，能够提高模型对低分辨率图像和小型物体的检测性能，并降低对“良好质量"输入的依赖。

二、使用步骤

1.第一步：先在models/common.py加上


class space_to_depth(nn.Module):
    # Changing the dimension of the Tensor
    def __init__(self, dimension=1):
        super().__init__()
        self.d = dimension

    def forward(self, x):
         return torch.cat([x[..., ::2, ::2], x[..., 1::2, ::2], x[..., ::2, 1::2], x[..., 1::2, 1::2]], 1)

2.第二步：models/yolo.py加上

 elif m is space_to_depth:
            c2 = 4 * ch[f]

同时在769行里面加入space to death

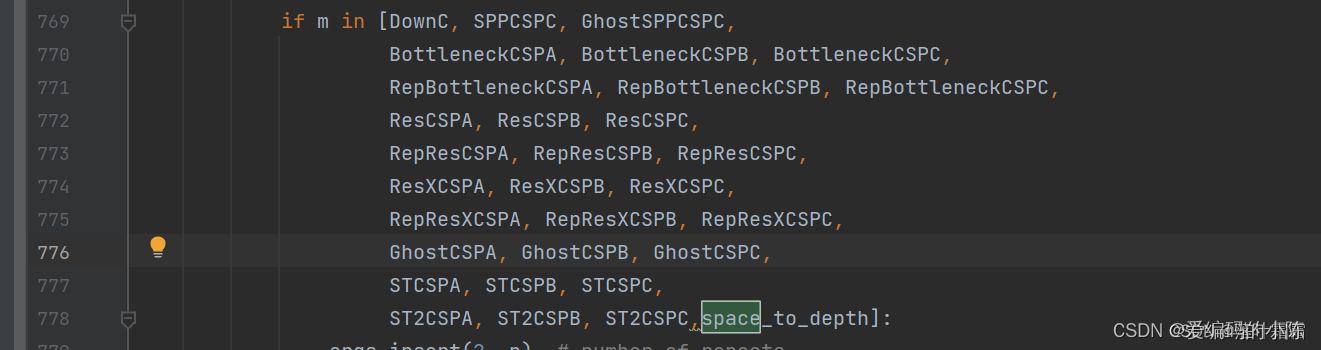
3.第三步：修改yolov7的yaml文件

# parameters
nc: 80  # number of classes
depth_multiple: 1.0  # model depth multiple
width_multiple: 1.0  # layer channel multiple

# anchors
anchors:
  - [12,16, 19,36, 40,28]  # P3/8
  - [36,75, 76,55, 72,146]  # P4/16
  - [142,110, 192,243, 459,401]  # P5/32

# yolov7 backbone
backbone:
  # [from, number, module, args]
  [[-1, 1, Conv, [32, 3, 1]],  # 0

   [-1, 1, Conv, [64, 3, 2]],  # 1-P1/2
   [-1, 1, Conv, [64, 3, 1]],

   [-1, 1, Conv, [128, 3, 2]],  # 3-P2/4
   [-1, 1, Conv, [64, 1, 1]],
   [-2, 1, Conv, [64, 1, 1]],
   [-1, 1, Conv, [64, 3, 1]],
   [-1, 1, Conv, [64, 3, 1]],
   [-1, 1, Conv, [64, 3, 1]],
   [-1, 1, Conv, [64, 3, 1]],
   [[-1, -3, -5, -6], 1, Concat, [1]],
   [-1, 1, Conv, [256, 1, 1]],  # 11

   [-1, 1, MP, []],
   [-1, 1, Conv, [128, 1, 1]],
   [-3, 1, Conv, [128, 1, 1]],
   [-1, 1, Conv, [128, 3, 2]],
   [[-1, -3], 1, Concat, [1]],  # 16-P3/8
   [-1, 1, Conv, [128, 1, 1]],
   [-2, 1, Conv, [128, 1, 1]],
   [-1, 1, Conv, [128, 3, 1]],
   [-1, 1, Conv, [128, 3, 1]],
   [-1, 1, Conv, [128, 3, 1]],
   [-1, 1, Conv, [128, 3, 1]],
   [[-1, -3, -5, -6], 1, Concat, [1]],
   [-1, 1, Conv, [512, 1, 1]],  # 24

   [-1, 1, MP, []],
   [-1, 1, Conv, [256, 1, 1]],
   [-3, 1, Conv, [256, 1, 1]],
   [-1, 1, Conv, [256, 3, 2]],
   [[-1, -3], 1, Concat, [1]],  # 29-P4/16
   [-1, 1, Conv, [256, 1, 1]],
   [-2, 1, Conv, [256, 1, 1]],
   [-1, 1, Conv, [256, 3, 1]],
   [-1, 1, Conv, [256, 3, 1]],
   [-1, 1, Conv, [256, 3, 1]],
   [-1, 1, Conv, [256, 3, 1]],
   [[-1, -3, -5, -6], 1, Concat, [1]],
   [-1, 1, Conv, [1024, 1, 1]],  # 37

   [-1, 1, MP, []],
   [-1, 1, Conv, [512, 1, 1]],
   [-3, 1, Conv, [512, 1, 1]],
   [-1, 1, Conv, [512, 3, 2]],
   [[-1, -3], 1, Concat, [1]],  # 42-P5/32
   [-1, 1, Conv, [256, 1, 1]],
   [-2, 1, Conv, [256, 1, 1]],
   [-1, 1, Conv, [256, 3, 1]],
   [-1, 1, Conv, [256, 3, 1]],
   [-1, 1, Conv, [256, 3, 1]],
   [-1, 1, Conv, [256, 3, 1]],
   [[-1, -3, -5, -6], 1, Concat, [1]],
   [-1, 1, Conv, [1024, 1, 1]],  # 50
  ]

# yolov7 head
head:
  [[-1, 1, SPPCSPC, [512]], # 51

   [-1, 1, Conv, [256, 1, 1]],
   [-1, 1, nn.Upsample, [None, 2, 'nearest']],
   [37, 1, Conv, [256, 1, 1]], # route backbone P4
   [[-1, -2], 1, Concat, [1]],

   [-1, 1, Conv, [256, 1, 1]],
   [-2, 1, Conv, [256, 1, 1]],
   [-1, 1, Conv, [128, 3, 1]],
   [-1, 1, Conv, [128, 3, 1]],
   [-1, 1, Conv, [128, 3, 1]],
   [-1, 1, Conv, [128, 3, 1]],
   [[-1, -2, -3, -4, -5, -6], 1, Concat, [1]],
   [-1, 1, Conv, [256, 1, 1]], # 63

   [-1, 1, Conv, [128, 1, 1]],
   [-1, 1, nn.Upsample, [None, 2, 'nearest']],
   [24, 1, Conv, [128, 1, 1]], # route backbone P3
   [[-1, -2], 1, Concat, [1]],

   [-1, 1, Conv, [128, 1, 1]],
   [-2, 1, Conv, [128, 1, 1]],
   [-1, 1, Conv, [64, 3, 1]],
   [-1, 1, Conv, [64, 3, 1]],
   [-1, 1, Conv, [64, 3, 1]],
   [-1, 1, Conv, [64, 3, 1]],
   [[-1, -2, -3, -4, -5, -6], 1, Concat, [1]],
   [-1, 1, Conv, [128, 1, 1]], # 75

   [-1, 1, MP, []],
   [-1, 1, Conv, [128, 1, 1]],
   [-3, 1, Conv, [128, 1, 1]],
   [-1, 1, Conv, [128, 3, 2]],
   [[-1, -3, 63], 1, Concat, [1]],

   [-1, 1, Conv, [256, 1, 1]],
   [-2, 1, Conv, [256, 1, 1]],
   [-1, 1, Conv, [128, 3, 1]],
   [-1, 1, Conv, [128, 3, 1]],
   [-1, 1, Conv, [128, 3, 1]],
   [-1, 1, Conv, [128, 3, 1]],
   [[-1, -2, -3, -4, -5, -6], 1, Concat, [1]],
   [-1, 1, Conv, [256, 1, 1]], # 88

   [-1, 1, MP, []],
   [-1, 1, Conv, [256, 1, 1]],
   [-3, 1, Conv, [256, 1, 1]],
   [-1, 1, Conv, [256, 3, 2]],
   [[-1, -3, 51], 1, Concat, [1]],

   [-1, 1, Conv, [512, 1, 1]],
   [-2, 1, Conv, [512, 1, 1]],
   [-1, 1, Conv, [256, 3, 1]],
   [-1, 1, Conv, [256, 3, 1]],
   [-1, 1, Conv, [256, 3, 1]],
   [-1, 1, Conv, [256, 3, 1]],
   [[-1, -2, -3, -4, -5, -6], 1, Concat, [1]],
   [-1, 1, Conv, [512, 1, 1]], # 101
   [-1,1,space_to_depth,[1]],   # 2 -P2/4
   [-1, 1, Conv, [512, 1, 1]], # 103

   [75, 1, RepConv, [256, 3, 1]],
   [88, 1, RepConv, [512, 3, 1]],
   [103, 1, RepConv, [1024, 3, 1]],

   [[104,105,106], 1, IDetect, [nc, anchors]],   # Detect(P3, P4, P5)
  ]