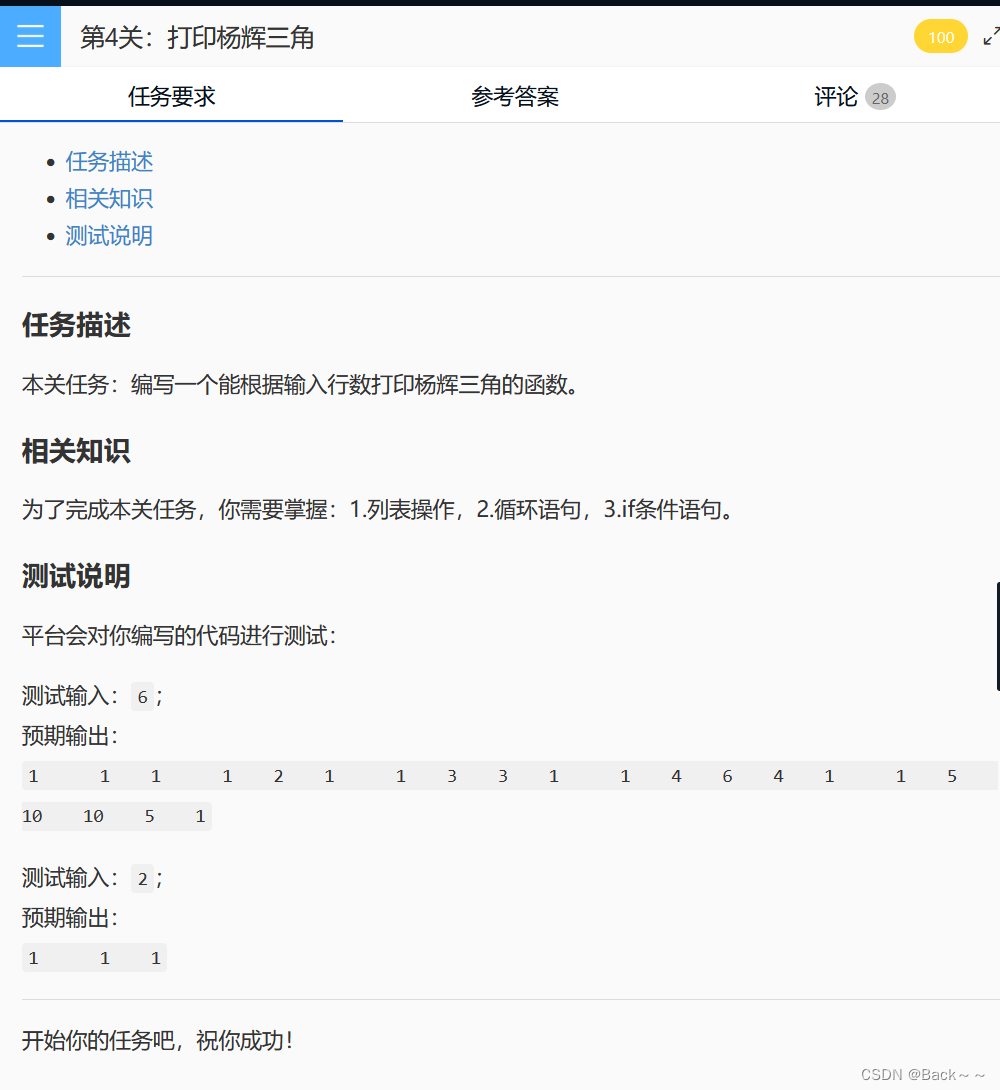
小红的子序列权值和 (nowcoder.com)



#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e5+6;
const int inf=0x3f3f3f3f;
const double pi=acos(-1.0);
const int mod=1e9+7;
int c[1100][1100];
int a[1100],b[5];
void solve()
{
int n;
cin>>n;
//计算组合数:
for(int i=0;i<=n;i++)
{
for(int j=0;j<=i;j++)
{
if(j==0||j==i)c[i][j]=1;
else c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
}
}
//统计每个数出现次数:
for(int i=0;i<n;i++)
{
cin>>a[i];
b[a[i]]++;
}
//计算2的(1出现次数)次方:
int cn=1;
for(int i=0;i<b[1];i++)cn=cn*2%mod;
//分别求([乘积为多少时]的价值:是(i+1)*(j+1))*([乘积为多少时]的个数)
int ans=0;
for(int i=0;i<=b[2];i++)
{
for(int j=0;j<=b[3];j++)
{
ans=ans+c[b[2]][i]%mod*c[b[3]][j]%mod*(i+1)*(j+1)%mod*cn%mod;
ans%=mod;
}
}
cout<<(ans-1+mod)%mod;
}
signed main()
{
ios_base::sync_with_stdio(false);
cin.tie(nullptr),cout.tie(nullptr);
int t=1;
//cin>>t;
while(t--)
{
solve();
}
return 0;
}
//优化后:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5 + 6;
const int inf = 0x3f3f3f3f;
const int mod=1e9+7;
int h[5]={};
//快速幂:
int power(int a,int b)
{
int result=1;
while(b)
{
if(b&1)
{
b/=2;
result=result*a%mod;
a=a*a%mod;
}
else
{
a=a*a%mod;
b/=2;
}
}
return result;
}
//求逆元:
int ni(int x)
{
return power(x,mod-2);
}
int jc[101010];
//求组合数:C(n,m)=n!/(m!*(n-m)!)
int C(int n,int m)
{
return jc[n]%mod*ni(jc[m])%mod*ni(jc[n-m])%mod;
}
void solve()
{
int n;
cin>>n;
jc[0]=1;
//cout<<power(2,2)<<endl;
for(int i=1;i<=n;i++)jc[i]=(jc[i-1]*i)%mod;
int x;
for(int i=0;i<n;i++)
{
cin>>x;
h[x]++;
}
int cn=1,c2=0,c3=0;
for(int i=0;i<h[1];i++)cn=cn*2%mod;
//分别求c(h[2],i)*(i+1)和c(h[3],j)*(j+1)
for(int i=0;i<=h[2];i++)
{
c2+=C(h[2],i)*(i+1)%mod;
c2%=mod;
}
for(int i=0;i<=h[3];i++)
{
c3+=C(h[3],i)*(i+1)%mod;
c3%=mod;
}
cout<<(c2*c3%mod*cn%mod-1+mod)%mod;
}
signed main()
{
ios_base::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
int t = 1;
//cin>>t;
while (t--) {
solve();
}
return 0;
}
![[DevOps云实践] 跨AWS账户及Region调用Lambda](https://img-blog.csdnimg.cn/direct/62490489902546c9acdd4b95fa6a4836.png)