📢编程环境：idea
📢树结构，以及叶子，结点，度等一些名词是什么意思，本篇不再赘述。

1. 认识二叉树

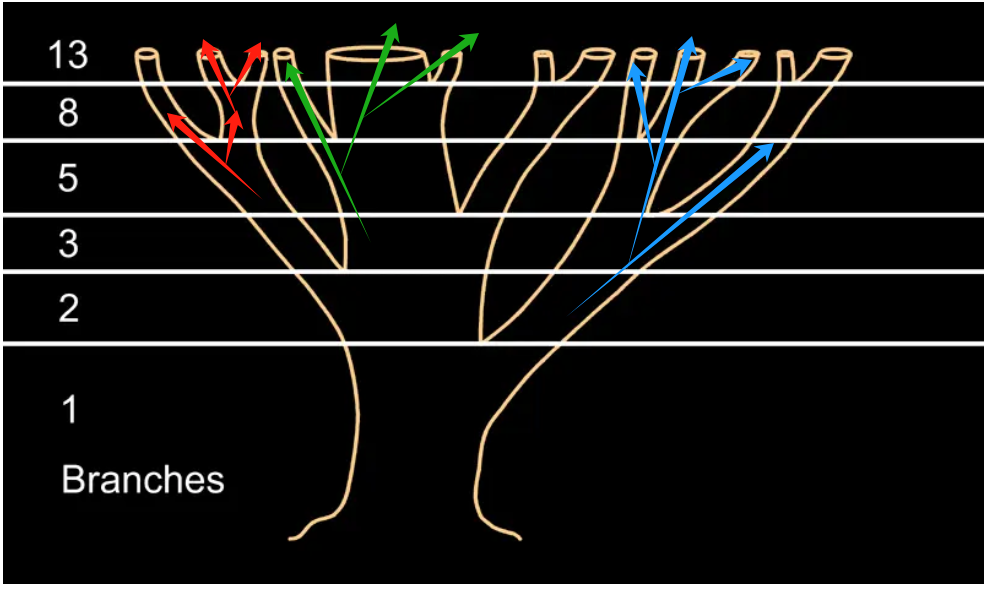
二叉树是重要的数据结构之一，之所以叫二叉树，是因为用它组织的数据逻辑上就像一颗自然界中倒挂的二叉树一样。即树的根朝上，所有树枝只要遇到分叉，当下最多分两个叉，树枝朝下。

1.1 二叉树的结构

先来理解二叉树的逻辑结构：

二叉树是一种逻辑上非线性的数据结构。一颗二叉树是一个有限个元素的集合。该集合或者为空，或者由一个根元素加上两颗别称为左子树和右子树的二叉树组成。这也是二叉树的递归性，一颗二叉树是由一个套一个的子二叉树构成的。还要注意的是，左右子树的次序不能颠倒。

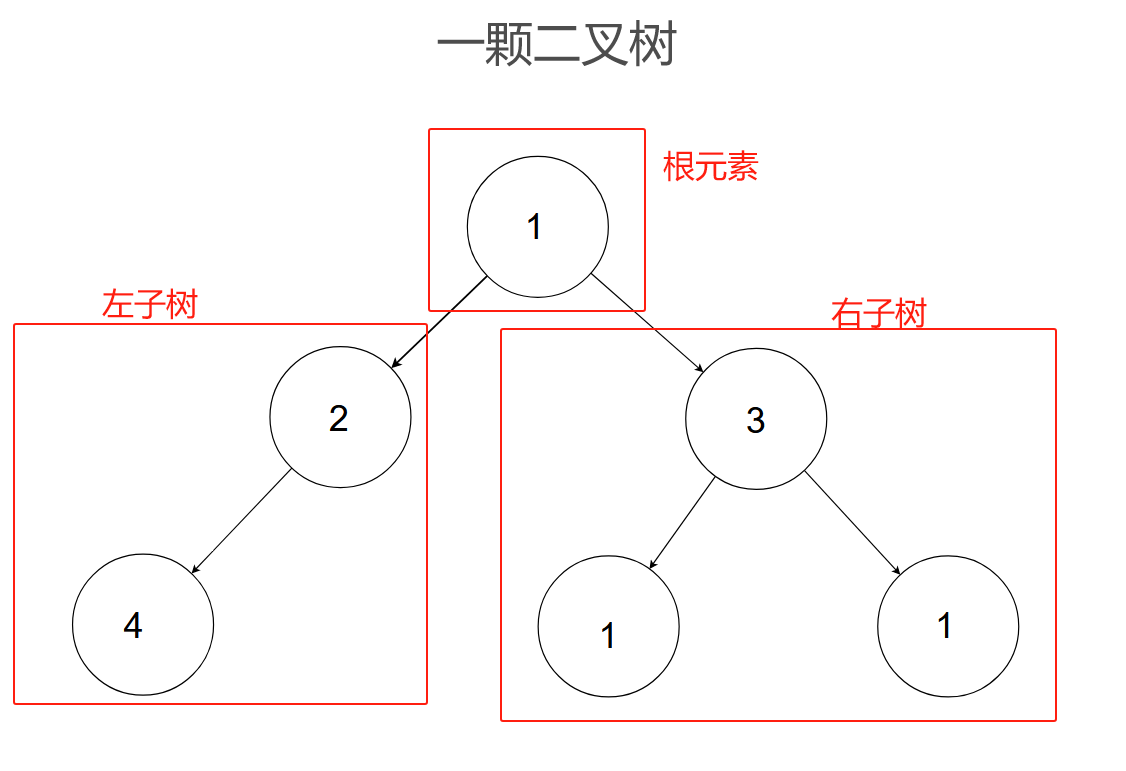
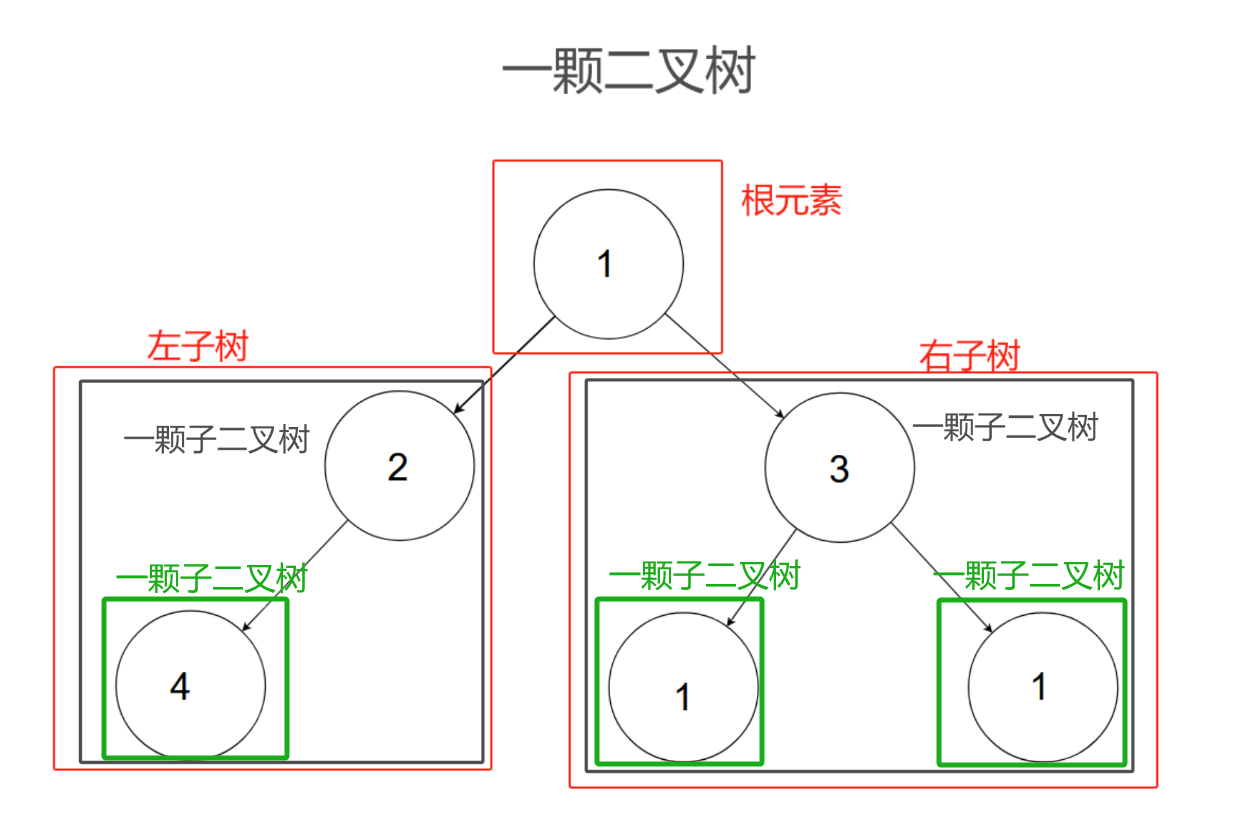
对于二叉树中的每个元素，它都有唯一一个前驱(除头元素没有前驱)和不超过两个后继（不超过两个后继的意思是：后继的个数可以是0,1,2）

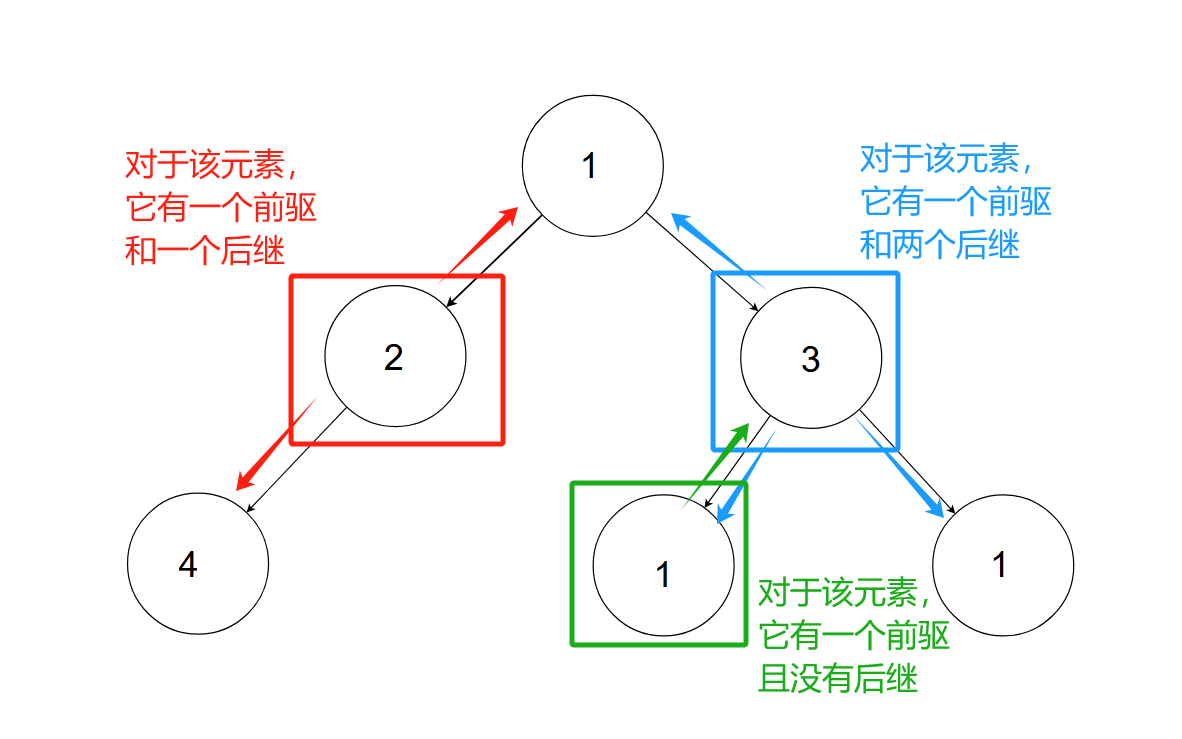
即对于任意的二叉树都是由以下几种情况复合而成的：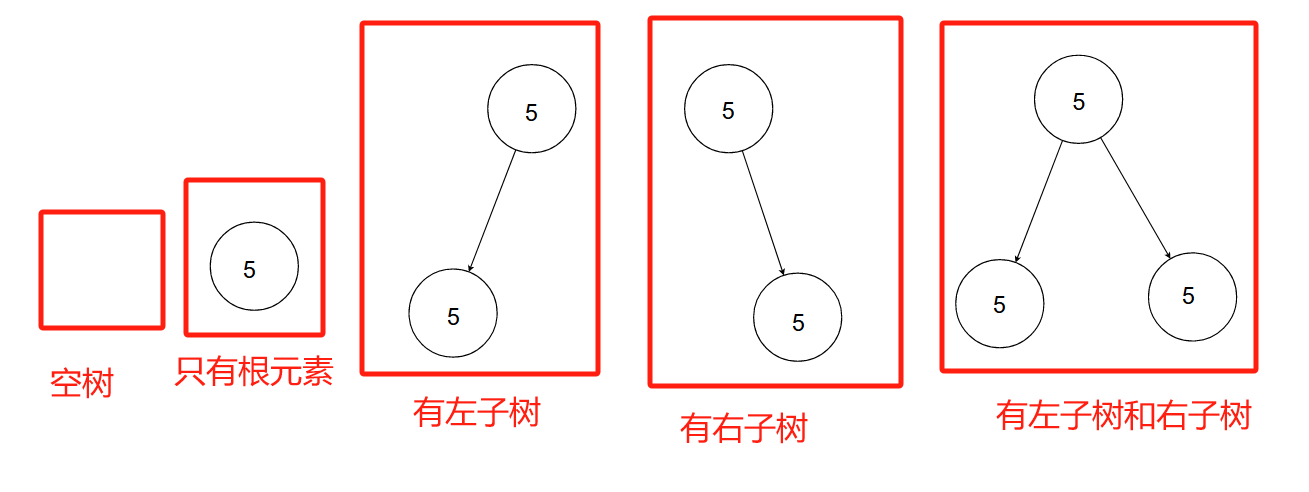

---

再来理解二叉树的(物理)存储结构：

二叉树的存储结构分为顺序存储和类似于链表的链式存储。本篇以实现二叉树的链式存储结构为主。

先来回忆一下链表的链式存储：用链表存储一组元素，其中每个元素都存储在一个结点中。单链表的每个结点中存储元素的同时，还要存储下一个元素的地址，双向链表的每个结点中存储元素的同时，还要存储上一个元素的结点地址和下一个元素的结点地址。

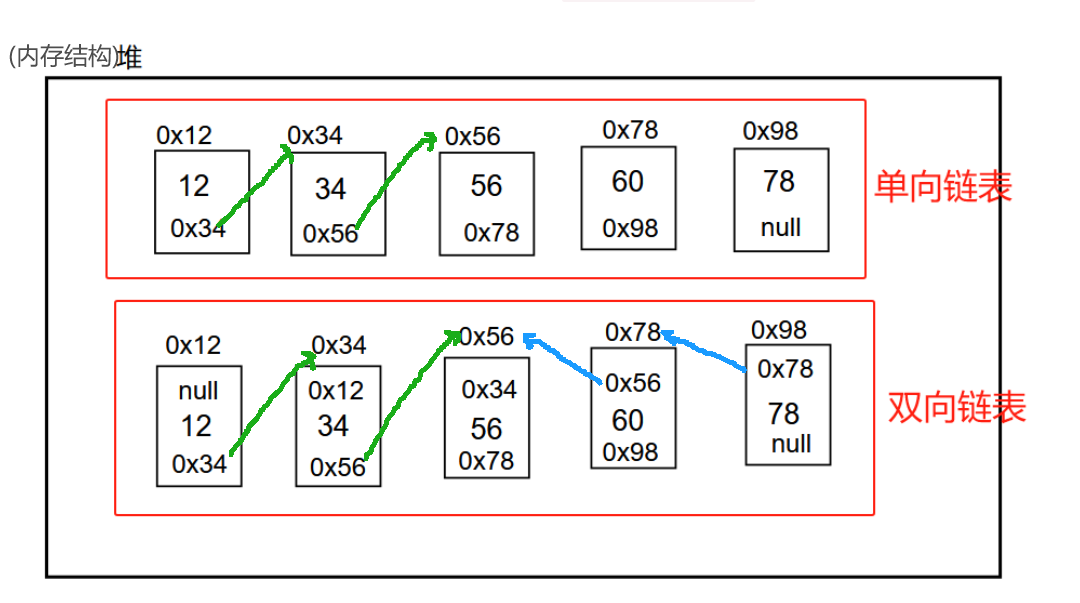
而二叉树的链式存储，也是把每个元素都存储在一个结点中，但是不同于链表为了保持逻辑上的线性结构，结点中存元素的同时还要存储前一个和后一个元素的节点地址。而二叉树在逻辑上是非线性的树结构，为了保持该结构，二叉树的每个节点中存储元素的同时，还要存储它的前驱结点地址和后继结点地址。

二叉树的每个结点中如果同时存元素，前驱结点地址，后继结点地址，统一又把这种链式存储方式叫做孩子表示法。例如用孩子表示法存储下面这颗二叉树：

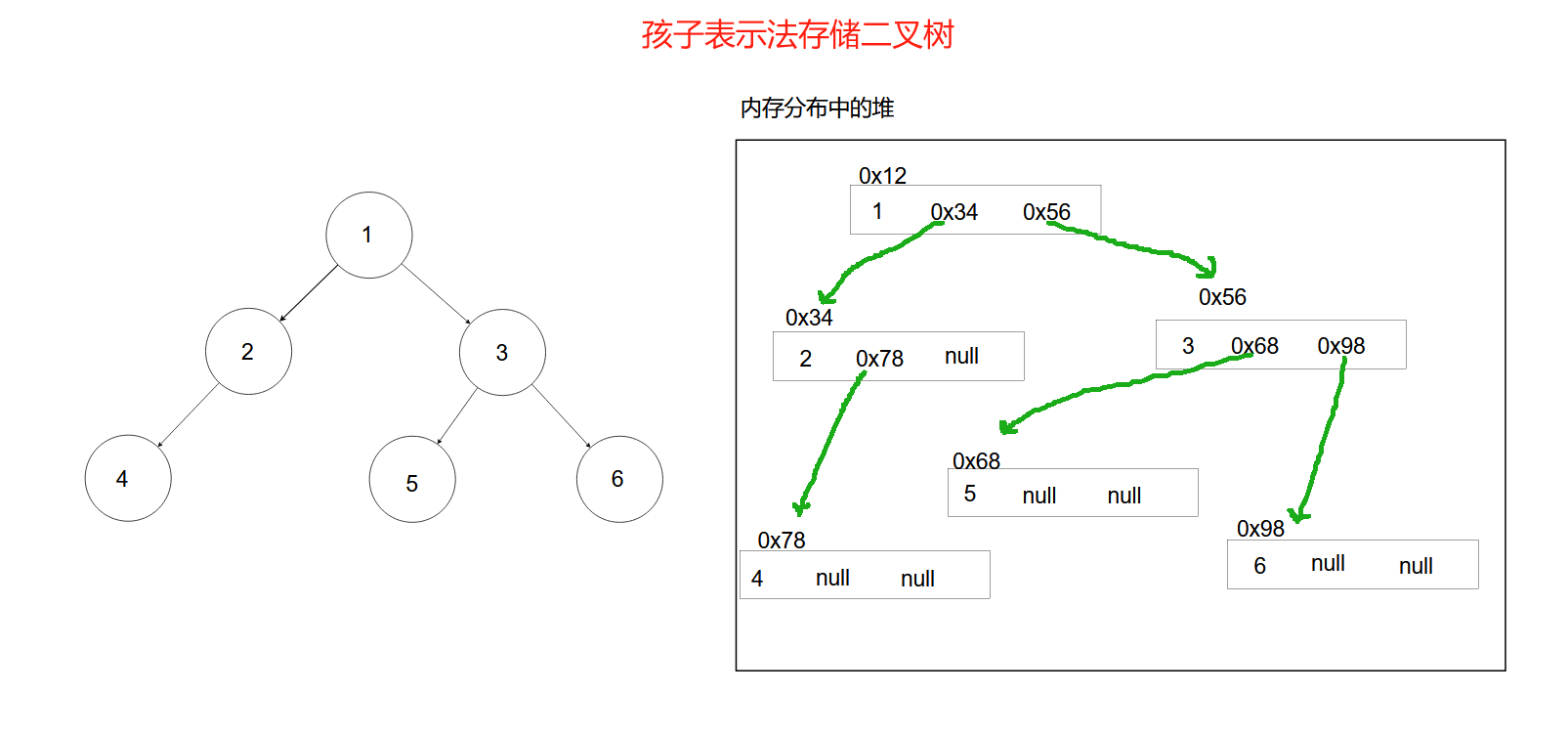
二叉树的每个结点中如果存元素，和后继结点地址，统一又把这种链式存储方式叫做孩子双亲表示法。
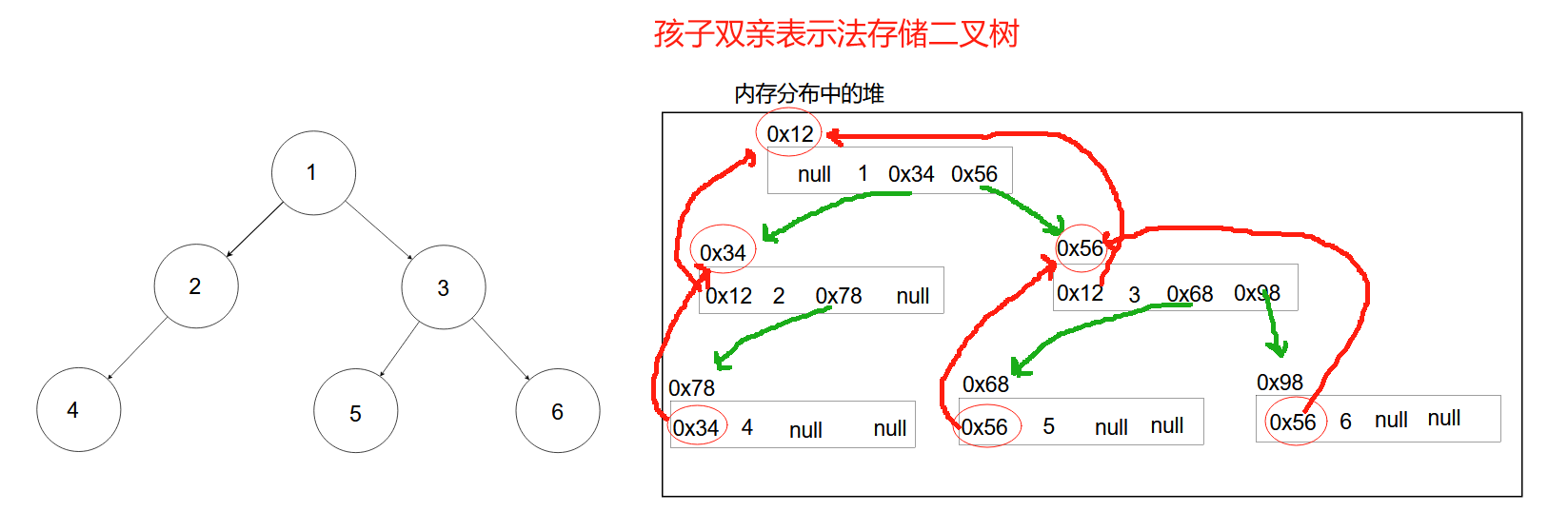其中，自上而下看一颗二叉树，根元素所在的结点又叫做根结点。

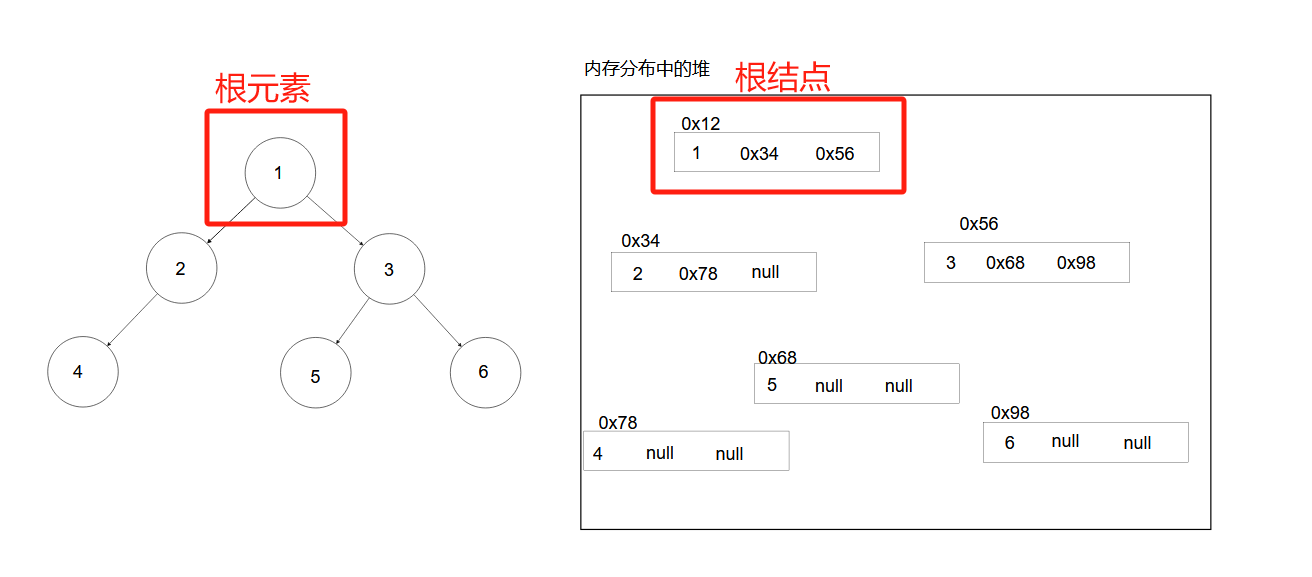
本篇要用java语言模拟实现孩子表示法存储二叉树，以及一些常用基本操作，孩子双亲表示法存储二叉树会在后续总结AVL树，红黑树的博客中重点介绍，二叉树的顺序存储会在后续总结 堆 的博客中重点介绍。

1.2 两种特殊的二叉树

1.21 满二叉树

一颗二叉树，如果每层的结点数都达到最大值，即每个元素都有两个后继，则这颗二叉树就是满二叉树。

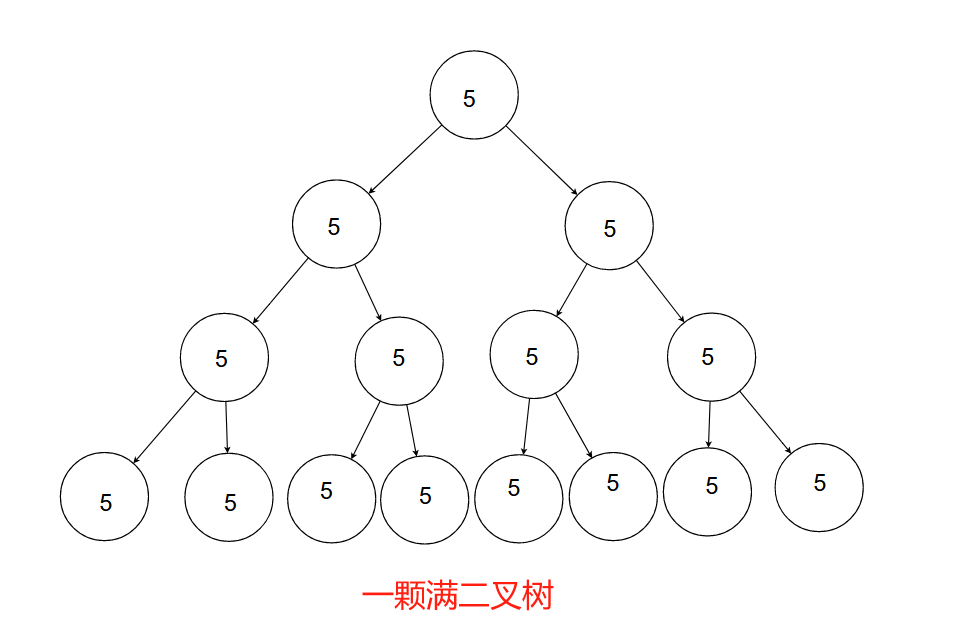
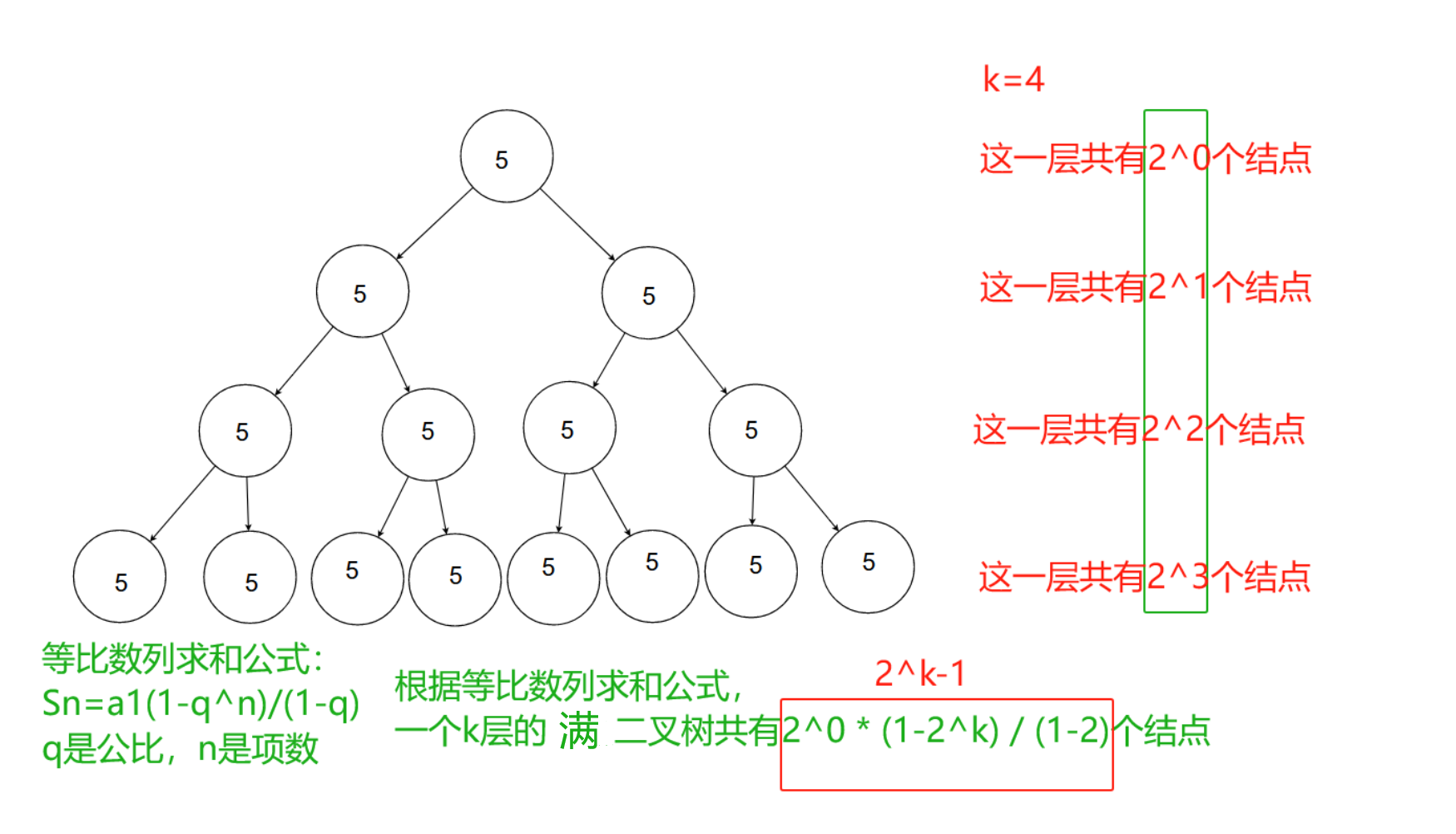
其中，假设满二叉树的层数是k，则该满二叉树的节点总数是(2^k)-1即2的k次方-1。

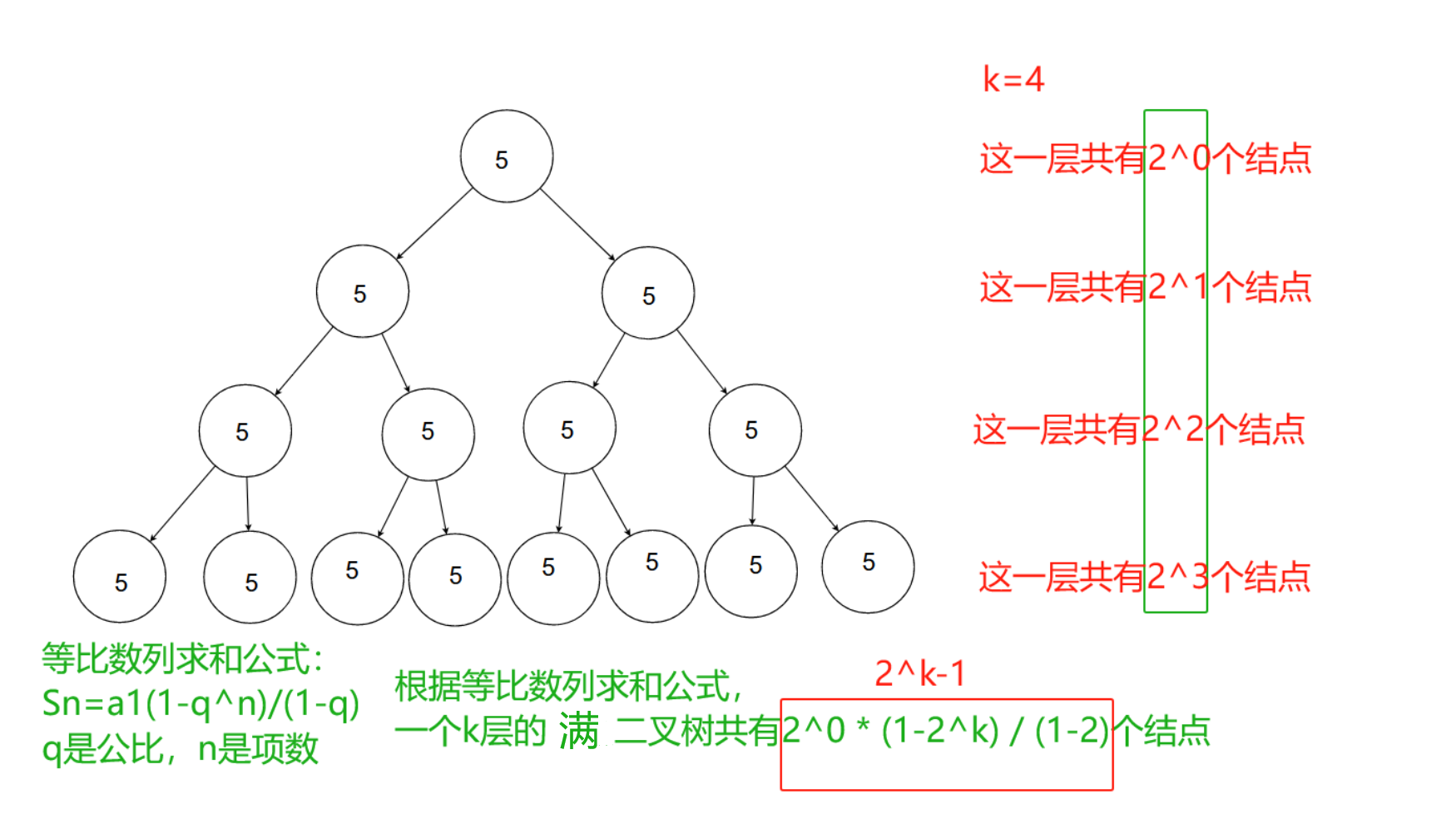
1.22 完全二叉树

完全二叉树是由满二叉树引出来的。

对于深度为k的，有n个结点的二叉树，当且仅当它的每个结点都与深度为k的满二叉树中编号从0至n-1的节点一一对应时，该二叉树才能称之为完全二叉树。（其中满二叉树中结点按从左到右，从上到下的顺序进行编号，此处假设根节点从0号开始）。

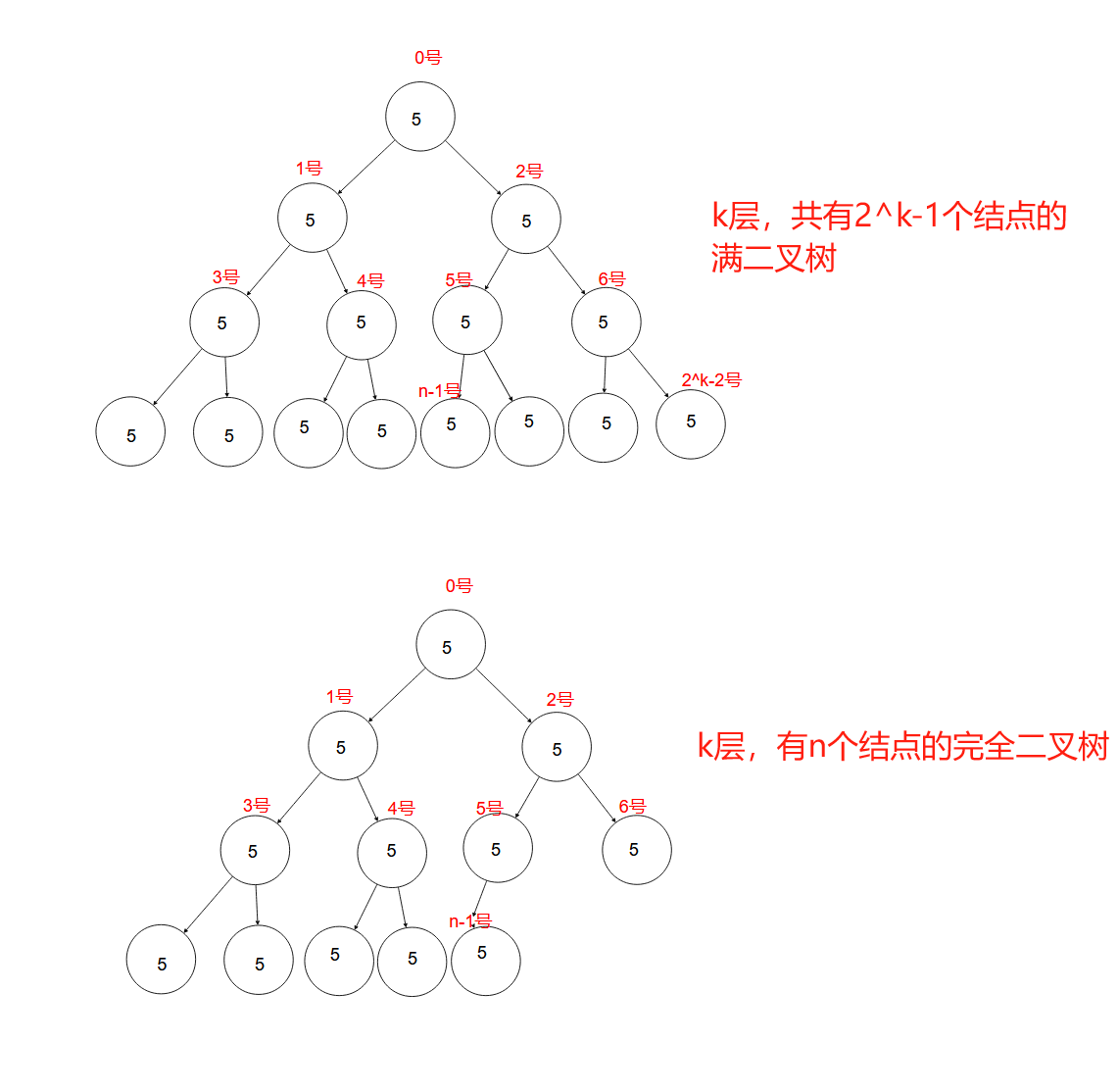
满二叉树是特殊的完全二叉树。

1.3 二叉树的性质

1. 若规定只有根节点的二叉树深度为1，则深度为k的二叉树最多有2^k-1个结点（满二叉树）。（k>=0）

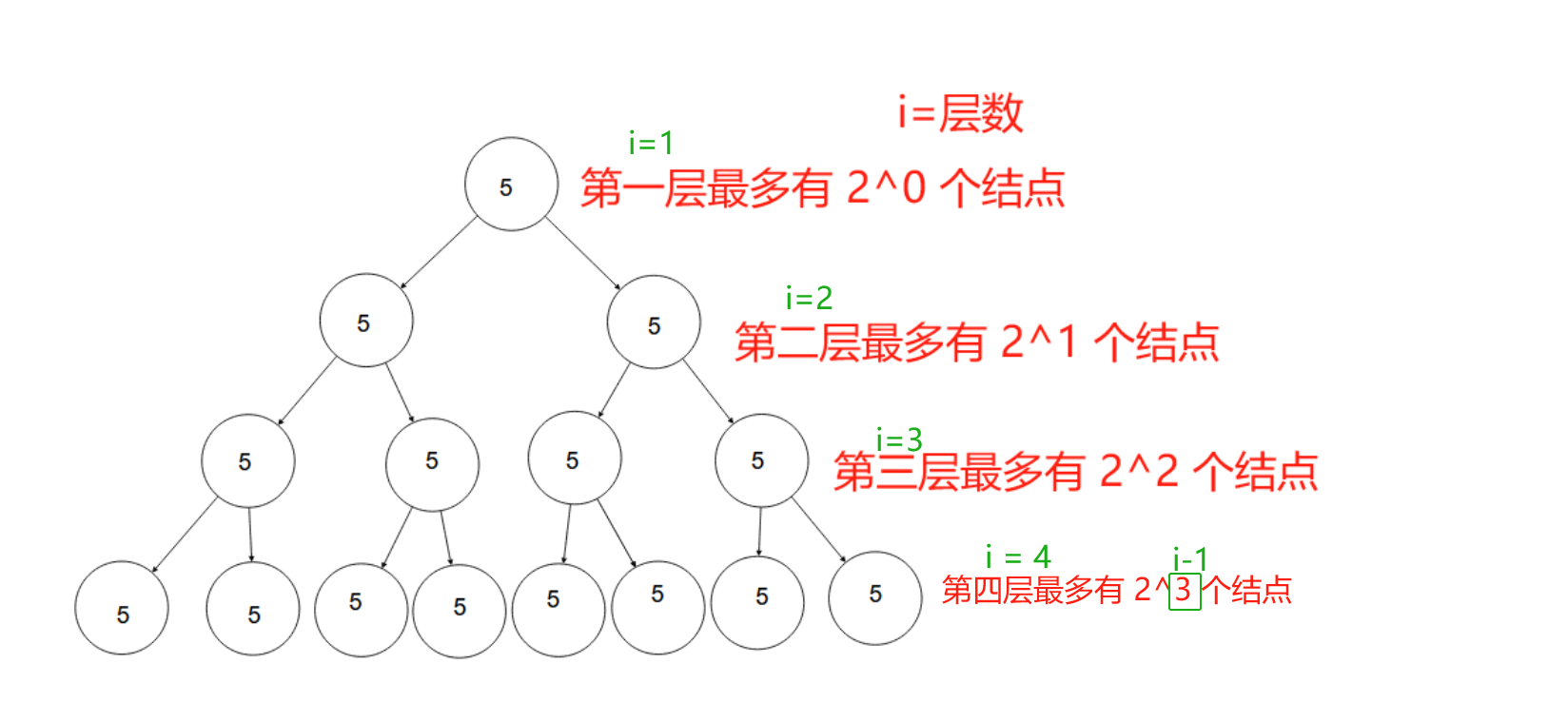
2. 若规定根节点是第一层，则一颗非空二叉树的第 i 层上最多有 2^(i-1) 个结点。(i>0)

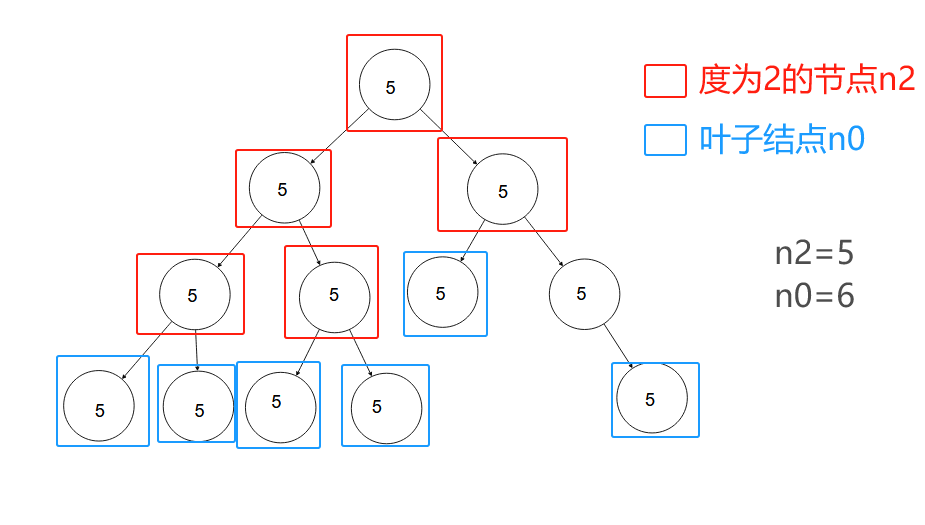
3. 对任何一颗二叉树，如果其叶结点个数为n0，度为2的结点个数为n2，则有n0=n2+1。

   • 其实就是，在任意一颗二叉树中，叶子结点个数永远比度为2的结点个数多一个。
     

     • 在二叉树中，若一个结点没有后继，则该结点就是叶子结点。
     • 度就是一个结点有几个后继，若一个结点有一个后继，该结点度为1；若一个结点有两个后继，该结点度为2。

   • 推论：

     • 在任意一颗二叉树当中，假设，该二叉树的叶子结点个数为n0，度为1的结点个数为n1，度为2的结点个数为n2，设这颗二叉树的总结点个数为N。所以：N=n0+n1+n2。
     • 又因为：一颗有N个结点的树有N-1条边。叶子结点向下不会产生边；度为1的结点向下会产生一条边，即n1个结点产生边的个数是n1。度为2的结点向下会产生两条边，即n2个结点产生边的个数是2*n2。所以：N-1=n1+2 * n2，即N=n1+2*n2 +1。
     • 两个式子联立最后推出：n0=n2+1。

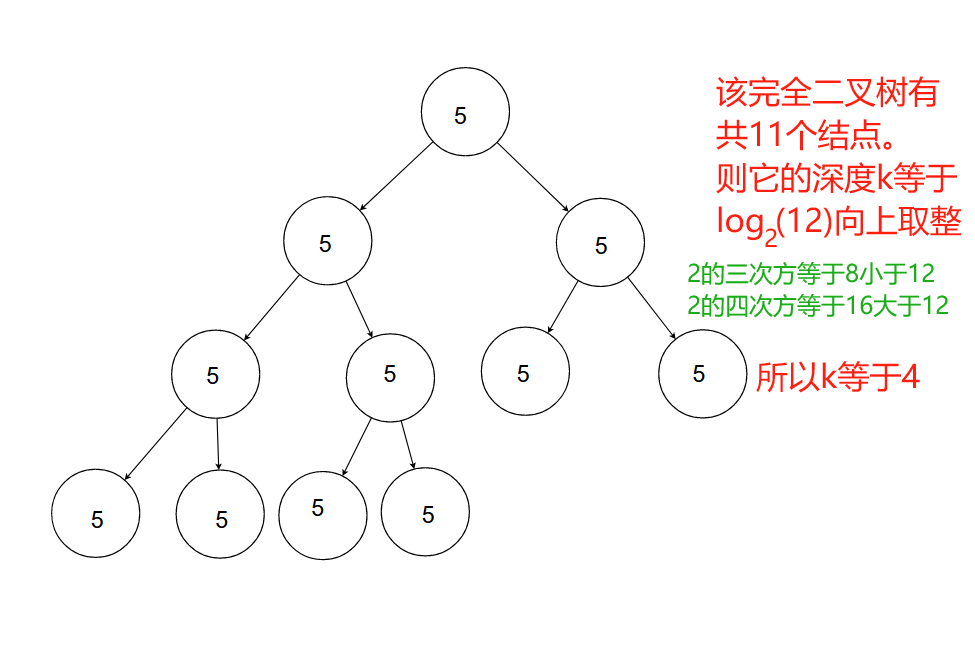
4. 具有n个结点的完全二叉树，其深度k为log₂(n+1) 向上取整。

5. 对于有n个结点的完全二叉树，假设按照从左到右，从上到下的顺序对所有结点从0开始编号，根节点为0号，最后一个结点时 n-1 号。
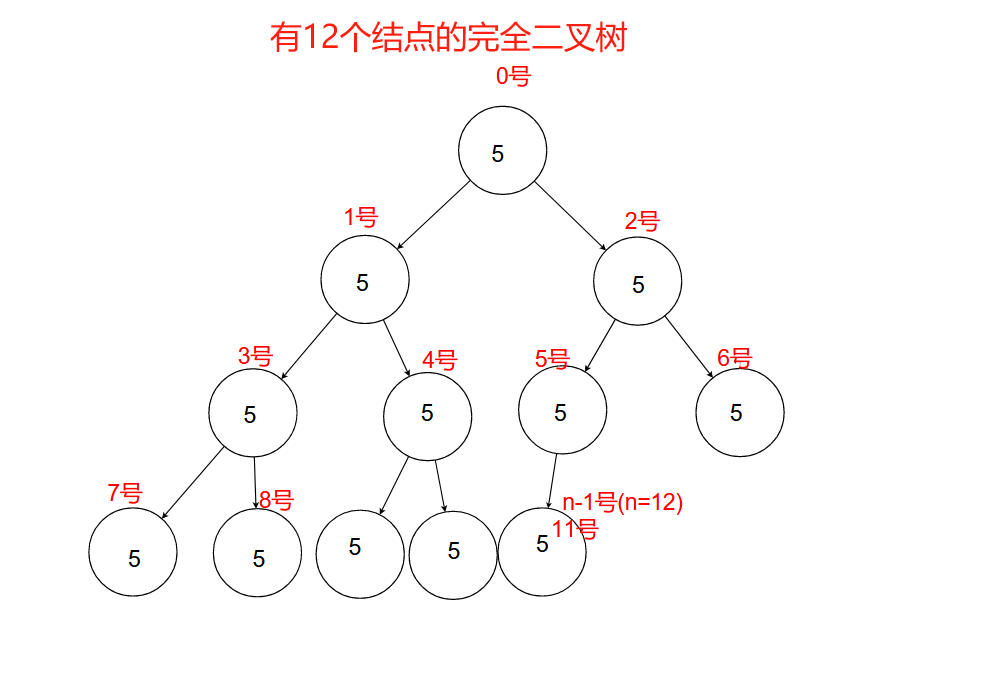
   • 已知 一个结点是 i 号，则它的双亲节点（前驱结点）的编号是 (i-1)/2 。根结点是0号，没有双亲结点。
   • 已知 一个结点是 i 号，则它的左孩子结点的编号是 2i+1(2i+1<n)。若2i+1>n，该左孩子不存在，即 i 号结点没有左孩子。
   • 已知 一个结点是 i 号，则它的右孩子结点的编号是 2i+2(2i+2<n)。若2i+2>n，该右孩子不存在，即 i 号结点没有右孩子。

---

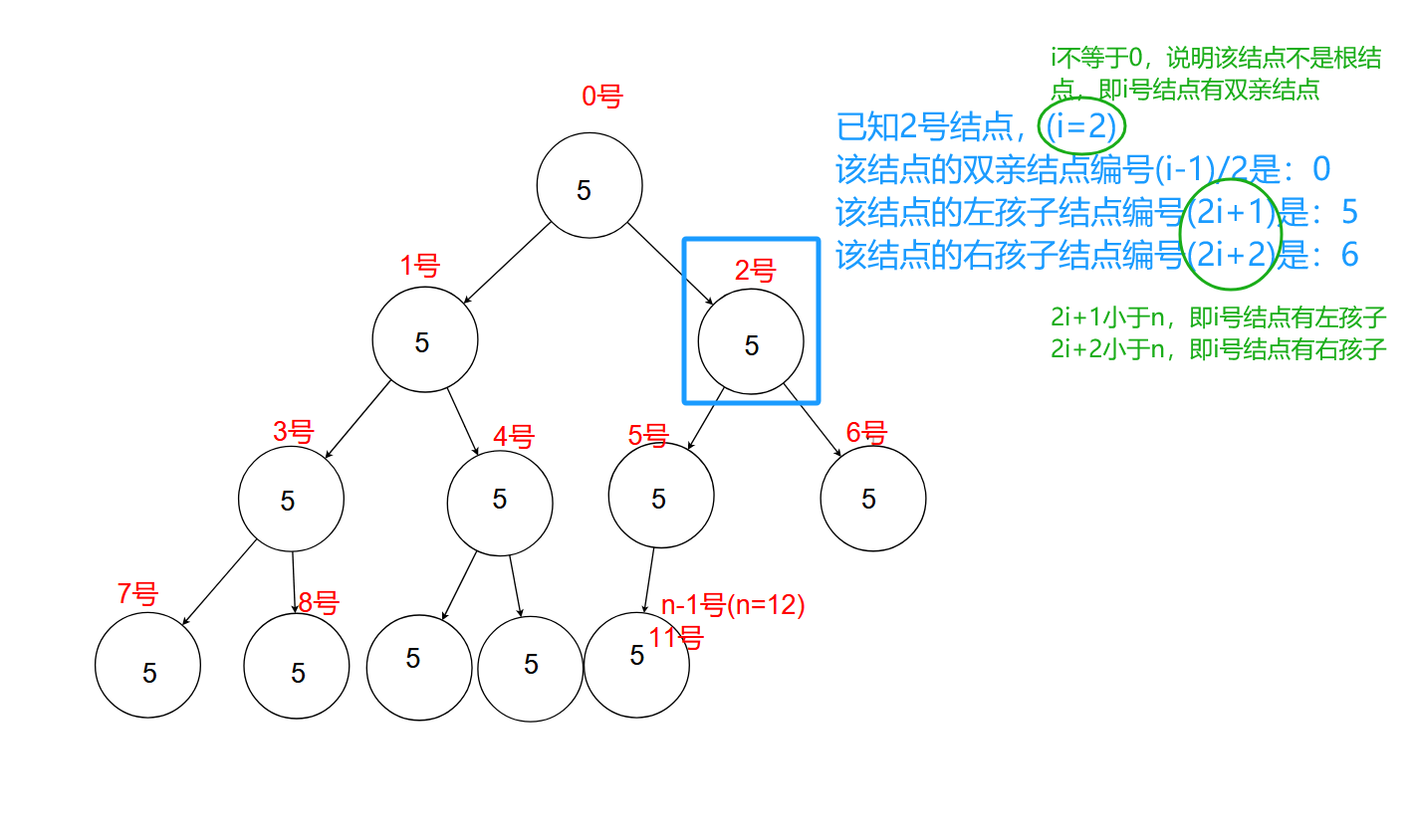
二叉树的结构和性质我们都要非常熟悉，才能在此基础上更好的解决有关二叉树的相关题目，以及在实际场景中应用二叉树。

2. java语言，模拟实现二叉树的链式结构之孩子表示法（以存char类型元素为例）

用java语言模拟实现一个二叉树，java是面向对象语言，所以首先要创建一个类来表示二叉树，这个类里面有一个静态内部类，一个成员变量，若干个成员方法。静态内部类是为了描述结点，结点中要存储元素，左孩子地址，右孩子地址（孩子表示法）；成员变量是二叉树的根结点；通过成员方法对二叉树进行遍历，以及增删改查操作。

public class MyBinaryTree {
    public static class Node{
        int val;//元素域
        Node left;//左孩子的引用，常常代表左孩子为根的整颗左子树
        Node right;//右孩子的引用，常常代表右孩子为根的整颗右子树
        Node(int val){
            this.val = val;
        }
        private Node root;//二叉树的根节点
        
        //仅博客需要，先穷举法创建一个二叉树，方便演示二叉树的遍历，实际场景中不要用这种方法创建二叉树
        public void createMyBinaryTree(){

        }
        //前序遍历
        void preOrder(Node root){
            ;
        }
        //中序遍历
        void inOrder(Node root){
            ;
        }
        //后序遍历
        void postOrder(Node root){
            ;
        }
        //二叉树的构建(结点中存char类型的元素)
        Node create(String str){
            return null;
        }

        // 获取树中节点的个数
        int size(Node root){
            return -1;
        }

        // 获取叶子节点的个数
        int getLeafNodeCount(Node root){
            return -1;
        }

        // 子问题思路-求叶子结点个数
        int getLeafNodeCount1(Node root){
            return -1;
        }

        // 获取第K层节点的个数
        int getKLevelNodeCount(Node root,int k){
            return -1;
        }

        // 获取二叉树的高度
        int getHeight(Node root){
            return -1;
        }

        // 检测值为value的元素是否存在
        Node find(Node root, int val){
            return null;
        }

        //层序遍历
        void levelOrder(Node root){

        }

        // 判断一棵树是不是完全二叉树
        boolean isCompleteTree(Node root){
            return true;
        }
    }
}

2.1 二叉树的遍历

2.11 前序遍历

2.12 中序遍历

2.13 后序遍历

2.2 创建一颗二叉树