7. 决策树

7.1 ID算法

核心是在决策树各个节点上应用信息增益准则选择特征，递归的构建决策树。

具体方法是：从根结点开始，对结点计算所有可能的特征的信息增益，选择信息增益最大的特征作为结点的特征，由该特征的不同取值建立子结点；再对子结点递归的调用以上方法，构建决策树；直到所有特征的信息增益均很小或没有特征可以选择为止。ID3相当于用极大似然法进行概率模型的选择。使用二元切分法则易于对树构建过程中进行调整以处理连续型特征。

具体的处理方法是: 如果特征值大于给定值就走左子树，否则走右子树。另外二元切分法也节省了树的构建时间。

7.2 C4.5算法

        算法用信息增益率选择特征，在树的构造过程中会进行剪枝操作优化，能够自动完成对连续属性的离散化处理；在选择分割属性时选择信息增益率最大的属性。

7.2.1 C4.5为什么使用信息增益率

        在使用信息增益的时候，如果某个特征有很多取值，使用这个取值多的特征会的大的信息增益，这个问题是出现很多分支，将数据划分更细，模型复杂度高，出现过拟合的机率更大。使用信息增益比就是为了解决偏向于选择取值较多的特征的问题. 使用信息增益比对取值多的特征加上的惩罚，对这个问题进行了校正.

7.3 CART算法

分类与回归树 —— 使用二元切分法来处理连续型数值。

使用Gini作为分割属性选择的标准，择Gini最大的作为当前数据集的分割属性。

Gini：表示在样本集合中一个随机选中的样本被分错的概率。

Gini指数越小表示集合中被选中的样本被分错的概率越小，也就是说集合的纯度越高，反之，集合越不纯。

即 基尼指数（基尼不纯度）= 样本被选中的概率 * 样本被分错的概率

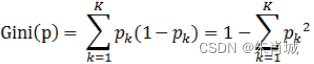
CART算法由以下两步组成：

决策树生成：基于训练数据集生成决策树，生成的决策树要尽量大；

决策树剪枝：用验证数据集对已生成的树进行剪枝并选择最优子树，这时用损失函数最小作为剪枝的标准。

7.3.1 基尼指数和信息熵都表示数据不确定性，为什么CART使用基尼指数？

        信息熵0, logK都是值越大，数据的不确定性越大. 信息熵需要计算对数，计算量大；信息熵是可以处理多个类别，基尼指数就是针对两个类计算的，由于CART树是一个二叉树，每次都是选择yes or no进行划分，从这个角度也是应该选择简单的基尼指数进行计算.