1. 在本节的估计问题中使用λ的值进行实验。绘制训练和测试精度关于λ的函数。观察到了什么？

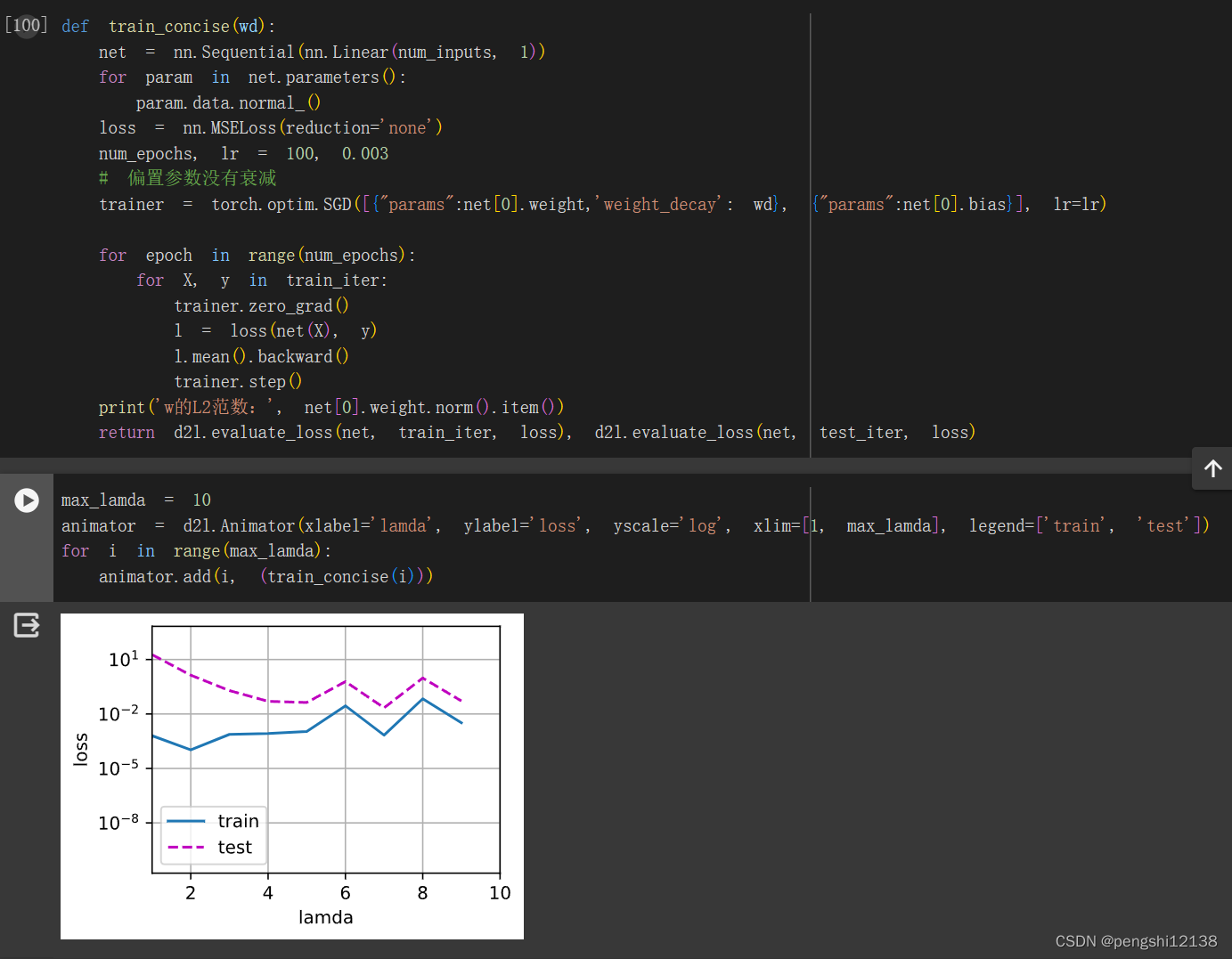
修改代码运行如图所示，可以发现对于lamda值的变化而言，对于训练loss和测试loss的影响不大。但是如果λ 太大后，train和test的loss会变得很大，太小后，train的loss会低，但是test的loss会很高。

2. 使用验证集来找到最佳值λ。它真的是最优值吗？这有关系吗？

不是，因为验证集上数据与其他数据集的数据可能不同，lamda只是对于验证数据集的最优值，而不是泛化情况下的最优值。关系上，只是划分数据降低超参数之间的影响，实现事件发生的独立而已，能够提高模型泛化能力。

3. 解答

$$\begin{array}{rl}L(w,b)& =\frac{1}{n}\sum _{i=1}^n\frac{1}{2}(w^T{x}^{(i)}+b-y^i{)}^2+\frac{\lambda }{2}|w|\\ \frac{\delta {\sum }_i^{}|w_i|}{\delta |w_i|}& =sgn(w_i)\\ w& \leftarrow w-\eta \lambda sgn(w_i)-\frac{\eta }{|\mathrm{B}|}\sum _{i\in \mathrm{B}}{x}^{(i)}(w^T{x}^{(i)}+b-y^{(i)})\end{array}$$

4. 解答

Frobenius 本质上就是 ||w||2

5. 解答

dropout层处理过拟合问题

6. 解答