全文摘要
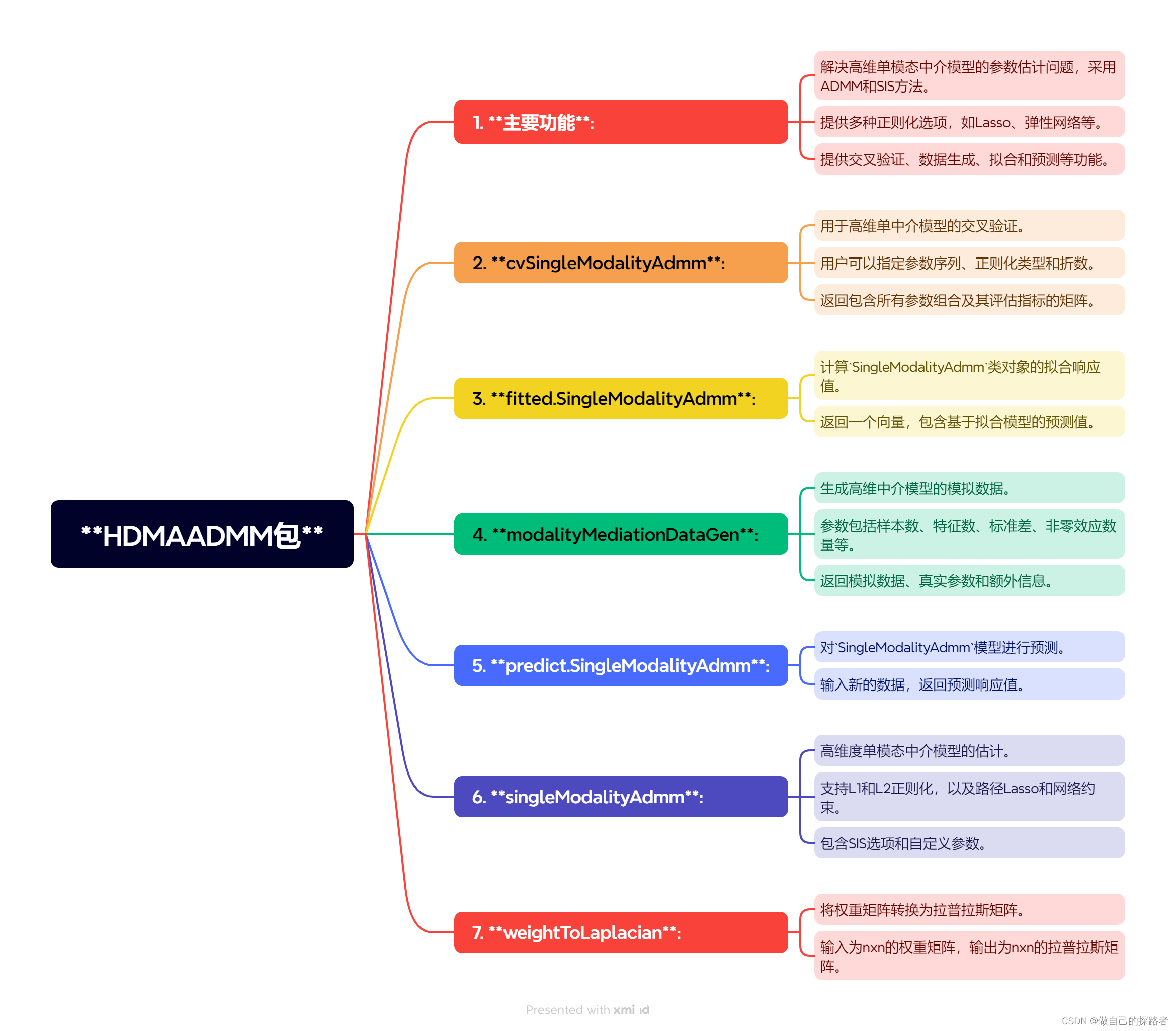
用于高维度单模态中介模型的参数估计,采用交替方向乘子法(ADMM)进行计算。该包提供了确切独立筛选(SIS)功能来提高中介效应的敏感性和特异性,并支持Lasso、弹性网络、路径Lasso和网络约束惩罚等不同正则化方法。
Pathway Lasso
背景
传统的结构方程建模(SEM)在处理大量中介变量时变得不稳定且计算复杂。Pathway Lasso引入了一个新的惩罚函数,它是一种非凸乘积函数的凸松弛,使得同时估计和选择路径效应成为可能。通过使用交替方向乘子法(ADMM)的算法,Pathway Lasso可以以闭合形式求解参数,并且其估计器在大样本下具有渐近一致性。Pathway Lasso的新方法用于在高维中介变量的情况下估计和选择路径效应。
实现方法
Pathway Lasso是一种针对高维中介变量问题的新方法,它通过结构方程建模(SEM)的正则化途径来处理。在高维设置中,当中介变量的数量接近或大于样本量时,该方法聚焦于估计和选择路径效应。为了改善估计的稳定性,Pathway Lasso避免将高维中介变量直接降低为线性组合,这通常是通过主成分分析(PCA)或其他矩阵分解技术实现的,但这些方法限制了对每个中介路径的解释性。相反,Pathway Lasso引入了一个新的凸惩罚项,即Pathway Lasso惩罚,直接对路径效应进行正则化。这种方法解决了传统Lasso和其他凸正则化方法无法处理的乘积参数问题,因为路径效应通常表示为两个参数的乘积,这是一个非凸函数。通过Pathway Lasso惩罚,可以同时实现路径选择和路径效应估计,允许模型直接处理相关中介变量,提供更直接和简单的中介路径解释,尤其适用于分析多个大脑区域作为中介变量的情况。
Pathway Lasso的优势
在路径选择和估计准确性方面相较于其他方法具有以下优势
- 高路径选择准确性:在模拟数据和fMRI数据集上的应用表明,Pathway Lasso 提出的方法比其他方法具有更高的路径选择准确性。
- 低估计偏误:Pathway Lasso 方法在估计路径效应时表现出更低的偏差。
- 解决非凸性问题:Pathway Lasso 引入了一个新的凸惩罚,直接对乘积非凸函数进行正则化,解决了现有方法未处理的问题。
- 直接和明确的解释性:与使用线性组合(如主成分分析)的方法相比,Pathway Lasso 允许对每个中介路径进行更直接和更简单的解释。
- 处理相关中介变量:Pathway Lasso 允许直接建模相关中介变量,适合分析多个大脑区域作为中介的设置。
实现方法
随机生成单模态高维度中介分析数据
代码格式
modalityMediationDataGen(
n = 100,
p = 50,
sigmaY = 1,
sizeNonZero = c(3, 3, 4),
alphaMean = c(6, 4, 2),
alphaSd = 0.1,
betaMean = c(6, 4, 2),
betaSd = 0.1,
sigmaM1 = NULL,
gamma = 3,
generateLaplacianMatrix = FALSE,
seed = 20231201
)参数说明
n: 高维中介模型中的主体数量。
p: 高维中介变量的数量。
sigmaY: 因变量误差分布的标准差。
sizeNonZero: 非零中介变量的数量,生成大、中、小中介效应的模拟场景。
alphaMean, alphaSd: 中介变量与自变量之间效应的平均值和标准差向量。
betaMean, betaSd: 中介变量与因变量之间效应的平均值和标准差向量。
sigmaM1: 中介变量间误差分布的协方差矩阵,默认为对角矩阵。
gamma: 直接效应的真值。
generateLaplacianMatrix: 逻辑值,指定是否生成网络惩罚的拉普拉斯矩阵。
seed: 随机种子,默认为NULL以使用当前种子
返回结果解释
MediData: 高维中介模型的模拟数据。
MediPara: 中介效应和直接效应的真值。
Info: 输出包括随机种子、参数设置以及生成中介模型的拉普拉斯矩阵。
示例代码
## 生成分析数据
simuData <- modalityMediationDataGen(seed = 20231201)
str(simuData)
# 输出结果如下
# List of 3
# $ MediData:List of 3
# ..$ X : num [1:100, 1] 0 0 1 0 0 0 1 0 0 1 ...
# ..$ M1: num [1:100, 1:50] 1.023 -0.369 4.812 1.476 0.188 ...
# ..$ Y : num [1:100, 1] -10.27 6.54 175.08 -1.66 17.55 ...
# $ MediPara:List of 3
# ..$ alpha: num [1, 1:50] 5.99 5.99 6 4.11 4.17 ...
# ..$ beta : num [1:50, 1] 6.11 5.96 6.01 4.05 3.88 ...
# ..$ gamma: num [1, 1] 3
# $ Info :List of 4
# ..$ parameters :List of 7
# .. ..$ sigmaY : num 1
# .. ..$ sizeNonZero: num [1:3] 3 3 4
# .. ..$ alphaMean : num [1:3] 6 4 2
# .. ..$ alphaSd : num [1:3] 0.1 0.1 0.1
# .. ..$ betaMean : num [1:3] 6 4 2
# .. ..$ betaSd : num [1:3] 0.1 0.1 0.1
# .. ..$ sigmaM1 : num [1:50, 1:50] 1 0 0 0 0 0 0 0 0 0 ...
# ..$ trueValue :List of 1
# .. ..$ gamma: num [1, 1] 3
# ..$ laplacianMatrix: NULL
# ..$ seed : num 20231201
simuData <- modalityMediationDataGen(seed = 20231201, generateLaplacianMatrix = TRUE)
str(simuData)
simuData <- modalityMediationDataGen(n = 50, p = 1000, seed = 20231201)
str(simuData)交叉验证:cvSingleModalityAdmm
通过设置`numFolds`参数进行交叉验证,可以评估不同惩罚参数下的模型性能,帮助选择最佳模型
`交叉验证的结果,用于评估不同参数组合下Pathway Lasso惩罚方法的效果。输出结果是一个表格,其中包含以下列:
1. **rho**:这是ADMM算法中的ρ参数的候选值,它影响算法的收敛速度和解的质量。
2. **lambda1a**:Pathway Lasso惩罚中的λ1a参数的候选值,L1 范数惩罚中介变量和自变量之间的影响。
3. **lambda1b**:Pathway Lasso惩罚中的λ1b参数的候选值,中介变量和因变量之间影响的 L1 范数惩罚。
4. **lambda1g**:Pathway Lasso惩罚中的λ1g参数的候选值,直接效应的 L1 范数惩罚。默认值为 10 以解决高估问题。
5. **kappa**:Pathway Lasso惩罚的L1范数参数,控制路径正则化的具体形式。控制了路径结构的稀疏性,当kappa较小时,惩罚的作用更加平滑,有利于保留更多的特征;当kappa较大时,惩罚更加集中,有利于稀疏性,即更多特征被剔除。
6. **nu**:Pathway Lasso惩罚的L2范数参数,同样影响路径正则化。nu: 控制了路径结构中特征之间的相关性,当nu较小时,路径结构更加独立,有利于减少特征之间的相关性;当nu较大时,更多的特征将共享相同的路径,有助于保留相关性较强的特征。
7. **measure**:评估指标,默认均方根误差(RMSE),用于衡量预测结果与真实结果之间的差异。低的RMSE值通常意味着更好的模型性能,因为这表示预测误差更小。通过比较这些结果,可以选取最优的参数组合来构建最终模型。
8. lambda2a、lambda2b: 是 Pathway Lasso 方法中额外引入的惩罚项的参数。它们可以控制特征之间的相关性,帮助更好地保留特征间的相关性信息。
lambda2a:L2 范数惩罚中介变量和自变量之间的影响lambda2b:中介变量和因变量之间影响的 L2 范数惩罚
# 2种不同的惩罚方法
## 1.使用交叉验证进行 ElasticNet 惩罚参数调优
# 执行交叉验证
cvElasticNetResults <- cvSingleModalityAdmm(
X = simuData$MediData$X, # 独立变量的数据矩阵(暴露/治疗/组)
Y = simuData$MediData$Y, # 因变量的数据向量(结果响应)
M1 = simuData$MediData$M1, # 单模态中介变量
numFolds = 5, # 交叉验证的折数
typeMeasure = "rmse", # 评估指标类型,默认为均方根误差
rho = c(0.9, 1, 1.1), # rho 参数的候选值序列
lambda1a = c(0.1, 0.5, 1), # lambda1a 参数的候选值序列
lambda1b = c(0.1, 0.3), # lambda1b 参数的候选值序列
lambda1g = c(1, 2), # lambda1g 参数的候选值序列
lambda2a = c(0.5, 1), # lambda2a 参数的候选值序列
lambda2b = c(0.5, 1), # lambda2b 参数的候选值序列
penalty = "ElasticNet" # 使用 ElasticNet 惩罚
)
# 输出结果:
> cvElasticNetResults
rho lambda1a lambda1b lambda1g lambda2a lambda2b measure
[1,] 0.9 0.1 0.1 1 0.5 0.5 18.23108
[2,] 1.0 0.1 0.1 1 0.5 0.5 18.32964
[3,] 1.1 0.1 0.1 1 0.5 0.5 18.17303
[4,] 0.9 0.5 0.1 1 0.5 0.5 17.77722
[5,] 1.0 0.5 0.1 1 0.5 0.5 17.78040
[6,] 1.1 0.5 0.1 1 0.5 0.5 17.77446
[7,] 0.9 1.0 0.1 1 0.5 0.5 17.80479
[到达getOption("max.print") -- 略过很多行]]
attr(,"class")
[1] "cvSingleModalityAdmm"
--------------------------------------------------------------------------
# 2. 使用交叉验证进行 Pathway Lasso 惩罚参数调优(lambda2a, lambda2b 未调整)
# 执行交叉验证
cvPathwayLassoResults <- cvSingleModalityAdmm(
X = simuData$MediData$X, # 独立变量的数据矩阵(暴露/治疗/组)
Y = simuData$MediData$Y, # 因变量的数据向量(结果响应)
M1 = simuData$MediData$M1, # 单模态中介变量
numFolds = 5, # 交叉验证的折数
typeMeasure = "rmse", # 评估指标类型,默认为均方根误差
rho = c(0.9, 1, 1.1), # rho 参数的候选值序列
lambda1a = c(0.1, 0.5, 1), # lambda1a 参数的候选值序列
lambda1b = c(0.1, 0.3), # lambda1b 参数的候选值序列
lambda1g = c(1, 2), # lambda1g 参数的候选值序列
lambda2a = 1, # 给定 lambda2a 参数值
lambda2b = 1, # 给定 lambda2b 参数值
penalty = "PathwayLasso", # 使用 Pathway Lasso 惩罚
penaltyParameterList = list(kappa = c(0.5, 1), nu = c(1, 2)) # 惩罚参数列表,包括 kappa 和 nu
)
# 输出结果:
cvPathwayLassoResults
rho lambda1a lambda1b lambda1g kappa nu measure
[1,] 0.9 0.1 0.1 1 0.5 1 19.46943
[2,] 1.0 0.1 0.1 1 0.5 1 19.37725
[3,] 1.1 0.1 0.1 1 0.5 1 19.40920
[4,] 0.9 0.5 0.1 1 0.5 1 19.49747
[到达getOption("max.print") -- 略过很多行]]
attr(,"class")
[1] "cvSingleModalityAdmm"将权矩阵转换为拉普拉斯矩阵的辅助函数:weightToLaplacian()
# 将权矩阵转换为拉普拉斯矩阵的辅助函数:weightToLaplacian()
set.seed(20231201) # 设置随机数种子
p <- 5 # 设置节点数
W <- matrix(0, nrow = p, ncol = p) # 初始化权矩阵
W[lower.tri(W)] <- runif(p*(p-1)/2, 0, 1) # 生成随机权的下三角矩阵
W[upper.tri(W)] <- t(W)[upper.tri(W)] # 使权矩阵对称
diag(W) <- 1 # 对角线元素设为1
W
# 输出结果如下
# [,1] [,2] [,3] [,4] [,5]
# [1,] 1.0000000 0.1623753 0.48119340 0.4406640 0.36219565
# [2,] 0.1623753 1.0000000 0.41138920 0.1344408 0.64471664
# [3,] 0.4811934 0.4113892 1.00000000 0.5306324 0.08042435
# [4,] 0.4406640 0.1344408 0.53063239 1.0000000 0.85450197
# [5,] 0.3621956 0.6447166 0.08042435 0.8545020 1.00000000
(L <- weightToLaplacian(W)) # 将权矩阵转换为拉普拉斯矩阵
# 输出结果如下
# [,1] [,2] [,3] [,4] [,5]
# [1,] 0.59124083 -0.06767837 -0.19443191 -0.16374871 -0.13501050
# [2,] -0.06767837 0.57499652 -0.16949748 -0.05094059 -0.24505056
# [3,] -0.19443191 -0.16949748 0.60058145 -0.19491464 -0.02963414
# [4,] -0.16374871 -0.05094059 -0.19491464 0.66218945 -0.28956112
# [5,] -0.13501050 -0.24505056 -0.02963414 -0.28956112 0.66007653
拟合高维单模态中介模型
根据cvSingleModalityAdmm的结果挑选最佳参数,拟合🔤高维单模态中介模型🔤
penalty方法
penalty方法有3种+ 各自对应的惩罚参数列表【penaltyParameterList】
- 默认为弹性网络 ElasticNet
- lambda1a, lambda1b, lambda1g, lambda2a, lambda2b
- 路径套索(PathywayLasso)
- kappa 路径 Lasso 的 L1 范数惩罚。
- nu 路径 Lasso 的 L2 范数惩罚
- 网络约束惩罚(Network)
- 需要应用于网络惩罚的拉普拉斯矩阵
确定独立性筛选 (SIS)
SIS:指定是否执行确定独立性筛选 (sure independence screening, SIS)
- SISThreshold,中介者目标降维的阈值。默认值为“2”,这会将维度减少到 2*n/log(n)。n代表样本量
输出结果
- gamma:🔤估计直接影响🔤
- alpha:🔤估计中介变量和自变量之间的影响。🔤
- beta:🔤估计中介变量和因变量之间的影响🔤
综合应用
1. ElasticNet 惩罚
## 生成经验数据
simuData <- modalityMediationDataGen(seed = 20231201, generateLaplacianMatrix = TRUE)
## ElasticNet 惩罚的参数估计
modelElasticNet <- singleModalityAdmm( X = simuData$MediData$X, Y = simuData$MediData$Y, M1 = simuData$MediData$M1, rho = 1, lambda1a = 1, lambda1b = 0.1, lambda1g = 2, lambda2a = 1, lambda2b = 1, penalty = "ElasticNet" )
# 拟合并预测
fitted(modelElasticNet)
predict(modelElasticNet, matrix(c(0, 1), ncol=1))
# SIS独立性筛选
simuData <- modalityMediationDataGen(n = 50, p = 1000, seed = 20231201)
modelElasticNetSIS <- singleModalityAdmm( X = simuData$MediData$X, Y = simuData$MediData$Y, M1 = simuData$MediData$M1, rho = 1, lambda1a = 1, lambda1b = 0.1, lambda1g = 2, lambda2a = 1, lambda2b = 1, penalty = "ElasticNet", SIS = TRUE )
fitted(modelElasticNetSIS)
predict(modelElasticNetSIS, matrix(c(0, 1), ncol=1))2. 使用拉普拉斯矩阵进行网络惩罚的参数估计
# 1.使用模拟数据中的拉普拉斯矩阵
simuData <- modalityMediationDataGen(seed = 20231201, generateLaplacianMatrix = TRUE)
modelNetwork <- singleModalityAdmm( X = simuData$MediData$X, Y = simuData$MediData$Y, M1 = simuData$MediData$M1, rho = 1, lambda1a = 1, lambda1b = 0.1, lambda1g = 2, lambda2a = 1, lambda2b = 1, penalty = "Network", penaltyParameterList = list(laplacianMatrix = simuData$Info$laplacianMatrix) )
# 2. 自定义的拉普拉斯矩阵
set.seed(20231201)
p <- ncol(simuData$MediData$M1)
W <- matrix(0, nrow = p, ncol = p)
W[lower.tri(W)] <- runif(p*(p-1)/2, 0, 1)
W[upper.tri(W)] <- t(W)[upper.tri(W)]
diag(W) <- 1
L <- weightToLaplacian(W)
modelNetwork <- singleModalityAdmm( X = simuData$MediData$X, Y = simuData$MediData$Y, M1 = simuData$MediData$M1, rho = 1, lambda1a = 1, lambda1b = 0.1, lambda1g = 2, lambda2a = 1, lambda2b = 1, penalty = "Network", penaltyParameterList = list(laplacianMatrix = L) )3. Pathway Lasso 惩罚的参数估计
simuData <- modalityMediationDataGen(seed = 20231201, generateLaplacianMatrix = TRUE)
modelPathwayLasso <- singleModalityAdmm( X = simuData$MediData$X, Y = simuData$MediData$Y, M1 = simuData$MediData$M1, rho = 1, lambda1a = 1, lambda1b = 0.1, lambda1g = 2, lambda2a = 1, lambda2b = 1, penalty = "PathwayLasso", penaltyParameterList = list(kappa = 1, nu = 2) )