本博客以一种较为少见的方式来解释WQS二分。

题目

首先，WQS二分用于解决什么问题？

我们先看一个伞兵题目：

有一个 $n$ 个数的数组 $a$。
求在 $a$ 中恰好选择 $m$ 个数的情况下，选择的数的和的最大值。

你现在看到了这个题目，你发现你不会排序，不会贪心。

你打算用另一种方式解决这题。

做法

我们定义 $g(x)$ 为恰好选择 $x$ 个数的情况下，选择的数的和的最大值。

经过观察，我们发现 $g(x)$ 是一个凸函数。

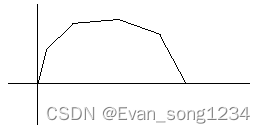
这表明，$g(x)$ 只有一个最大值（也就是把所有正数都取了的情况）。

但你取不到，因为他不一定是 $m$。

如果我们不考虑 $m$ 的限制，肯定会取这个最大值。

那么我们考虑如何做出改变使得不用考虑 $m$ 的限制。

考虑给选择数一个惩罚或奖励 $k$，我们每次选择一个数，答案就增加 $k$。（谁告诉你 $k$ 不能是负数了）

于是，这个函数 $g(x)$ 就转变成另一个函数 $f(x)=g(x)+kx$ 了。

显然，当 $k$ 取值增大，$f(x)$ 的最大值取值位置就往右移动。

当 $k$ 取值减少，$f(x)$ 最大值取值位置往左移动。

而我们能够轻易的对于每个 $k$ 计算 $f(x)$ 最大值取值位置和 $f(x)$ 最大值（$O(n)$）。

所以，我们可以二分 $k$，根据当前 $k$ 下 $f(x)$ 最大值取值位置与题目限制 $m$ 的大小关系来更改 $k$。

最终可以获得最大值取值位置为 $m$ 时的 $k$ 和 $f(m)$。

然后通过 $f(x)=g(x)+kx$，可以反推出 $g(m)=f(m)-km$。

做完了，$O(n\log n)$。我们震惊的发现时间复杂度和原做法没区别。