概述：

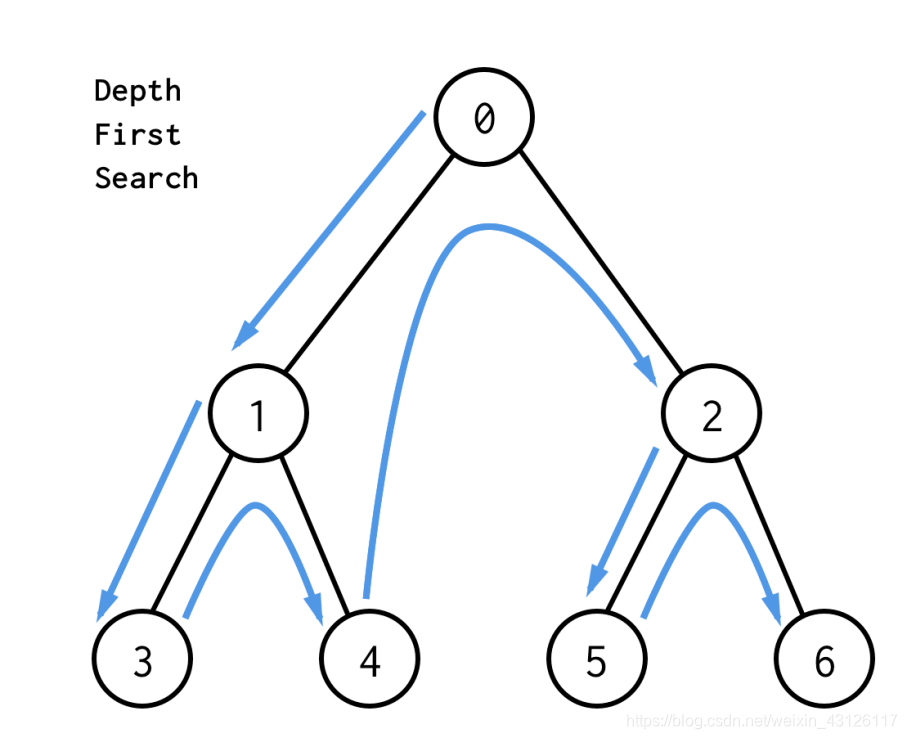
在我们刷算法的过程中肯定会想到暴力通过，暴力是不需要技巧的，在暴力算法中有一种枚举算法--深搜（深度搜索）dfs，其实在数据结构这门课程中我们是学过树的dfs深度优先算法的，但是我学的比较刻板，只能理解思想，代码也只能在树中能够实现，在算法题中很难想到怎么实现深搜。

个人对深搜的理解：

其实万变不离其宗，在算法题中我们还是把样例想成一颗树进行，进行向下分层。其实深搜也是递归的调用，递归先要设置函数的结束条件，再向下进行遍历调用。在深搜中我们还需要辅助数组标记数值的状态。

深搜模板：

void dfs(int step){
	if(结束条件)
	{
		输出解;
		return; 
	}
	for(int i=0;i<=枚举数;i++)
	{
		if(满足条件)
		{
			进行操作;
			更新状态位;
			dfs(step+1);
			恢复状态位 ; 
		}
	}
}

例题：

百闻不如一见，看一道题目加深理解：

题目描述

按照字典序输出自然数 11 到 nn 所有不重复的排列，即 nn 的全排列，要求所产生的任一数字序列中不允许出现重复的数字。

输入格式

一个整数 nn。

输出格式

由 1 \sim n1∼n 组成的所有不重复的数字序列，每行一个序列。

每个数字保留 55 个场宽。

输入输出样例

输入 #1复制

输出 #1复制

    1    2    3
    1    3    2
    2    1    3
    2    3    1
    3    1    2
    3    2    1

说明/提示

1≤n≤9。

# include <bits/stdc++.h>
using namespace std;
int n;
int a[10];
int st[10];
void dfs(int x)
{
	if(x==n+1)
	{
		for(int i=1;i<=n;i++)
		{
			cout<<setw(5)<<a[i];
		}
		cout<<endl;
		return ;
	}
	for(int i=1;i<=n;i++)
	{
		if(!st[i]){
		a[x]=i; 
		st[i]=1;
		dfs(x+1);
		st[i]=0;	
		}       //i=3  i=2

		
	}
}
int main()
{
	cin>>n;
	dfs(1);
 }