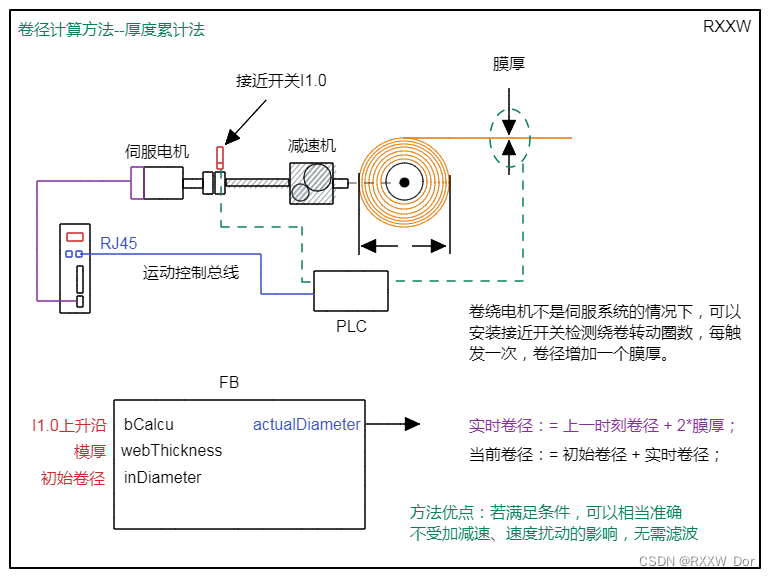
递归算法是常见的基础算法之一，阶乘、青蛙跳台、兔子算法等便是递归算法中典型的例子。

以6的阶乘为例，计算的过程如下图所示

Python代码实现如下：

def jiecheng(n):
    if n == 1:
        result = 1
    else:
        result = n * jiecheng(n - 1)
    return result

print(jiecheng(6))

题目：有一只青蛙，想要跳到最高的台阶上看风景，台阶比较高，小青蛙每次只能跳一阶或两阶，如果台阶一共有 N 阶，请问小青蛙有多少种跳法？
分析：
当台阶数为1时，跳法为1，即（1）；
当台阶数为2时，跳法为2，即（1）、（1，2）；
当台阶数为3时，跳法为3，即（1、1、1）、（1、2）、（2、1）；
当台阶数为4时，跳法为5，即（1、1、1、1）、（1、1、2）、（1、2、1）、（2、1、1）、（2、2）；
当台阶数为5时，跳法为8，即（1、1、1、1、1）、（1、1、1、2）、（1、1、2、1）、（1、2、1、1、）、（1、2、2）、（2、2、1）、（2、1、2）、（2、1、1、1）…
由此可以得出，台阶数为N时，跳法为（N-1)+(N-2)，即1、2、3、5、8…n斐波那契数列。
Python代码实现：

def frog(n):
    if n == 1 or n == 2:
        result = n
    else:
        result = frog(n - 1) + frog(n - 2)
    return result


print(frog(6))

题目：有一对兔子，3个月起每个月都生一对兔子，小兔子长到第三个月后每个月又生一对兔子，假如兔子都不死，问N个月的兔子总对数为多少？
分析：兔子从出生后三个月后每个月就会生出一对兔子，假设将兔子分为小中大三种， 第一个月的兔子为小兔子，第二个月为中兔子，第三个月之后就为大兔子，那么第一个月分别有1、0、0，第二个月分别为0、1、0，第三个月分别为1、0、1，第四个月分别为,1、1、1，第五个月分别为2、1、2，第六个月分别为3、2、3，第七个月分别为5、3、5…… 兔子总对数分别为：1、1、2、3、5、8、13…… 即为斐波那契数列，N个月的兔子总和即为斐波那契数列前N项之和。
Python代码实现：

def rabbit(n):
    if n == 1 or n == 2:
        result = 1
    else:
        result = rabbit(n - 1) + rabbit(n - 2)
    return result


def sum_rabbit(m):
    add = 0
    for i in range(1, m + 1):
        add += rabbit(i)
    return add


print(rabbit(4))
print(sum_rabbit(4))