PCB结构和谐振（一）

PCB结构和谐振（二）

仿真研究

在本节中，我们首先对玻璃束的随机分布进行了简单的模拟研究。然后我们利用这些实验结论来简化常用的玻璃布3D结构。最后，这种简化的结构用于研究复杂层压板和两个周期性布局设计的谐振。

玻璃束的随机分布

我们认为玻璃纤维的随机分布导致了上一节中提到的现象（1）和（2）。为了验证这一推论，我们基于图 2 中的阻抗不连续模型进行了简单的模拟。玻璃束的随机分布导致周期长度的随机分布。因此，我们将周期长度随机分布为统计高斯分布，平均值为 2cm，标准差为 0.2cm。

图 17 比较了均匀分布和随机分布的 SDD21 的大小。周期长度的随机分布有效地削弱了谐振的强度，尤其是除了第一次谐振之外的那些。除此之外，其他能量抖动出现在原始谐振附近。这个仿真结果验证了我们之前的推断。

对3D玻布模型的简化

如图5（a）所示，玻璃布的结构非常复杂。图 18 所示的典型 3D 模型通常用于描述编织结构，包括经纱和纬纱玻璃束。然而，在上一篇中获得的谐振通常可以通过等式 1 和 4 预测，并且是由经向的 E 玻璃束引起的。有时可以忽略纬向玻璃（MS-玻璃）束。例如，如果我们要模拟走线和弯曲成 10 度角的情况，模拟的频率范围是 10MHz 到 40GHz，我们可以先使用等式 1 和等式 4 来预测其谐振频率，如在表2中。我们只需要考虑模型中经向玻璃束的结构，因为即使是纬向玻璃束也会引起明显的谐振，其第一个共振频率将超过40GHz。

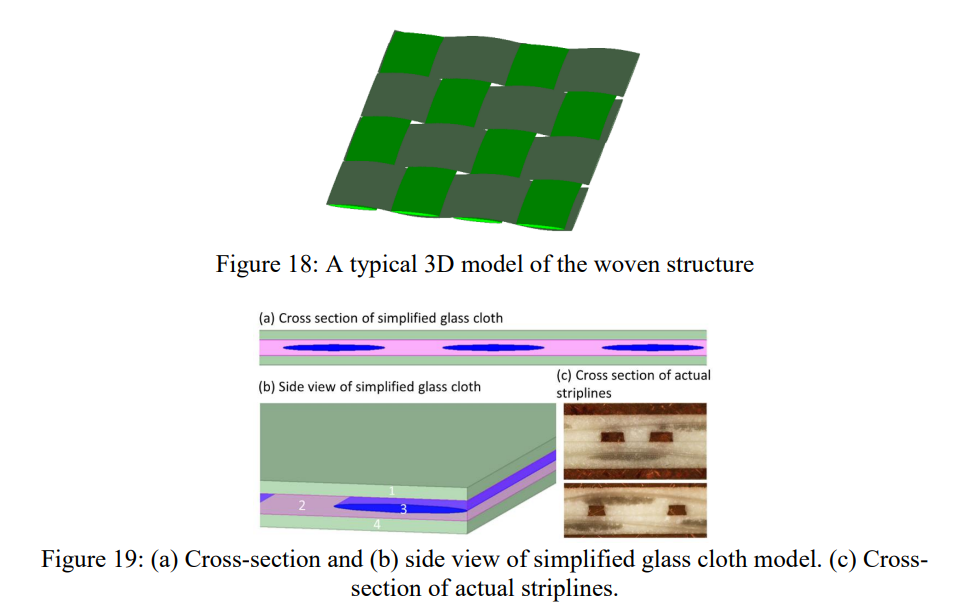
通过这种方式，我们将编织结构简化为图 19 (a) 和 (b) 所示的模型。四个区域构成了这个模型。

区域 1 和 4 代表树脂，其 Dk 值是从材料供应商处获得的。区域 3 代表引起谐振的经向玻璃束，其 Dk 值由 Intel 的方法[9]获得。区域 2 代表树脂和纬向玻璃束的混合物，其 Dk 值通过加权两种组分的体积比来平均。如果我们用这个玻璃布模型来组成一个核心结构，不同区域的厚度给出如下：

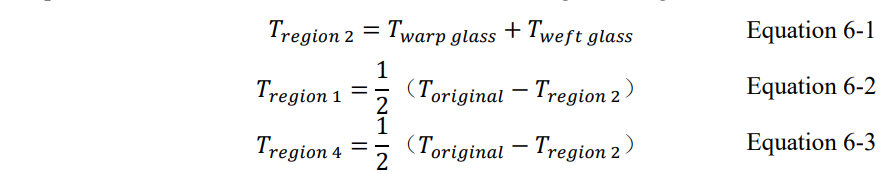
其中，Tregion1/Tregion2/Tregion4分别代表区域1/2/3的厚度。Toriginal代表加工前core的厚度，Twarp glass和Tweft glass分别代表经向和纬向玻璃束的厚度。

值得注意的是，我们已经考虑到了该模型中树脂流动的影响。在图19 c中，PP中的玻璃束比core中的玻璃束离走线更近，这是因为PP中的部分树脂被用于填充PCB的空缺区域。在一层PP中，假设区域4更接近于走线，Tregion4可以用过公式6-4计算：

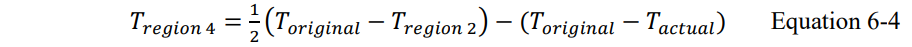
Tactual表示加工后PP的实际厚度。如果Tregion4小于0，那就在模型中取消掉区域4.

图19 a中的玻璃束分布是随机的，这种随机分布对应的平均值和标准差很容易从实际截面中统计得到。

复杂压合仿真

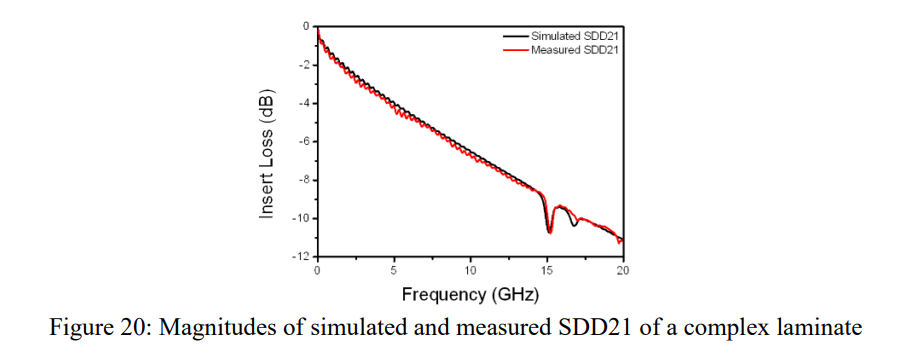
基于上面简化的玻璃布模型，我们模拟了一个复杂的层压板，如图 12 所示。由于蚀刻因素的存在会影响电磁场的分布，我们还根据实际横截面对差分对进行了建模。我们在图 20 中比较了模拟的 SDD21 和测量的 SDD21。通过考虑这些因素，包括主要玻璃束、玻璃束的非均匀分布、树脂流动和蚀刻因素，模拟和实验结果非常吻合。

两种周期性layout设计的仿真

这里我们仿真了两种周期性的layout设计，对于每种设计，分别涵盖了理想模型（无编织结构）和简易3D模型（包含编织结构）。在理想模型中，除了没有编织结构，走线层的Dk也是一致的。

（1）W型走线

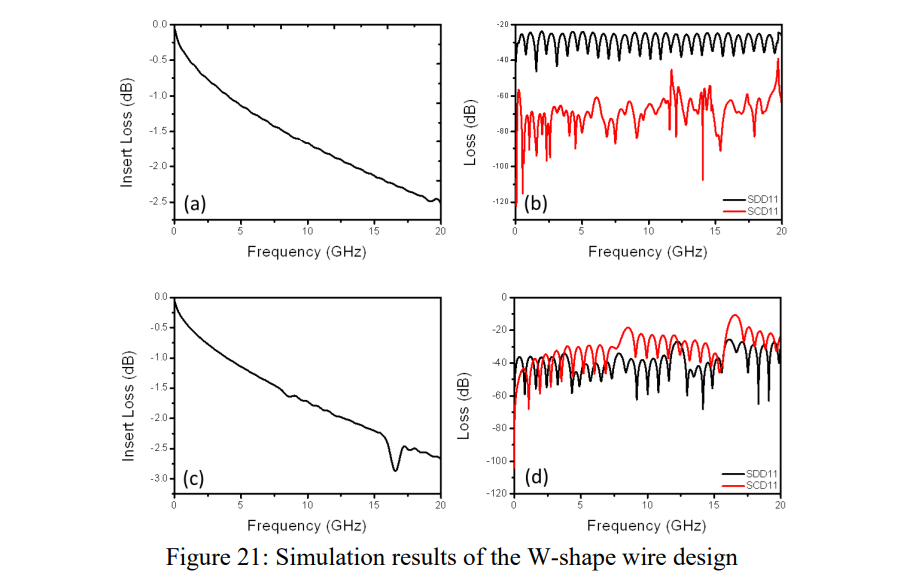
W型走线的周期设置为1cm，走线和经向夹角为10°。为了降低仿真复杂性，仅仅仿真单张1078玻布情况。下图a和b分别展示了理想模型中的SDD21/SDD11/SCD11。在理想模型中并未发现明显的谐振，下图c和d是简易3D模型中的SDD21/SDD11/SCD11，结果中发现了两处明显的谐振。但是和实测有差异的是在4GHz左右的第一个谐振点（由不连续性2导致），在仿真中并不明显，我们猜测，由于制造公差，直线段和弯曲段之间的走线宽度存在一些差异。

（2）蛇形线

蛇形线长度周期设置为0.7cm，其他仿真细节和W型走线一致。下图a和b是理想模型的SDD21/SDD11/SCD11，图c和d是简易3D模型的SDD21/SDD11/SCD11。两种模型都存在明显的谐振，这一点和W型走线不同。

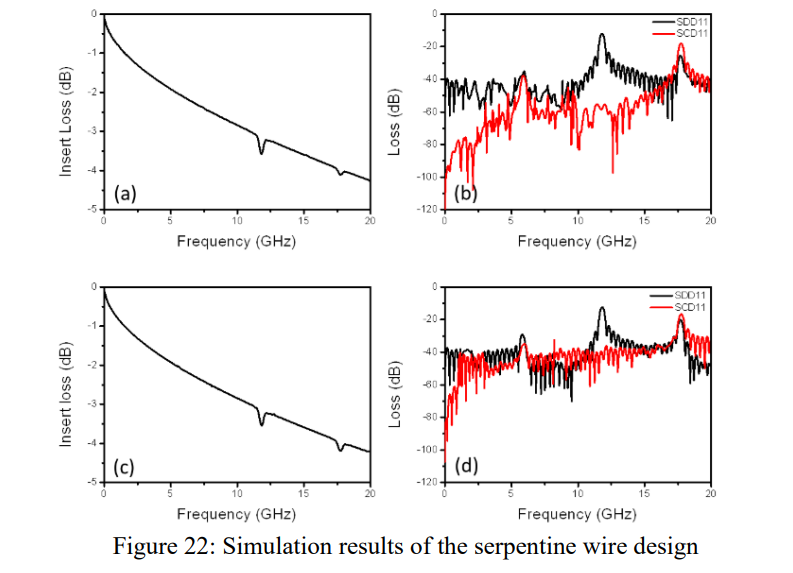
比较两种走线设计的仿真结果，可以发现蛇形线的谐振主要是由于走线设计本身，因为蛇形线的弯曲段通常比W形线的弯曲段大。由编织结构引起的 Dk 的不均匀分布会加剧谐振强度，尤其是对于 W 形线。W型走线因此更适合沿纬向走线（MS-glass），而蛇形线的周期长度需要仔细设计，使谐振频率远离PCB的工作频率。

动态仿真

为了了解谐振对信号完整性的影响，使用第 3 节中获得的 S 参数以不同的旋转角度进行了动态模拟，并对眼高和眼宽进行了统计。下面的图 23 显示了不同旋转角度对应的眼高和眼宽的箱线图。使用的S参数对应图8(a)，使用的信号速率为25Gbps。归一化值是指实际值减去旋转 5 度的平均值。较大的归一化值表示较好的信号完整性。

当旋转角度为3度和5度时，对应的谐振频率为9.83GHz和16.38GHz，接近信号工作频率12.5GHz。而谐振引起的额外能量损失显然会导致眼图质量的恶化。该仿真结果表明，由周期性结构引起的谐振会影响信号完整性。

结论

在本文中，两个简单的skew和阻抗不连续模型被用来说明由周期性结构引起的谐振频率与其周期长度有关，而与不连续形成的机制关系不大。论文总结了周期长度与谐振的关系，并通过数值方法计算了玻璃布的Dk分布，并通过直线差分对与玻璃束的位置关系阐述了周期的产生。

对于直线，最好沿纬向（MSglass）布线差分对，而不是沿经向（E-glass）布线。对于沿着经线的这些情况，随着相对于经线的旋转角度变大，共振以更大的谐振强度移动到更高的频率。我们还发现，玻璃束的随机分布有效地削弱了谐振的强度，尤其是除了第一次谐振之外的那些。根据实验结果，增加玻璃布的数量和使差分对的间距值更接近玻璃束的间距值有望成为削弱谐振强度的有效方法。对于两个周期性布局设计，谐振被证明与设计周期的长度有关。给出了三种不连续性来解释周期是如何形成的。

在仿真研究中，给出了玻璃束随机分布的简化玻璃布模型。根据实验结果，我们简化了玻璃布模型，忽略了这些对相关谐振没有贡献的玻璃束。在这个模型中，我们还考虑了蚀刻因素和生产加工引起的树脂流动。仿真所需的所有参数都可以轻松地从材料供应商和实际横截面获得。我们模拟了复杂的层压板，实验和模拟非常吻合。两种布局设计的仿真结果证明，编织结构引起的 Dk 分布不均匀会加剧导线设计引起的谐振，尤其是 W 形导线。 W型线因此更适合沿纬向走线（MS-glass），而蛇形线的周期长度需要仔细设计，使谐振频率远离PCB的工作频率。

最后，动态仿真表明，由周期性结构引起的谐振会影响信号完整性。