引言

从本节开始，将介绍深度信念网络。

深度信念网络

深度信念网络(Deep Belief Network,DBN)是杰弗里·辛顿(Geoffrey Hinton)于2006年提出的模型，并正式提出了深度学习的概念。
在当时，将深度信念网络应用在分类问题中，其超过了当时主流的支持向量机 + 核技巧的分类效果。

在Sigmoid信念网络中介绍过，信念网络指的就是贝叶斯网络，也就是有向图模型。
但实际上，和$\text{Sigmoid}$信念网络不同，深度信念网络是一个混合模型(Hybrid Model)：

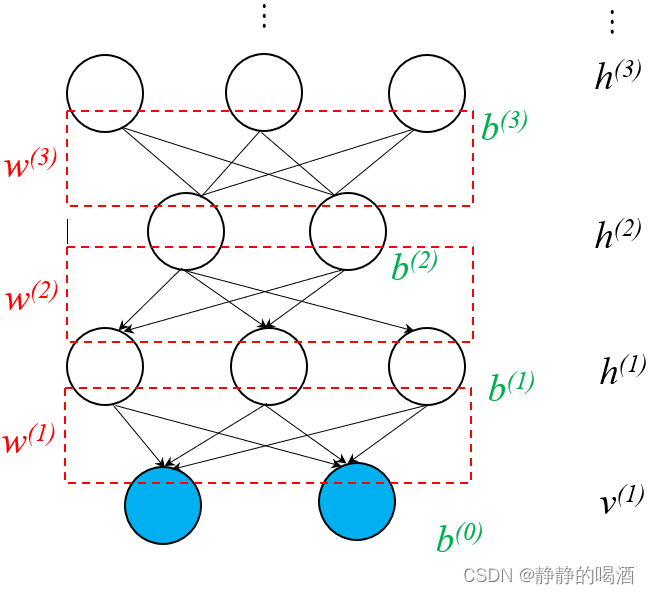
其中，$v$表示观测变量所在层(输入部分)，$h^{(1)},h^{(2)},h^{(3)}$分别表示不同隐藏层对应的编号。从上图中可以看出，$v^{(1)},h^{(1)},h^{(2)}$三层明显是一个$\text{Sigmoid}$信念网络；而$h^{(2)},h^{(3)}$两层则是受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)。
当然这里仅描述了一层受限玻尔兹曼机和一层$\text{Sigmoid}$信念网络的组合现象，实际上可以通过对受限玻尔兹曼机的堆叠(Stacking RBM)向更深层次进行延伸。
并且它也是一个基于深度学习的概率生成模型，它对应的数据同样是不包含标签信息的。至此，观察一下该模型的定义。

场景构建

为了更好地描述定义，我们对各符号进行设定：

• 各层之间的权重信息(图中的红色虚线部分)分别使用${\mathcal{W}}^{(1)},{\mathcal{W}}^{(2)},{\mathcal{W}}^{(3)}$进行表示；
• 深度信念网络中每一层均包含偏置项信息，定义从$v^{(1)},h^{(1)},h^{(2)},h^{(3)}$顺序对应的偏置分别表示为$b^{(0)},b^{(1)},b^{(2)},b^{(3)}$(图中的绿色部分)；
• 由于上标已经被占用，因此这里不同于之前对于样本的定义$v^{(i)}\in \mathcal{V}(i=1,2,\cdots ,N)$，这里仅使用$v\in \mathcal{V}$来描述样本集合$\mathcal{V}$中的某一各具体样本。

深度信念网络的联合概率分布

上述示例中描述的所有结点均是随机变量，并且除了观测变量是样本集合给定的之外，其余所有变量均是隐变量。其分布和玻尔兹曼机、受限玻尔兹曼机、$\text{Sigmoid}$信念网络相同，所有随机变量均服从伯努利分布：
这里直接使用$v^{(1)}$表示观测变量层中的所有随机变量结点组成的集合，其余层均同理。$\mathcal{D}$表示观测变量结点的数量。
v ( 1 ) = { v 1 ( 1 ) , v 2 ( 1 ) , ⋯   , v D ( 1 ) } ∈ { 0 , 1 } D v^{(1)} = \left\{v_1^{(1)},v_2^{(1)},\cdots, v_{\mathcal D}^{(1)}\right\} \in \{0,1\}^{\mathcal D} v(1)={v1(1)​,v2(1)​,⋯,vD(1)​}∈{0,1}D

至此，示例中所有随机变量(隐变量、观测变量)的联合概率分布可表示为：
将观测变量、隐变量分开。
$$\begin{array}{rl}\mathcal{P}(v^{(1)},h^{(1)},h^{(2)},h^{(3)})& =\mathcal{P}(v^{(1)}\mid h^{(1)},h^{(2)},h^{(3)})\cdot \mathcal{P}(h^{(1)},h^{(2)},h^{(3)})\end{array}$$

• 通过观察，观测变量集合$v^{(1)}$仅和隐变量集合$h^{(1)}$相关，和其他隐变量集合$h^{(2)},h^{(3)}$之间条件独立。因此，可以将上式化简为：
  这明显是‘贝叶斯网络’中的顺序结构：在$h^{(1)}$可观测的条件下，$v^{(1)}$与$h^{(2)},h^{(3)}$之间条件独立。
  $$\mathcal{P}(v^{(1)},h^{(1)},h^{(2)},h^{(3)})=\mathcal{P}(v^{(1)}\mid h^{(1)})\cdot \mathcal{P}(h^{(1)},h^{(2)},h^{(3)})$$
  同理，关于联合概率分布$P(h^{(1)},h^{(2)},h^{(3)})$，$h^{(1)}$仅和$h^{(2)}$之间存在关联关系。因而它的联合概率分布可表示为：
  此时，不同于$v^{(1)}$和$h^{(1)}$之间的关联关系，此时的模型结构是‘混合模型’，但是对条件独立性并不影响。
  $$\begin{array}{rl}\mathcal{P}(h^{(1)},h^{(2)},h^{(3)})& =\mathcal{P}(h^{(1)}\mid h^{(2)},h^{(3)})\cdot \mathcal{P}(h^{(2)},h^{(3)})\\ & =\mathcal{P}(h^{(1)}\mid h^{(2)})\cdot \mathcal{P}(h^{(2)},h^{(3)})\end{array}$$
  最终，联合概率分布$\mathcal{P}(v^{(1)},h^{(1)},h^{(2)},h^{(3)})$表示为：
  $$\mathcal{P}(v^{(1)},h^{(1)},h^{(2)},h^{(3)})=P(v^{(1)}\mid h^{(1)})\cdot \mathcal{P}(h^{(1)}\mid h^{(2)})\cdot \mathcal{P}(h^{(2)},h^{(3)})$$
• 观察等式右侧，其中$\mathcal{P}(v^{(1)}\mid h^{(1)}),\mathcal{P}(h^{(1)}\mid h^{(2)})$均表示基于$\text{Sigmoid}$信念网络下关于随机变量集合的后验概率分布，以$v^{(1)},h^{(1)}$之间的关联关系为例，$h^{(1)}$中的任意结点指向$v^{(1)}$，其组成的关联关系均属于同父结构，因此实际上，$v^{(1)}$中任意观测变量结点之间在$h^{(1)}$可观测的条件下均条件独立。因此，$\mathcal{P}(v^{(1)}\mid h^{(1)})$可表示为：
  $$\mathcal{P}(v^{(1)}\mid h^{(1)})=\prod _{i=1}^{\mathcal{D}}\mathcal{P}(v_i^{(1)}\mid h^{(1)})$$
  同理，$\mathcal{P}(h^{(1)}\mid h^{(2)})$也可表示为：
  这里${\mathcal{P}}^{(1)}$表示随机变量集合$h^{(1)}$中包含的随机变量的数量。
  $$\mathcal{P}(h^{(1)}\mid h^{(2)})=\prod _{j=1}^{{\mathcal{P}}^{(1)}}\mathcal{P}(h_j^{(1)}\mid h^{(2)})$$
  至此，$\mathcal{P}(v^{(1)},h^{(1)},h^{(2)},h^{(3)})$可展开为：
  $$\mathcal{P}(v^{(1)},h^{(1)},h^{(2)},h^{(3)})=\prod _{i=1}^{\mathcal{D}}\mathcal{P}(v_i^{(1)}\mid h^{(1)})\cdot \prod _{j=1}^{{\mathcal{P}}^{(1)}}\mathcal{P}(h_j^{(1)}\mid h^{(2)})\cdot \mathcal{P}(h^{(2)},h^{(3)})$$
• 继续观察，$\mathcal{P}(v_i^{(1)}\mid h^{(1)})$要如何进行表示呢？观察下图：
  
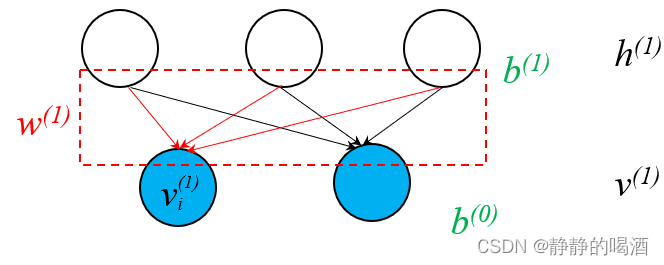
  根据Sigmoid信念网络的定义，后验概率$\mathcal{P}(v_i^{(1)}\mid h^{(1)})$可表示为：
  ${\mathcal{W}}_{h^{(1)}\to v_i^{(1)}}$表示$h^{(1)}$随机变量集合中的各隐变量结点指向$v_i^{(1)}$的权重信息，上图中的红色线部分。
  $$\mathcal{P}(v_i^{(1)}\mid h^{(1)})=\text{Sigmoid}\left\{{\left[{\mathcal{W}}_{h^{(1)}\to v_i^{(1)}}\right]}^T{h}^{(1)}+b_i^{(0)}\right\}{\left[{\mathcal{W}}_{h^{(1)}\to v_i^{(1)}}\right]}_{{\mathcal{P}}^{(1)}\times 1}\in {\mathcal{W}}^{(1)}$$
  同理，$\mathcal{P}(h_j^{(1)}\mid h^{(2)})$可表示为：
  $$\mathcal{P}(h_j^{(1)}\mid h^{(2)})=\text{Sigmoid}\left\{{\left[{\mathcal{W}}_{h^{(2)}\to h_j^{(1)}}\right]}^T{h}^{(2)}+b_j^{(1)}\right\}{\left[{\mathcal{W}}_{h^{(2)}\to h_j^{(1)}}\right]}_{{\mathcal{P}}^{(2)}\times 1}\in {\mathcal{W}}^{(2)}$$
  而最终$\mathcal{P}(h^{(2)},h^{(3)})$是关于受限玻尔兹曼机的联合概率分布，其结果可表示为：
  在受限玻尔兹曼机中介绍过，各层内的随机变量之间均条件独立，这里偏置项中乘的信息实际上就是各随机变量与自身之间关联关系信息。
  $$\mathcal{P}(h^{(2)},h^{(3)})=\frac{1}{\mathcal{Z}}\exp \left\{{\left[h^{(3)}\right]}^T{\mathcal{W}}^{(3)}\cdot h^{(2)}+{\left[h^{(2)}\right]}^T\cdot b^{(2)}+{\left[h^{(3)}\right]}^T{b}^{(3)}\right\}$$

至此，联合概率分布$\mathcal{P}(v^{(1)},h^{(1)},h^{(2)},h^{(3)})$可表示为：
$$\begin{array}{rl}& \mathcal{P}(v^{(1)},h^{(1)},h^{(2)},h^{(3)})=\prod _{i=1}^{\mathcal{D}}\mathcal{P}(v_i^{(1)}\mid h^{(1)})\cdot \prod _{j=1}^{{\mathcal{P}}^{(1)}}\mathcal{P}(h_j^{(1)}\mid h^{(2)})\cdot \mathcal{P}(h^{(2)},h^{(3)})\\ & \{\begin{array}{l}\mathcal{P}(v_i^{(1)}\mid h^{(1)})=\text{Sigmoid}\left\{{\left[{\mathcal{W}}_{h^{(1)}\to v_i^{(1)}}\right]}^T{h}^{(1)}+b_i^{(0)}\right\}{\left[{\mathcal{W}}_{h^{(1)}\to v_i^{(1)}}\right]}_{{\mathcal{P}}^{(1)}\times 1}\in {\mathcal{W}}^{(1)}\\ \mathcal{P}(h_j^{(1)}\mid h^{(2)})=\text{Sigmoid}\left\{{\left[{\mathcal{W}}_{h^{(2)}\to h_j^{(1)}}\right]}^T{h}^{(2)}+b_j^{(1)}\right\}{\left[{\mathcal{W}}_{h^{(2)}\to h_j^{(1)}}\right]}_{{\mathcal{P}}^{(2)}\times 1}\in {\mathcal{W}}^{(2)}\\ \mathcal{P}(h^{(2)},h^{(3)})=\frac{1}{\mathcal{Z}}\exp \left\{{\left[h^{(3)}\right]}^T{\mathcal{W}}^{(3)}\cdot h^{(2)}+{\left[h^{(2)}\right]}^T\cdot b^{(2)}+{\left[h^{(3)}\right]}^T{b}^{(3)}\right\}\end{array}\end{array}$$
对应的模型参数有：
θ = { W ( 1 ) , W ( 2 ) , W ( 3 ) , b ( 0 ) , b ( 1 ) , b ( 2 ) , b ( 3 ) } \theta = \{\mathcal W^{(1)},\mathcal W^{(2)},\mathcal W^{(3)},b^{(0)},b^{(1)},b^{(2)},b^{(3)}\} θ={W(1),W(2),W(3),b(0),b(1),b(2),b(3)}

下一节将介绍：为什么要设计乘多个$\text{RBM}$叠加的方式，或者说，叠加$\text{RBM}$的动机。

相关参考：
(系列二十七)深度信念网络1-背景介绍