作为机器学习的基础算法，SVM被反复提及，西瓜书、wiki都能查到详细介绍，但是总是觉得还差那么点，于是决定自己总结一下。

一、什么是SVM？

1、解决什么问题？

SVM，最原始的版本是用于最简单的线性二分类问题。当我们被给了一个新的数据点，其形式是一个p-维的向量，我们想知道它应该属于被一个（p-1）-维超平面分开的两半中哪一半。那么我们就想要通过已有数据找到“最有代表性的”超平面。这个超平面就是我们的分类标准。因为我们用到的是超平面而不是曲面，所以这是一个线性的问题。（加入核方法等可以改进为非线性分类）

2、怎么找超平面？ 

以下是一个取p=2的示例图，从图里可以看出，有许多超平面可以对数据进行分类。（在二维，超平面就是一条直线，需要确定直线的斜率和截距。）最佳超平面的一个合理选择是代表两个类别之间最大分离度或边际的超平面。因此，我们在选择超平面时，要使它到两侧最近数据点的距离最大。如果存在这样一个超平面，它就被称为最大边际超平面（maximum-margin hyperplane），而它所定义的线性分类器就被称为最大边际分类器（maximum-margin classifier）；或者等同于最佳稳定性感知器（the perceptron of optimal stability）。【from wiki】

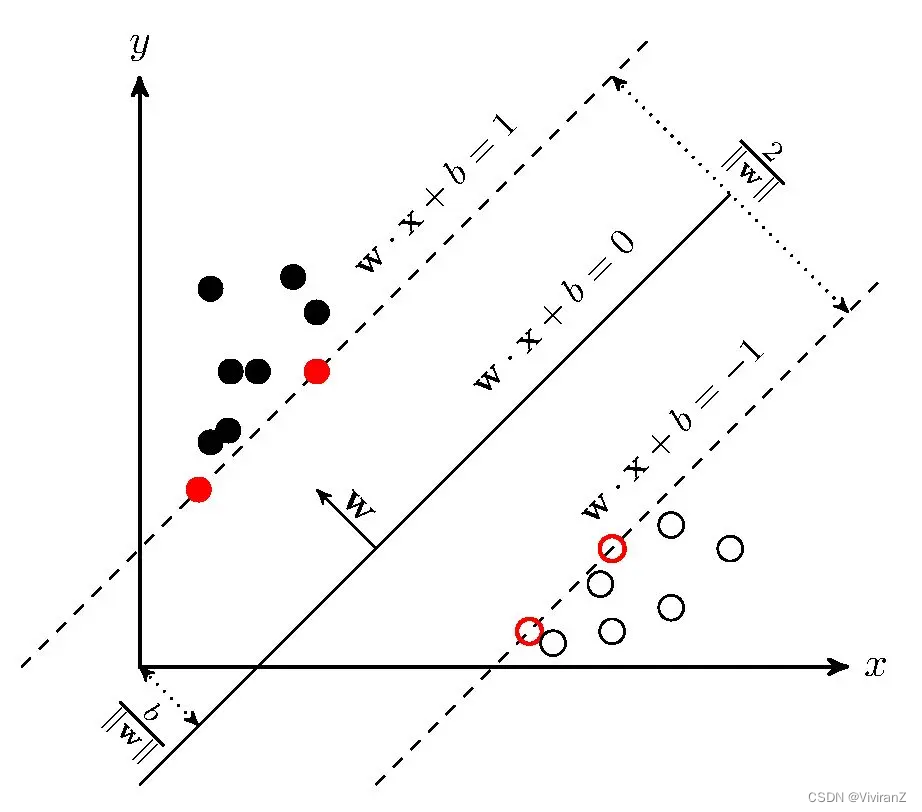
3、如何定义“最大距离”？

这一步博客 

支持向量机（SVM）——原理篇

里讲的很清晰了，基本也和西瓜书一致，我就不加赘述，简而言之，就是设出超平面的参数方程，代入求距离最近的点（min），再调整参数方程让最近的点距离尽量远（max）。

这种二次规划问题，一眼要用到拉格朗日乘子法求对偶问题，都是很基础的优化方法。

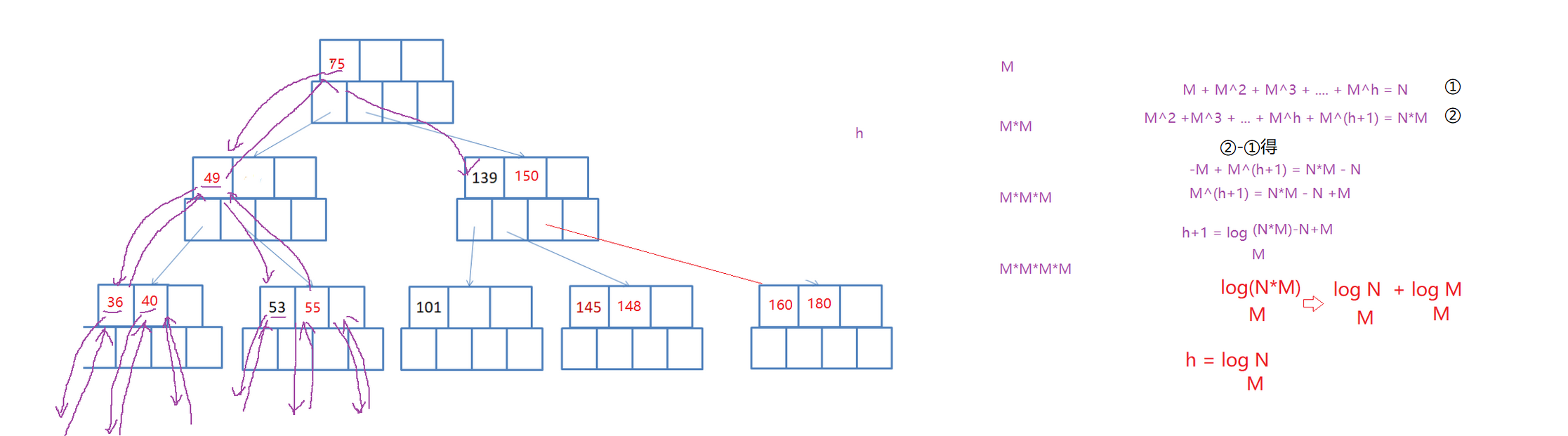
最终得到：

4、为什么叫“支持向量机”？

接下来这段话很简单但是清晰说明了SVM的本质：

 也就是说，最终我们只会考虑支持向量。

定义：距离超平面最近的几个训练样本点使得，这几个样本（由向量表示）被称为支持向量。两个异类支持向量到超平面的距离之和为，被称为间隔（margin）。

5、总结

SM，就是把分类问题或者回归问题，转化为基于已知的分类点求一个分类效果最好的分割超平面，进而可以用优化方法求解。

二、一些特殊的优化技巧？ 

1、核方法

a. 解决什么问题？

 基础的SVM需要假设所有样本是线性可分的，但是实际任务可能不是，而是需要一个曲面。

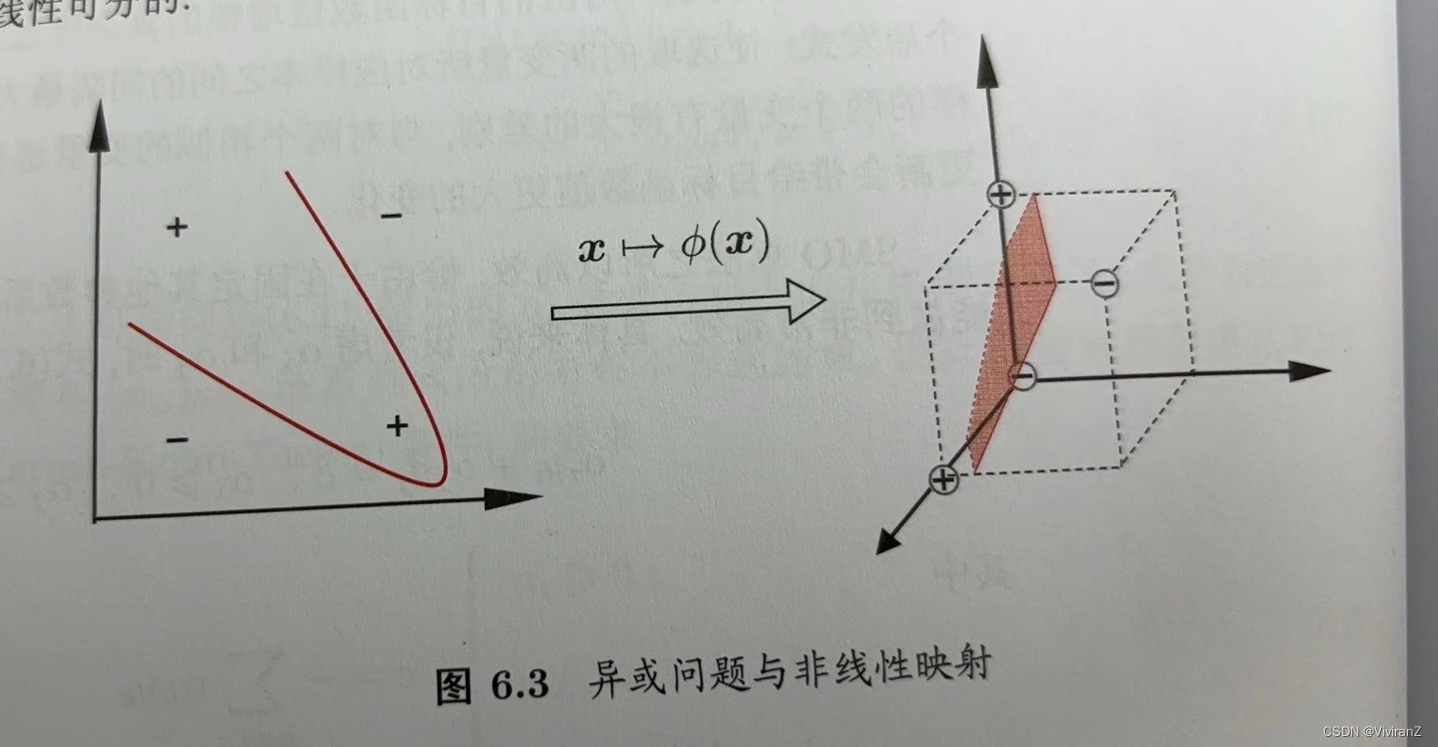
对这样的问题，可将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分：例如在图6.3中，若将原始的二维空间映射到一个合适的三维空间，就能找到一个合适的划分超平面，幸运的是，如果原始空间是有限维，即属性数有限，那么一定存在一个高维特征空间使样本可分。【引自西瓜书】

b.如何实现？

简单来说，就是找一个映射，把原本的数据映射到，通过推演我们发现

具体实现细节可以参考西瓜书或者以下博客： 
j​​​​​​​​​​​​​​浅入浅出核方法 (Kernel Method) - 知乎

2、软间隔

a. 解决什么问题？

即使我们用了核方法让原本不是线性可分的数据变得貌似线性可分，我们也不知道是不是过拟合了，缓解方法之一就是允许算法在一些样本上出错、也就是把硬间隔变成软间隔。

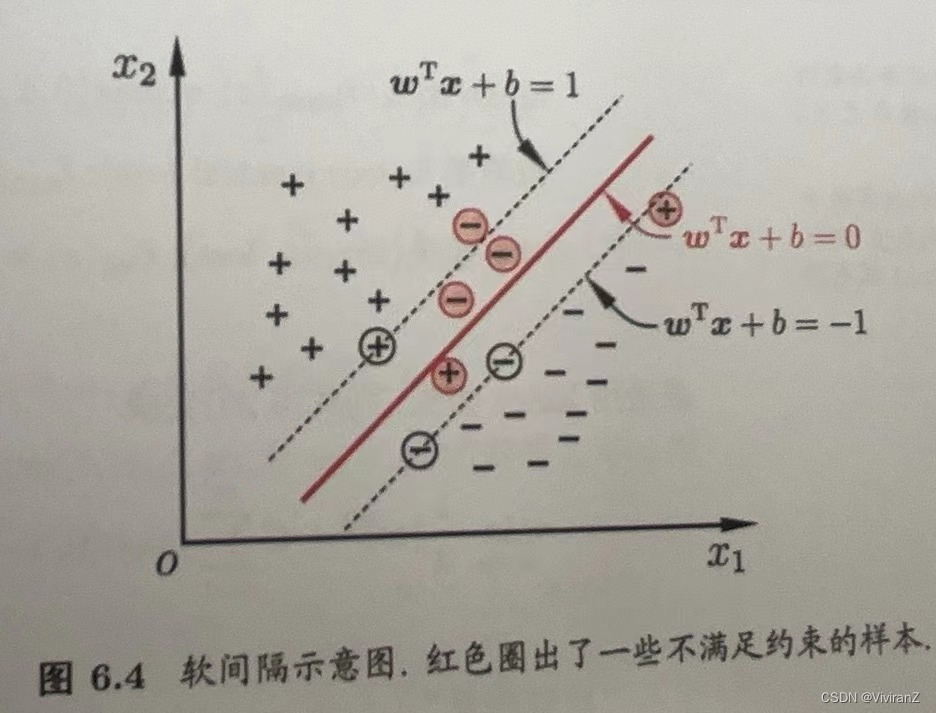
那么问题就变成如何让不满足约束的样本尽量少。 

线性SVM之硬间隔和软间隔的直觉和原理 - 知乎

这个讲得还挺清晰的。。。 ​​​​​​​

 

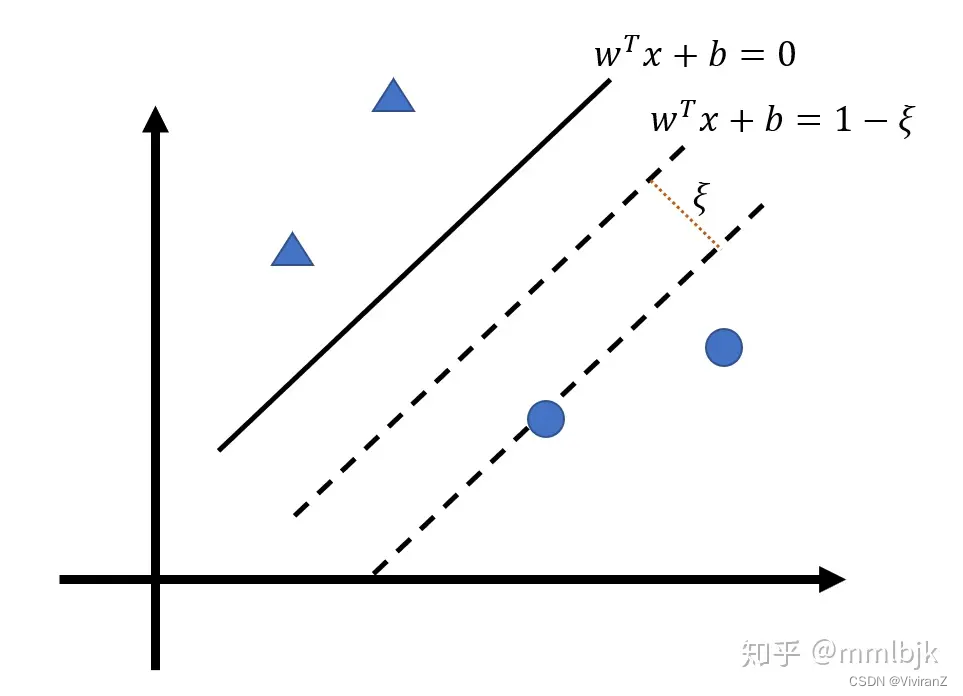
三、支持向量回归

回归问题和分类问题不同，分类是希望样本尽量远离预测的超平面，而回归是希望样本尽量靠近预测的超平面。一般来说就是落入间隔带。 

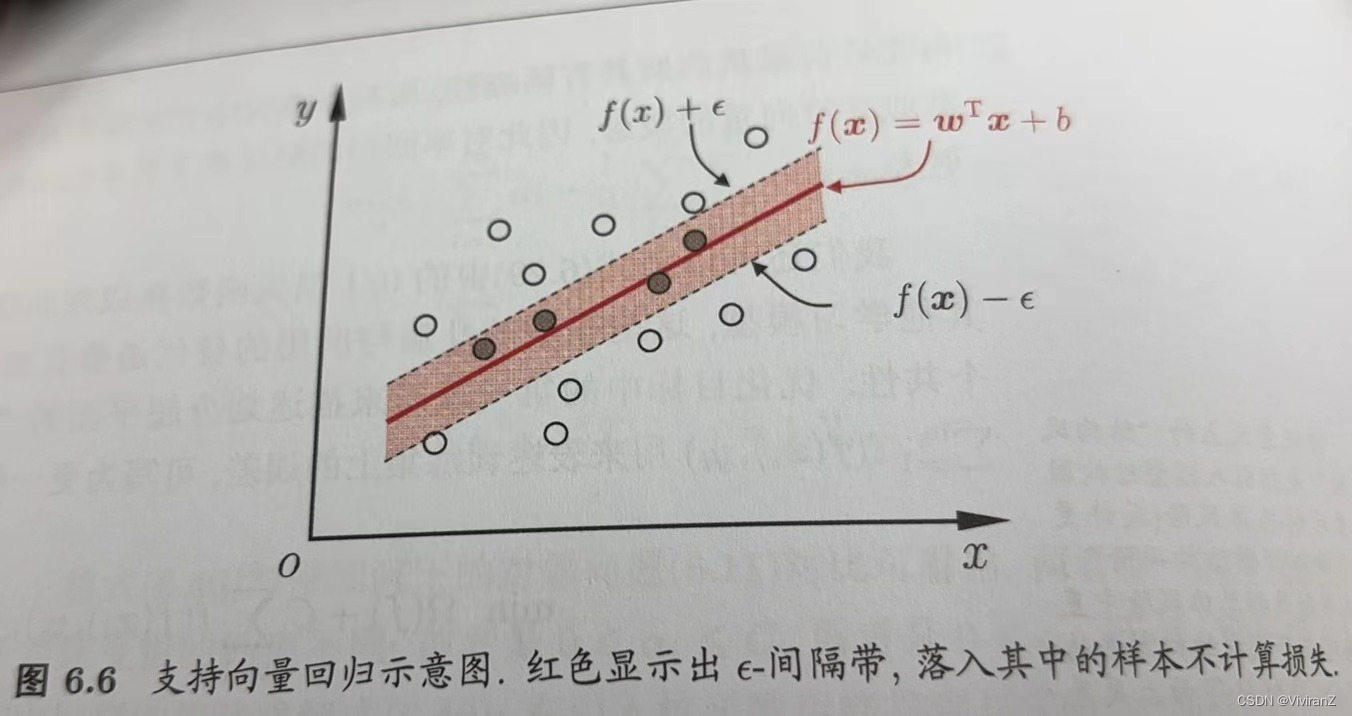
细节不表。可参考西瓜书。

参考文献：

[1] https://en.wikipedia.org/wiki/Support_vector_machine

[2]《机器学习》周志华

[3]支持向量机（SVM）——原理篇

[4]浅入浅出核方法 (Kernel Method) - 知乎 

[5] 线性SVM之硬间隔和软间隔的直觉和原理 - 知乎