目录

一、引言

二、梯度下降算法的原理

 三、梯度下降算法的实现

四、梯度下降算法的优缺点

优点：

缺点：

五、梯度下降算法的改进策略

1 随机梯度下降（Stochastic Gradient Descent, SGD）

2 批量梯度下降（Batch Gradient Descent)

3 小批量梯度下降（Mini-batch Gradient Descent）

4 动量法（Momentum）

5 Adam算法

六、总结

---

一、引言

梯度下降算法是机器学习领域中最常用的优化算法之一。无论是线性回归、逻辑回归、神经网络还是深度学习，我们都可以看到梯度下降的身影。它之所以如此受欢迎，是因为其原理简单、易于实现，并且在许多情况下都能得到不错的效果。本文将详细介绍梯度下降算法的原理、实现方法、优缺点以及改进策略。

二、梯度下降算法的原理

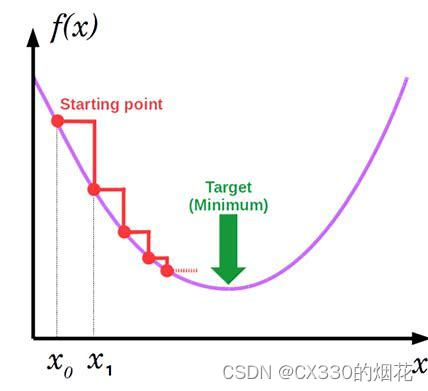
梯度下降算法的基本思想是利用目标函数的梯度信息来指导参数的更新，从而逐步逼近函数的最小值点。假设我们要优化的目标函数为f(x)，其中x是一个n维向量，表示模型的参数。我们的目标是找到x的最优值，使得f(x)取得最小值。

梯度下降算法的工作流程如下：

1. 初始化参数x，可以随机初始化或者根据经验设置。
2. 计算目标函数f(x)在当前位置x的梯度∇f(x)。梯度是一个向量，表示函数在各个方向上的变化率。在梯度下降算法中，我们利用梯度的负方向（即-∇f(x)）作为参数更新的方向。
3. 按照一定的步长α（也称为学习率）沿着梯度的负方向更新参数，即x = x - α∇f(x)。步长α是一个超参数，需要根据实际情况进行调整。步长过大可能导致算法发散，步长过小则可能导致收敛速度过慢。
4. 重复步骤2和3直到满足停止条件（如达到预设的迭代次数、目标函数的值变化小于某个阈值等）。

 三、梯度下降算法的实现

梯度下降算法的实现相对简单，下面是一个基本的Python实现示例：

import numpy as np

def gradient_descent(f, grad_f, x_start, alpha, num_iters):
    """
    f: 目标函数
    grad_f: 目标函数的梯度函数
    x_start: 参数的初始值
    alpha: 学习率
    num_iters: 迭代次数
    """
    x = x_start
    for i in range(num_iters):
        grad = grad_f(x)
        x = x - alpha * grad
    return x

在这个示例中，我们假设目标函数f和它的梯度函数grad_f都是已知的。通过不断迭代更新参数x，最终得到最优解。

四、梯度下降算法的优缺点

优点：

1. 原理简单，易于实现。在许多情况下都能得到不错的效果。
2. 可以应用于各种规模的数据集。

缺点：

1. 对于非凸函数，可能陷入局部最优解而不是全局最优解。
2. 收敛速度较慢，尤其是在处理大规模数据集时。
3. 需要选择合适的步长α，不同的步长可能导致不同的结果。
4. 对于特征之间存在相关性的情况，梯度下降算法可能会变得非常慢。

五、梯度下降算法的改进策略

为了解决梯度下降算法存在的问题，人们提出了许多改进策略，下面介绍几种常见的改进方法：

1 随机梯度下降（Stochastic Gradient Descent, SGD）

SGD在每次迭代时只使用一个样本来计算梯度并更新参数。这样可以减少计算量并提高收敛速度，但也可能导致参数更新的方向不稳定。

2 批量梯度下降（Batch Gradient Descent)

批量梯度下降在每次迭代时使用所有样本来计算梯度并更新参数。这种方法可以得到更准确的梯度估计但计算量较大。

3 小批量梯度下降（Mini-batch Gradient Descent）

小批量梯度下降是批量梯度下降和随机梯度下降的一种折中方法。它每次迭代时使用一部分样本来计算梯度并更新参数，既减少了计算量又保持了参数更新的稳定性。

4 动量法（Momentum）

动量法通过引入一个动量项来加速SGD的收敛速度。在每次迭代时，动量项会保留一部分上一次迭代的更新方向，并与当前梯度相结合来更新参数。这样可以减少震荡并加速收敛。

5 Adam算法

Adam算法是一种结合了Momentum和RMSProp的优化算法。它通过计算梯度的一阶矩（平均值）和二阶矩（未中心化的方差）来动态调整每个参数的学习率。Adam算法在许多情况下都能取得很好的效果，并且对于超参数的调整相对鲁棒。

六、总结

梯度下降算法作为一种经典的优化算法，在机器学习和人工智能领域有着广泛的应用。虽然它存在一些缺点，但通过不断改进和优化，我们可以克服这些问题并提高算法的性能。

未来随着深度学习和其他复杂模型的不断发展，梯度下降算法及其改进策略将继续发挥重要作用。