文心一言 VS 讯飞星火 VS chatgpt （206）-- 算法导论15.4 3题

news2024/9/29 17:37:09

三、设计 LCS-LENGTH的带备忘的版本，运行时间为O(mn)。需要写代码的时候，请用go语言。

文心一言，代码正常运行：

LCS-LENGTH（Longest Common Subsequence Length）问题的带备忘的版本通常指的是使用动态规划（Dynamic Programming, DP）和备忘录（Memoization）来优化算法性能，避免重复计算。通过维护一个表（即“备忘录”）来存储已经计算过的子问题的解，从而在解决新问题时可以直接查找已存储的结果，而不是重新计算。

以下是使用Go语言实现的一个带备忘的LCS-LENGTH算法的示例。在这个示例中，lcsLength 函数计算两个字符串的最长公共子序列长度，并且使用一个二维数组 memo 来存储子问题的解，其中 memo[i][j] 存储的是 str1 的前 i 个字符和 str2 的前 j 个字符的最长公共子序列长度。

package main  
  
import (  
	"fmt"  
)  
  
func lcsLength(str1, str2 string) int {  
	m, n := len(str1), len(str2)  
	memo := make([][]int, m+1)  
	for i := range memo {  
		memo[i] = make([]int, n+1)  
	}  
  
	for i := 1; i <= m; i++ {  
		for j := 1; j <= n; j++ {  
			if str1[i-1] == str2[j-1] {  
				memo[i][j] = memo[i-1][j-1] + 1  
			} else {  
				memo[i][j] = max(memo[i-1][j], memo[i][j-1])  
			}  
		}  
	}  
  
	return memo[m][n]  
}  
  
func max(a, b int) int {  
	if a > b {  
		return a  
	}  
	return b  
}  
  
func main() {  
	str1 := "ABCDEFG"  
	str2 := "XYZABCDEFGHIJKL"  
	length := lcsLength(str1, str2)  
	fmt.Printf("The length of the Longest Common Subsequence is: %d\n", length)  
}

在这个实现中，lcsLength 函数首先初始化一个 (m+1) x (n+1) 的二维数组 memo，其中 m 和 n 分别是两个输入字符串 str1 和 str2 的长度。然后，它使用两个嵌套的循环来遍历 str1 和 str2 的所有字符组合。

如果 str1 的第 i 个字符和 str2 的第 j 个字符相同，则最长公共子序列的长度加一，即 memo[i][j] = memo[i-1][j-1] + 1。如果不同，则最长公共子序列的长度是去掉 str1 的第 i 个字符后的最长公共子序列和去掉 str2 的第 j 个字符后的最长公共子序列中的较大值，即 memo[i][j] = max(memo[i-1][j], memo[i][j-1])。

最后，函数返回 memo[m][n]，即两个字符串的最长公共子序列的长度。

请注意，这个实现的时间复杂度是 O(mn)，其中 m 和 n 分别是两个输入字符串的长度。这是因为我们需要填充一个 m x n 的表，而每个表项的计算时间是常数时间。

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

讯飞星火，代码正常运行：

在Go语言中，我们可以使用动态规划来解决这个问题。以下是实现LCS-LENGTH的带备忘的版本的代码：

package main
import "fmt"

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

func lcsLength(X, Y []int) int {
    m := len(X)
    n := len(Y)
    c := make([][]int, m+1)
    for i := range c {
        c[i] = make([]int, n+1)
    }
    for i := 0; i <= m; i++ {
        for j := 0; j <= n; j++ {
            if i == 0 || j == 0 {
                c[i][j] = 0
            } else if X[i-1] == Y[j-1] {
                c[i][j] = c[i-1][j-1] + 1
            } else {
                c[i][j] = max(c[i-1][j], c[i][j-1])
            }
        }
    }
    return c[m][n]
}

func main() {
    X := []int{1, 3, 4, 5, 6, 7, 7, 8}
    Y := []int{2, 3, 5, 6, 7, 8, 9, 10}
    fmt.Println("Length of LCS is", lcsLength(X, Y))
}

在这个程序中，我们首先定义了一个二维数组c，用于存储子问题的解。然后，我们遍历两个输入序列，如果当前位置的元素相同，则该位置的LCS长度为左上角元素的LCS长度加一；否则，该位置的LCS长度为左边元素和上边元素中较大的那个LCS长度。最后，右下角的元素就是整个序列的LCS长度。

在这里插入图片描述

在这里插入图片描述

360智脑，代码不能运行：

以下是一个使用Go语言实现的LCS-Length带备忘的版本：

package main

func lcsLength(memo map[int][int]int, X string, Y string, m int, n int) int {
    if m == 0 || n == 0 {
        return 0
    }

    if v, ok := memo[m][n]; ok {
        return v
    }

    if X[m-1] == Y[n-1] {
        memo[m][n] = lcsLength(memo, X, Y, m-1, n-1) + 1
    } else {
        memo[m][n] = max(lcsLength(memo, X, Y, m-1, n), lcsLength(memo, X, Y, m, n-1))
    }

    return memo[m][n]
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

func main() {
    X := "ABCBDAB"
    Y := "BDCAB"
    memo := make(map[int][int]int)
    m := len(X)
    n := len(Y)
    fmt.Println(lcsLength(memo, X, Y, m, n))
}

在这个代码中，我们使用了一个备忘录（memo）来存储之前计算过的LCS长度。当我们计算LCS长度时，我们首先检查备忘录中是否已经有这个值。如果有，我们就直接返回它；如果没有，我们就计算它，并将其存储在备忘录中。

这个算法的运行时间为O(mn)，因为我们在计算LCS长度时，最多需要遍历X和Y字符串的每个字符。

在这里插入图片描述

在这里插入图片描述

智谱清言，代码正常运行：

为了设计一个运行时间为O(mn)的LCS-LENGTH算法，我们可以使用动态规划(DP)技术，并辅以带备忘的递归方法来避免重复计算。在下面给出的Go语言代码中，我们将计算两个字符串str1和str2的最长公共子序列的长度。

package main
import (
	"fmt"
)
// LCSLength 计算两个字符串的最长公共子序列的长度
// 使用带备忘的递归方法
func LCSLength(str1, str2 string) int {
	// 创建一个二维切片来保存子问题的结果
	// dp[i][j] 表示str1的前i个字符与str2的前j个字符的LCS长度
	dp := make([][]int, len(str1)+1)
	for i := range dp {
		dp[i] = make([]int, len(str2)+1)
	}
	// 初始化dp数组
	for i := 0; i <= len(str1); i++ {
		for j := 0; j <= len(str2); j++ {
			if i == 0 || j == 0 {
				dp[i][j] = 0
			}
		}
	}
	// 递归计算LCS长度，同时更新dp数组
	return recursiveLCSLength(str1, str2, 0, 0, dp)
}
// recursiveLCSLength 递归计算最长公共子序列的长度
// 同时更新dp数组以避免重复计算
func recursiveLCSLength(str1, str2 string, i, j int, dp [][]int) int {
	// 检查是否已经计算过这个子问题
	if dp[i][j] != 0 {
		return dp[i][j]
	}
	// 如果i或j为0，那么LCS长度为0
	if i == 0 || j == 0 {
		dp[i][j] = 0
		return 0
	}
	// 如果str1[i-1] == str2[j-1]，那么当前字符是LCS的一部分
	if str1[i-1] == str2[j-1] {
		dp[i][j] = 1 + recursiveLCSLength(str1, str2, i-1, j-1, dp)
	} else {
		// 否则，取左侧或上侧的LCS长度中的较大值
		dp[i][j] = max(recursiveLCSLength(str1, str2, i-1, j, dp), recursiveLCSLength(str1, str2, i, j-1, dp))
	}
	return dp[i][j]
}
// max 返回两个整数中的较大值
func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}
func main() {
	str1 := "ABCBDAB"
	str2 := "BDCAB"
	fmt.Println("The length of LCS is:", LCSLength(str1, str2))
}

这段代码定义了一个LCSLength函数，它使用一个二维切片dp来存储子问题的解，并且通过递归函数recursiveLCSLength来计算最长公共子序列的长度。递归函数会在每次需要计算相同子问题时，检查是否已经在dp中存储了结果，以避免重复计算。

main函数中给出了一个例子，计算字符串"ABCBDAB"和"BDCAB"的最长公共子序列的长度，并打印结果。

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

天工，代码正常运行：

Certainly! Below is an implementation of the LCS problem with memoization in Go that runs in O(mn) time, where m and n are the lengths of the two input strings. This implementation uses a二维数组 to store the results of subproblems, avoiding重复计算.

package main

import "fmt"

// LCSMemo computes the length of the longest common subsequence between X and Y using memoization.
func LCSMemo(X, Y string) int {
	m, n := len(X), len(Y)
	dp := make([][]int, m+1)
	for i := range dp {
		dp[i] = make([]int, n+1)
	}

	for i := 1; i <= m; i++ {
		for j := 1; j <= n; j++ {
			if X[i-1] == Y[j-1] {
				dp[i][j] = dp[i-1][j-1] + 1
			} else {
				dp[i][j] = max(dp[i-1][j], dp[i][j-1])
			}
		}
	}

	return dp[m][n]
}

// max returns the larger of two integers.
func max(a, b int) int {
	if a >= b {
		return a
	}
	return b
}

func main() {
	X := "AGGTAB"
	Y := "GXTXAYB"
	length := LCSMemo(X, Y)
	fmt.Printf("Length of LCS: %d\n", length)
}

To use this code, simply run it with the Go runtime and it will output the length of the longest common subsequence between the two given strings. The max function is used to handle the comparison of integers, as int in Go does not guarantee a specific signedness.

在这里插入图片描述

在这里插入图片描述

灵小智，代码正常运行：

下面是用Go语言编写的带备忘录的最长公共子序列（LCS）问题的代码示例：

package main

import (
	"fmt"
)

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

func lcsLengthMemoized(X, Y string, m, n int, memo [][]int) int {
	if m == 0 || n == 0 {
		return 0
	}

	if memo[m][n] != -1 {
		return memo[m][n]
	}

	if X[m-1] == Y[n-1] {
		memo[m][n] = 1 + lcsLengthMemoized(X, Y, m-1, n-1, memo)
		return memo[m][n]
	}

	memo[m][n] = max(lcsLengthMemoized(X, Y, m-1, n, memo), lcsLengthMemoized(X, Y, m, n-1, memo))
	return memo[m][n]
}

func lcsLength(X, Y string) int {
	m := len(X)
	n := len(Y)

	memo := make([][]int, m+1)
	for i := range memo {
		memo[i] = make([]int, n+1)
		for j := range memo[i] {
			memo[i][j] = -1
		}
	}

	return lcsLengthMemoized(X, Y, m, n, memo)
}

func main() {
	X := "ABCBDAB"
	Y := "BDCAB"

	fmt.Printf("Length of LCS: %d\n", lcsLength(X, Y))
}

在这个代码中，我们使用了备忘录（memo）来保存已计算过的子问题的结果，以避免重复计算。通过将已计算过的结果存储在备忘录中，我们可以将算法的运行时间从指数级别降低到线性级别。这样，算法的运行时间为O(mn)，其中m和n分别是字符串X和Y的长度。

以上是用Go语言编写的带备忘录的LCS问题的代码示例，希望对你有帮助！

在这里插入图片描述

在这里插入图片描述

chatgpt，代码正常运行：

当设计LCS-LENGTH函数的带备忘的版本时，可以使用动态规划的思想。下面是用Go语言实现的代码：

package main

import (
	"fmt"
)

func lcsLengthMemo(X, Y string) int {
	m := len(X)
	n := len(Y)

	// 创建并初始化备忘录
	memo := make([][]int, m+1)
	for i := 0; i <= m; i++ {
		memo[i] = make([]int, n+1)
		for j := 0; j <= n; j++ {
			memo[i][j] = -1
		}
	}

	var lcs func(int, int) int
	lcs = func(i, j int) int {
		if memo[i][j] != -1 { // 如果已经计算过，直接返回备忘录中的值
			return memo[i][j]
		}
		
		if i == 0 || j == 0 { // 边界条件，其中一个字符串为空
			memo[i][j] = 0
			return 0
		}

		if X[i-1] == Y[j-1] { // 当前字符匹配成功，继续向前匹配
			memo[i][j] = lcs(i-1, j-1) + 1
			return memo[i][j]
		} else { // 当前字符不匹配，取两种情况下的最大值
			left := lcs(i-1, j)
			top := lcs(i, j-1)
			if left > top {
				memo[i][j] = left
			} else {
				memo[i][j] = top
			}
			return memo[i][j]
		}
	}

	return lcs(m, n)
}

func main() {
	X := "ABCBDAB"
	Y := "BDCAB"
	fmt.Println("LCS长度:", lcsLengthMemo(X, Y))
}

该代码使用了备忘录来存储已经计算过的子问题的结果，避免重复计算。通过递归方式进行动态规划，从后往前匹配字符串，并记录最长公共子序列的长度。运行时间复杂度为O(mn)。

在这里插入图片描述

在这里插入图片描述

kimi，代码正常运行：

在 Go 语言中，设计一个带有备忘（Memoization）的 LCS-LENGTH 版本，可以通过创建一个额外的二维切片来存储已经计算过的子问题的解。这样，当我们需要计算一个新的子问题时，我们首先检查这个解是否已经被计算过。如果已经计算过，我们可以直接使用这个解，而不需要重新计算，从而提高算法的效率。

以下是带有备忘的 LCS-LENGTH 函数的 Go 语言实现：

package main

import (
	"fmt"
)

// LCS-LENGTH 函数计算两个序列的最长公共子序列的长度
func LCSLength(x, y []int) int {
	m, n := len(x), len(y)
	memo := make([][]int, m+1)
	for i := range memo {
		memo[i] = make([]int, n+1)
	}

	return lcsLengthMemo(x, y, m, n, memo)
}

// lcsLengthMemo 是 LCS-LENGTH 的递归实现，带有备忘
func lcsLengthMemo(x, y []int, m, n int, memo [][]int) int {
	if m == 0 || n == 0 {
		return 0
	}

	// 检查解是否已经在备忘数组中
	if memo[m][n] != 0 {
		return memo[m][n]
	}

	if x[m-1] == y[n-1] {
		// 如果当前元素相同，递归计算去掉这两个元素后的子问题的解
		memo[m][n] = 1 + lcsLengthMemo(x, y, m-1, n-1, memo)
	} else {
		// 如果当前元素不同，分别计算两种情况的解，并取最大值
		memo[m][n] = max(
			lcsLengthMemo(x, y, m-1, n, memo),
			lcsLengthMemo(x, y, m, n-1, memo),
		)
	}

	return memo[m][n]
}

// max 返回两个整数中的最大值
func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

func main() {
	x := []int{1, 0, 0, 1, 0, 1, 0, 1}
	y := []int{0, 1, 0, 1, 1, 0, 1, 1, 0}

	length := LCSLength(x, y)
	fmt.Printf("Length of LCS: %d\n", length)
}

在这个实现中，LCSLength 函数是用户调用的接口，它初始化备忘数组并调用 lcsLengthMemo 函数。lcsLengthMemo 函数是递归实现，它使用备忘数组来避免重复计算。这个算法的时间复杂度是 O(m * n)，因为每个子问题只计算一次，并且我们使用 O(m * n) 的空间来存储备忘数组。

在这里插入图片描述

在这里插入图片描述

混元，代码正常运行：

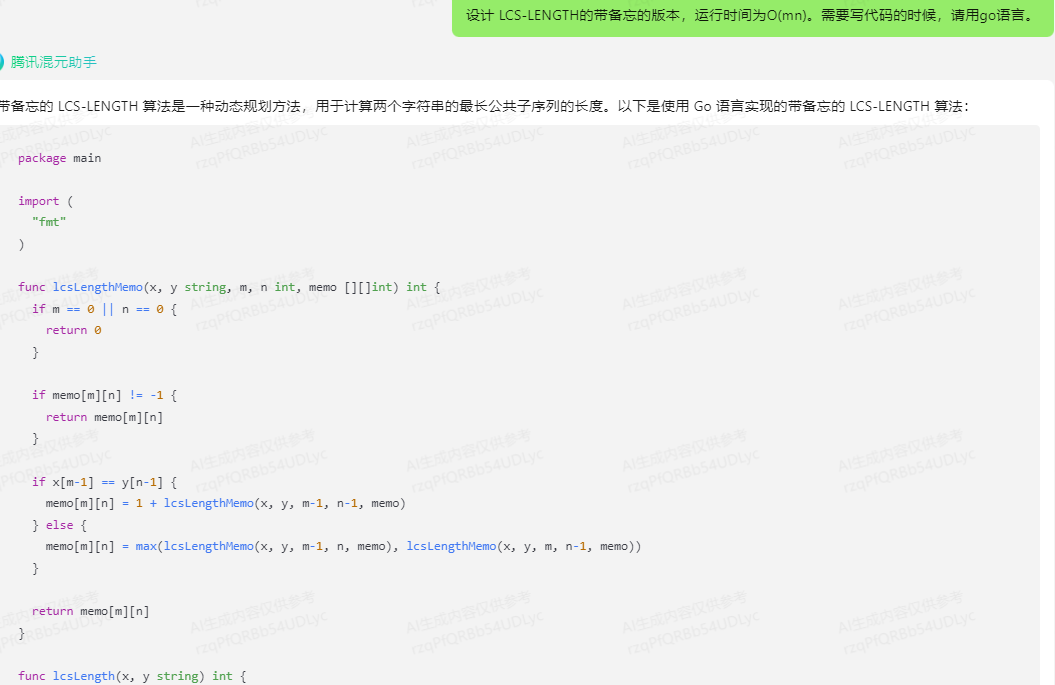
带备忘的 LCS-LENGTH 算法是一种动态规划方法，用于计算两个字符串的最长公共子序列的长度。以下是使用 Go 语言实现的带备忘的 LCS-LENGTH 算法：

package main

import (
	"fmt"
)

func lcsLengthMemo(x, y string, m, n int, memo [][]int) int {
	if m == 0 || n == 0 {
		return 0
	}

	if memo[m][n] != -1 {
		return memo[m][n]
	}

	if x[m-1] == y[n-1] {
		memo[m][n] = 1 + lcsLengthMemo(x, y, m-1, n-1, memo)
	} else {
		memo[m][n] = max(lcsLengthMemo(x, y, m-1, n, memo), lcsLengthMemo(x, y, m, n-1, memo))
	}

	return memo[m][n]
}

func lcsLength(x, y string) int {
	m, n := len(x), len(y)
	memo := make([][]int, m+1)
	for i := range memo {
		memo[i] = make([]int, n+1)
		for j := range memo[i] {
			memo[i][j] = -1
		}
	}

	return lcsLengthMemo(x, y, m, n, memo)
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

func main() {
	x := "ABCBDAB"
	y := "BDCAB"
	fmt.Printf("The length of the LCS is: %d\n", lcsLength(x, y))
}

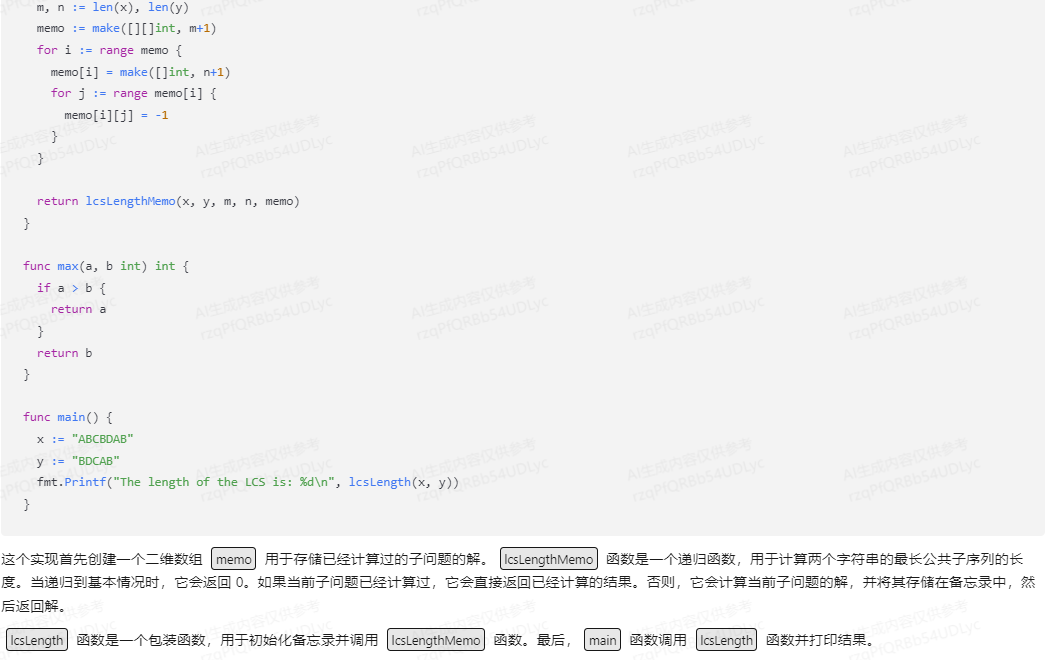
这个实现首先创建一个二维数组 memo 用于存储已经计算过的子问题的解。lcsLengthMemo 函数是一个递归函数，用于计算两个字符串的最长公共子序列的长度。当递归到基本情况时，它会返回 0。如果当前子问题已经计算过，它会直接返回已经计算的结果。否则，它会计算当前子问题的解，并将其存储在备忘录中，然后返回解。

lcsLength 函数是一个包装函数，用于初始化备忘录并调用 lcsLengthMemo 函数。最后，main 函数调用 lcsLength 函数并打印结果。

在这里插入图片描述

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1485509.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

备考2024年小学生古诗文大会：历年真题15题练习和独家解析

备考2024年小学生古诗文大会：历年真题15题练习和独家解析

如何提高小学生古诗词的知识&#xff1f;如何激发小学生古诗词的学习兴趣&#xff1f;如何提高小学古诗词的学习成绩&#xff1f;如何备考2024年小学生古诗文大会&#xff1f;... 如果你也在关注这些问题&#xff0c;我的建议是参加每年一度的小学生古诗词大会&#xff08;免费…
阅读更多...
金融行业专题｜期货超融合架构转型与场景探索合集（2023版）

金融行业专题｜期货超融合架构转型与场景探索合集（2023版）

更新内容&#xff1a; 更新 SmartX 超融合在期货行业的覆盖范围、部署规模与应用场景。新增 CTP 主席系统实践与评测、容器云资源池等场景实践。更多超融合金融核心生产业务场景实践&#xff0c;欢迎下载阅读电子书《SmartX 金融核心生产业务场景探索文章合集》。 面对不断变…
阅读更多...
云计算与大数据课程笔记（一）云计算背景与介绍

云计算与大数据课程笔记（一）云计算背景与介绍

如何实现一个简易搜索引擎&#xff1f; 实现一个简易的搜索引擎可以分为几个基本步骤&#xff1a;数据收集&#xff08;爬虫&#xff09;、数据处理&#xff08;索引&#xff09;、查询处理和结果呈现。下面是一个概括的实现流程&#xff1a; 1. 数据收集&#xff08;爬虫&am…
阅读更多...
Android和Linux的嵌入式开发差异

Android和Linux的嵌入式开发差异

最近开始投入Android的怀抱。说来惭愧&#xff0c;08年就听说这东西&#xff0c;当时也有同事投入去看&#xff0c;因为恶心Java&#xff0c;始终对这玩意无感&#xff0c;没想到现在不会这个嵌入式都快要没法搞了。为了不中年失业&#xff0c;所以只能回过头又来学。 首先还是…
阅读更多...
vue实现水印功能

vue实现水印功能

目录 一、应用场景 二、实现原理 三、详细开发 1.水印的实现方式 2.防止用户通过控制台修改样式去除水印效果&#xff08;可跳过&#xff0c;有弊端&#xff09; 3.水印的使用 &#xff08;1&#xff09;单页面/全局使用 &#xff08;2&#xff09;全局使用个别页面去掉…
阅读更多...
MySQL 常用优化方式

MySQL 常用优化方式

MySQL 常用优化方式 sql 书写顺序与执行顺序SQL设计优化使用索引避免索引失效分析慢查询合理使用子查询和临时表列相关使用 日常SQL优化场景limit语句隐式类型转换嵌套子查询混合排序查询重写 sql 书写顺序与执行顺序 (7) SELECT (8) DISTINCT <select_list> (1) FROM &…
阅读更多...
18.题目：编号760 数的计算

18.题目：编号760 数的计算

题目&#xff1a; ###该题主要考察递推、递归 将该题看成若干个子问题 #include<bits/stdc.h> using namespace std; const int N20; int a[N];int dfs(int dep){int res1;for(int i1;i<a[dep-1]/2;i){a[dep]i;resdfs(dep1);}return res; }int main(){int n;cin>…
阅读更多...
论文阅读_代码生成模型_CodeLlama

论文阅读_代码生成模型_CodeLlama

英文名称: Code Llama: Open Foundation Models for Code 中文名称: Code Llama&#xff1a;开放基础代码模型 链接: https://arxiv.org/abs/2308.12950 代码: https://github.com/facebookresearch/codellama 作者: Baptiste Rozire, Jonas Gehring, Fabian Gloeckle, Sten So…
阅读更多...
React的fiber原理

React的fiber原理

在读完这篇文章之后&#xff0c;大家可以回到文章开头再捋一下以下几个关键词&#xff0c;将React的 Fiber架构原理彻底搞清楚。 关键词&#xff1a; requestIdleCallback、IdleDeadlineFiber&#xff1a;React的一个执行单元 在Fiber 出现之前&#xff0c;React存在什么问题…
阅读更多...
bxCAN总线Loopback功能实现（STM32F4xx）

bxCAN总线Loopback功能实现（STM32F4xx）

目录 概述 1 认识bxCAN Loopback 1.1 环回模式 1.2 环回模式特点 2 使用STM32CubeMX 生成工程 2.1 参数配置 2.2 生成工程代码 2.4 了解can.c 3 认识Hal库中的bxCAN 3.1 认识3个重要数据结构 3.2 函数组 3.2.1 初始化函数组 3.2.2 控制函数组 3.2.3 中断管理函数…
阅读更多...
【风格迁移】pix2pixHD：高分辨率图像生成

【风格迁移】pix2pixHD：高分辨率图像生成

pix2pixHD&#xff1a;高分辨率图像生成 提出背景问题1: 如何提高生成图像的照片级真实感和分辨率&#xff1f;问题2: 如何利用实例级别的对象语义信息进一步提高图像质量&#xff1f;问题3: 如何实现图像合成的多模态性&#xff0c;允许交互式对象编辑&#xff1f; pix2pixHD …
阅读更多...
【STK】手把手教你利用STK进行仿真-STK软件基础01 STK的对象组织模式

【STK】手把手教你利用STK进行仿真-STK软件基础01 STK的对象组织模式

STK系统采用面向对象和分级组织结构的管理模式对仿真对象进行管理&#xff0c;这种组织二行管理模式非常符合人类的认知习惯&#xff0c;易于理解。STK最基本的对象为场景&#xff08;Scenario&#xff09;&#xff0c;在场景中可以面向对象和分级组织模式对各场景中的仿真对象…
阅读更多...
[c++] c++ 中的顺序(构造，析构，初始化列表，继承)

[c++] c++ 中的顺序(构造，析构，初始化列表，继承)

对象构造的时候&#xff0c;对象成员变量的初始化顺序是什么样的 &#xff1f; 派生类构造的时候&#xff0c;先构造基类还是先构造派生类 &#xff1f; 构造函数中的初始化列表&#xff0c;初始化的顺序是列表的顺序吗 &#xff1f; 析构的时候&#xff0c;析构的顺序是什么…
阅读更多...
华为数通方向HCIP-DataCom H12-821题库(多选题：41-60)

华为数通方向HCIP-DataCom H12-821题库(多选题：41-60)

第41题 BGP OPEN消息中携带如下哪些信息? A、路由属性 B、BGP Router ID C、Hold time D、本地自治系统(AS)号 【参考答案】BCD 【答案解析】 B. BGP Router ID：OPEN消息中包含发送方BGP路由器的Router ID，用于唯一标识BGP路由器。C.Hold time：OPEN消息中包含发送方BGP路由…
阅读更多...
区块链媒体发布推广10个热门案例解析-华媒舍

区块链媒体发布推广10个热门案例解析-华媒舍

区块链技术的发展已经引起了媒体的广泛关注&#xff0c;越来越多的区块链媒体纷纷发布推广相关的热门案例。本文将介绍10个成功的区块链媒体推广案例&#xff0c;并分享它们的成功秘诀&#xff0c;帮助读者更好地了解区块链媒体推广的方法与技巧。 随着区块链技术的成熟和应用场…
阅读更多...
vue2本地开发环境正常，生产环境下this.$router.push({ name: ‘login‘ })不跳转

vue2本地开发环境正常，生产环境下this.$router.push({ name: ‘login‘ })不跳转

如果在Vue.js 2中在本地开发环境下正常运行，但在生产环境下使用​​this.$router.push({ name: login })​​不起作用，可能有几个原因需要检查和解决： 路由配置问题： 确保你的路由配置正确，特别是确保在生产环境中，路由的配置和本地开发环境一致。检查是否正确设置了name…
阅读更多...
课程表系列(BFS)

课程表系列(BFS)

广度优先搜索 文章目录 广度优先搜索207. 课程表210. 课程表 II思路 630. 课程表 III1462. 课程表 IV547. 省份数量 207. 课程表 207. 课程表 你这个学期必须选修 numCourses 门课程&#xff0c;记为 0 到 numCourses - 1 。 在选修某些课程之前需要一些先修课程。 先修课程…
阅读更多...
多元函数积分思路合集

多元函数积分思路合集

[曲线积分笔记]第一类曲线积分 [微积分笔记]第二类曲线/面积分总结 积分方法意义/提示平面第二型曲线积分化为定积分 ∮ L → ∫ a b \oint_L \to \int_a^b ∮L​→∫ab​平面第二型曲线积分格林公式 ∮ L → ∬ D \oint_L \to \iint_D ∮L​→∬D​化为对平面区域的二重积分空…
阅读更多...
百度搜索引擎SEO优化方法

百度搜索引擎SEO优化方法

随着互联网的不断发展&#xff0c;搜索引擎已经成为人们获取信息、产品和服务的主要途径之一。而在中国&#xff0c;百度作为最大的搜索引擎&#xff0c;其影响力不可忽视。了解并掌握百度SEO关键词优化方法&#xff0c;对于提升网站在搜索引擎中的排名至关重要。 关键词选择&a…
阅读更多...
chatgpt-3的文章生成器有哪些？可以批量生成文章的生成器

chatgpt-3的文章生成器有哪些？可以批量生成文章的生成器

GPT-3&#xff08;Generative Pre-trained Transformer 3&#xff09;作为人工智能领域的一项重大突破&#xff0c;开启了新一代的文本生成技术。同时市面上也涌现出了一些GPT-3文章生成器&#xff0c;为用户提供了快速、高效地生成各种类型文章的工具。本文将介绍一些中国的GP…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023