课程表系列(BFS)

广度优先搜索

文章目录

广度优先搜索
- 207. 课程表
- 210. 课程表 II
- - 思路
- 630. 课程表 III
- 1462. 课程表 IV
- 547. 省份数量

207. 课程表

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则必须先学习课程 bi 。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。

示例 2：

输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

class Solution {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        List<List<Integer>> list=new ArrayList<List<Integer>>();//邻接表存图
        for(int i=0;i<numCourses;i++)
            list.add(new ArrayList<>());
        int[] indeg=new int[numCourses];//入度数组,下标对应结点
        for(int i=0;i<prerequisites.length;i++)
        {
            list.get(prerequisites[i][0]).add(prerequisites[i][1]);//创建邻接表
            indeg[prerequisites[i][1]]++;//入度+1
        }
        Queue<Integer> queue=new LinkedList<>();//遍历时,用于存每个结点的队列,这里的结点形式是在邻接表中对应的下标
        //寻找入度为0的结点，当作起点加入队列中
        for(int i=0;i<numCourses;i++)
        {
            if(indeg[i]==0)
                queue.add(i);
        }
        //bfs部分
        while(!queue.isEmpty())
        {
            //将出度为0的结点全部出队
            for(int i=queue.size();i>0;i--)
            {
                //获取结点的下标,并出队
                Integer node=queue.poll();
                //遍历该结点到达了哪些结点,并将那些结点入度-1;
                for(Integer j:list.get(node))
                {
                    indeg[j]--;
                    //可以学习该课程了，入队
                    if(indeg[j]==0)
                    {
                        queue.add(j);
                    }
                }
            }
        }
        //最后判断入度数组是否全为0
        for(int i=0;i<numCourses;i++)
        {
            if(indeg[i]!=0)return false;
        }
        return true;

    }
}

210. 课程表 II

现在你总共有 numCourses 门课需要选，记为 0 到 numCourses - 1。给你一个数组 prerequisites ，其中 prerequisites[i] = [ai, bi] ，表示在选修课程 ai 前必须先选修 bi 。

例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示：[0,1] 。

返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序，你只要返回 任意一种 就可以了。如果不可能完成所有课程，返回 一个空数组 。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]]
输出：[0,1]
解释：总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1] 。

思路

本题与课程表1很相似，唯一区别：只是改了学习箭头反过来了，然后在层序遍历的同时将遍历的结点存起来

class Solution {
    public int[] findOrder(int numCourses, int[][] prerequisites) {
        List<List<Integer>> list=new ArrayList<List<Integer>>();//邻接表存图
        int[] res=new int[numCourses];//学习课程顺序
        for(int i=0;i<numCourses;i++)
            list.add(new ArrayList<>());
        int[] indeg=new int[numCourses];//入度数组,下标对应结点
        for(int i=0;i<prerequisites.length;i++)
        {
            list.get(prerequisites[i][1]).add(prerequisites[i][0]);//创建邻接表
            indeg[prerequisites[i][0]]++;//入度+1
        }
        Queue<Integer> queue=new LinkedList<>();//遍历时,用于存每个结点的队列,这里的结点形式是在邻接表中对应的下标
        //寻找入度为0的结点，当作起点加入队列中
        for(int i=0;i<numCourses;i++)
        {
            if(indeg[i]==0)
                queue.add(i);
        }
        //bfs部分
        int index=0;
        while(!queue.isEmpty())
        {
            //将出度为0的结点全部出队
            for(int i=queue.size();i>0;i--)
            {
                //获取结点的下标,并出队
                Integer node=queue.poll();
                res[index++]=node;
                //遍历该结点到达了哪些结点,并将那些结点入度-1;
                for(Integer j:list.get(node))
                {
                    indeg[j]--;
                    //可以学习该课程了，入队
                    if(indeg[j]==0)
                    {
                        queue.add(j);
                    }
                }
            }
        }
        for(int i=0;i<numCourses;i++)
        {
            if(indeg[i]!=0)
                return new int[]{};
        }
        return res;

    }
}

630. 课程表 III

这里有 n 门不同的在线课程，按从 1 到 n 编号。给你一个数组 courses ，其中 courses[i] = [durationi, lastDayi] 表示第 i 门课将会持续上 durationi 天课，并且必须在不晚于 lastDayi 的时候完成。

你的学期从第 1 天开始。且不能同时修读两门及两门以上的课程。

返回你最多可以修读的课程数目。

示例 1：

输入：courses = [[100, 200], [200, 1300], [1000, 1250], [2000, 3200]]
输出：3
解释：
这里一共有 4 门课程，但是你最多可以修 3 门：
首先，修第 1 门课，耗费 100 天，在第 100 天完成，在第 101 天开始下门课。
第二，修第 3 门课，耗费 1000 天，在第 1100 天完成，在第 1101 天开始下门课程。
第三，修第 2 门课，耗时 200 天，在第 1300 天完成。
第 4 门课现在不能修，因为将会在第 3300 天完成它，这已经超出了关闭日期。

import java.util.Arrays;
import java.util.PriorityQueue;

//leetcode submit region begin(Prohibit modification and deletion)
class Solution {
    public int scheduleCourse(int[][] courses) {
        Arrays.sort(courses,(a,b)->a[1]-b[1]);
        PriorityQueue<Integer> queue=new PriorityQueue<>((a,b)->b-a);//耗时时间从大到小进行排序
        int s=0;
        for(int[] a:courses)
        {
            int b=a[0],e=a[1];
            queue.add(b);
            s+=b;
            while(s>e)
            {
                s-=queue.poll();
            }
        }
        return queue.size();
    }
}

1462. 课程表 IV

你总共需要上 numCourses 门课，课程编号依次为 0 到 numCourses-1 。你会得到一个数组 prerequisite ，其中 prerequisites[i] = [ai, bi] 表示如果你想选 bi 课程，你必须先选 ai 课程。

有的课会有直接的先修课程，比如如果想上课程 1 ，你必须先上课程 0 ，那么会以 [0,1] 数对的形式给出先修课程数对。

先决条件也可以是间接的。如果课程 a 是课程 b 的先决条件，课程 b 是课程 c 的先决条件，那么课程 a 就是课程 c 的先决条件。

你也得到一个数组 queries ，其中 queries[j] = [uj, vj]。对于第 j 个查询，您应该回答课程 uj 是否是课程 vj 的先决条件。

返回一个布尔数组 answer ，其中 answer[j] 是第 j 个查询的答案。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
输出：[false,true]
解释：课程 0 不是课程 1 的先修课程，但课程 1 是课程 0 的先修课程。

示例 2：

输入：numCourses = 2, prerequisites = [], queries = [[1,0],[0,1]]
输出：[false,false]
解释：没有先修课程对，所以每门课程之间是独立的。

import java.util.*;

class Solution {
    public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {
        int[] indeg=new int[numCourses];
        List<Boolean> res=new ArrayList<>();
        Boolean[][] grid=new Boolean[numCourses][numCourses];

        List<List<Integer>> list = new ArrayList<List<Integer>>();//邻接表存图
        for (int i = 0; i < numCourses; i++) {
            list.add(new ArrayList<>());
            grid[i]=new Boolean[numCourses];
            Arrays.fill(grid[i],false);
        }
        for (int i = 0; i < prerequisites.length; i++) {
            list.get(prerequisites[i][0]).add(prerequisites[i][1]);
            indeg[prerequisites[i][1]]++;
        }

        Queue<Integer> queue = new LinkedList<>();
        //先将入度为0入队
        for (int i = 0; i < numCourses; i++) {
            if (indeg[i] == 0)
                queue.add(i);
        }
        while (!queue.isEmpty()) {
            for (int i = queue.size(); i > 0; i--) {
                Integer node = queue.poll();
                for (Integer j : list
                     
                      .get(node)) {
                    grid[node][j]=true;
                    for(int k=0;k<numCourses;k++)
                    {
                        grid[k][j]=grid[k][j] || grid[k][node];
                    }
                    indeg[j]--;
                    if (indeg[j] == 0) queue.add(j);
                }
            }
        }
        for(int[] a:queries)
        {
            res.add(grid[a[0]][a[1]]);
        }
        return res;
    }


}

547. 省份数量

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中省份的数量。

示例 1：

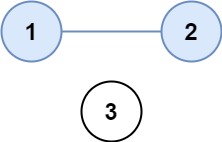
输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

//leetcode submit region begin(Prohibit modification and deletion)
class Solution {
    public int findCircleNum(int[][] isConnected) {
        int n=isConnected.length;
        List<List<Integer>> grid=new ArrayList<>();//邻接表
        //存图
        for(int i=0;i<n;i++) {
            grid.add(new ArrayList<>());
            for (int j = 0; j < n; j++) {
                if (isConnected[i][j] == 1)
                    grid.get(i).add(j);
            }
        }
        boolean[] visit=new boolean[n];
        int res=0;
        for(int i=0;i<n;i++)
        {
            Queue<Integer> queue=new LinkedList<>();
            if(visit[i]==false)
            {
                res++;
                visit[i]=true;
                queue.add(i);
                //bsf部分
                while(!queue.isEmpty())
                {
                    Integer node=queue.poll();
                    //遍历该结点连接的结点
                    for(Integer j:grid.get(node))
                    {
                        if(!visit[j])
                            queue.add(j);
                        visit[j]=true;
                    }
                }
            }
        }
        return res;
    }
}