目录

一、线性二自由度汽车模型（自行车模型）

1、二自由度模型概述

2、不同参考点下的状态空间方程

3、前向仿真

二、运动基元生成方法

1、杜宾斯曲线（Dubins Curve）

2、Reeds Shepp Curve

三、多项式曲线（Polynomial Curve）

1、五次多项式曲线（Quintic Polynomial）       

五次多项式曲线介绍

 五次多项式曲线应用

 2、螺旋线（Spiral Curve）

三次螺旋线 （Cubic Spiral Curve）

 辛普森方法（Simpson's method）

​编辑 参数重映射        

牛顿求根法（Newton's Method for Root Finding）

---

一、线性二自由度汽车模型（自行车模型）

1、二自由度模型概述

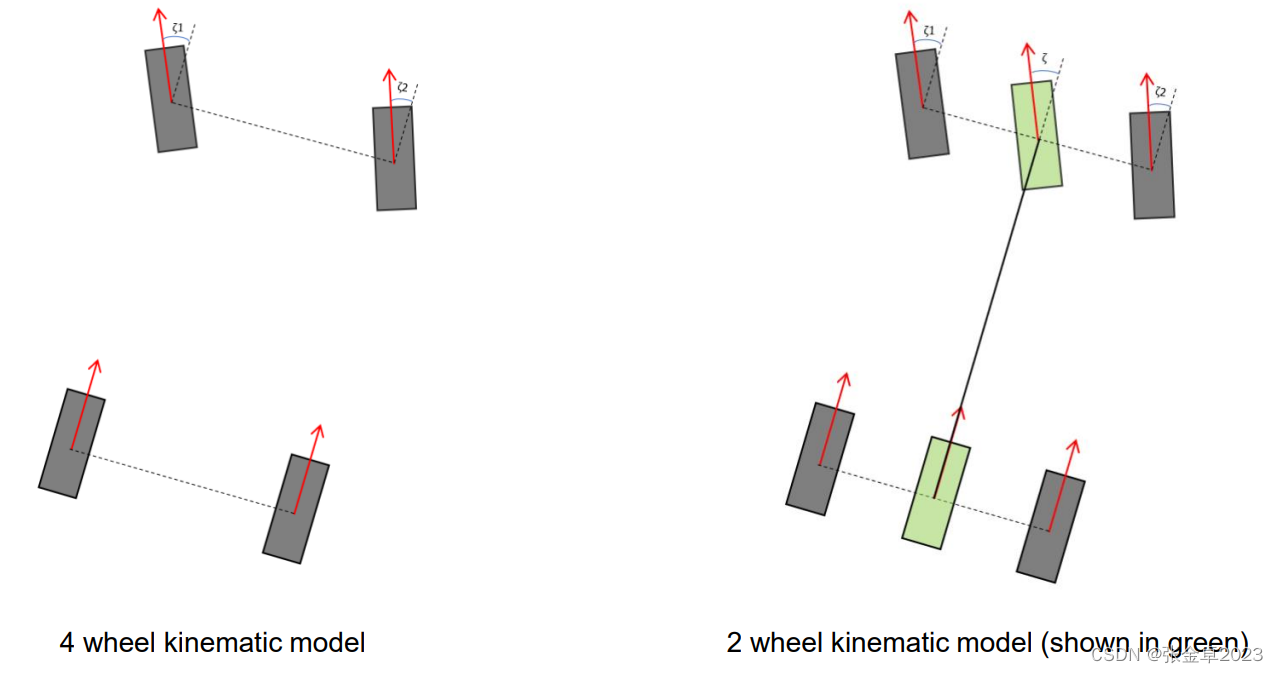
        如上图所示，左侧为传统的四轮汽车运动学模型，右侧为简化的二自由度汽车模型，仅保留沿着y轴的移动和绕z轴的横摆 。为了简化得到二自由度模型，需要满足一下几个基本假设：

• 车辆运动在二维平面上；
• 假设无滑移条件：轮胎没有横向或纵向滑移，因此我们可以假设车轮的速度与车轮的朝向一致。

2、不同参考点下的状态空间方程

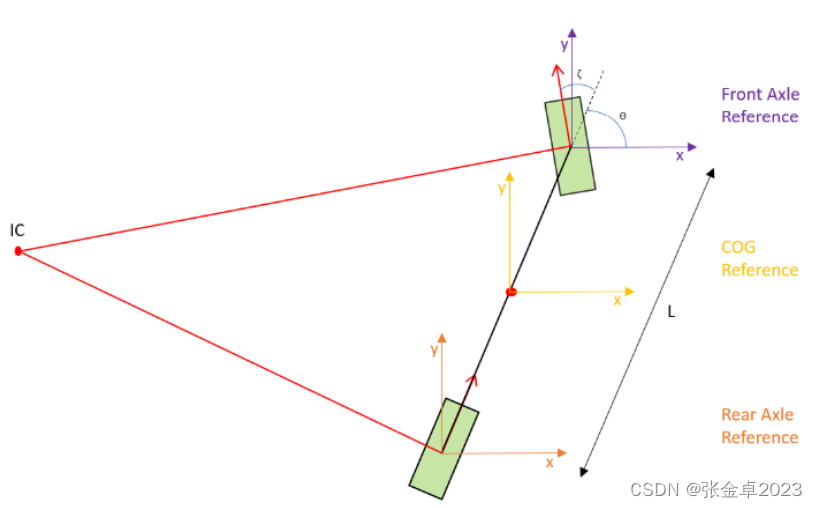
         在线性二自由度汽车模型中，可以以后轮中心为参考点，以前轮中心为参考点，或以整车质心为参考点。

①以后轮中心为参考点

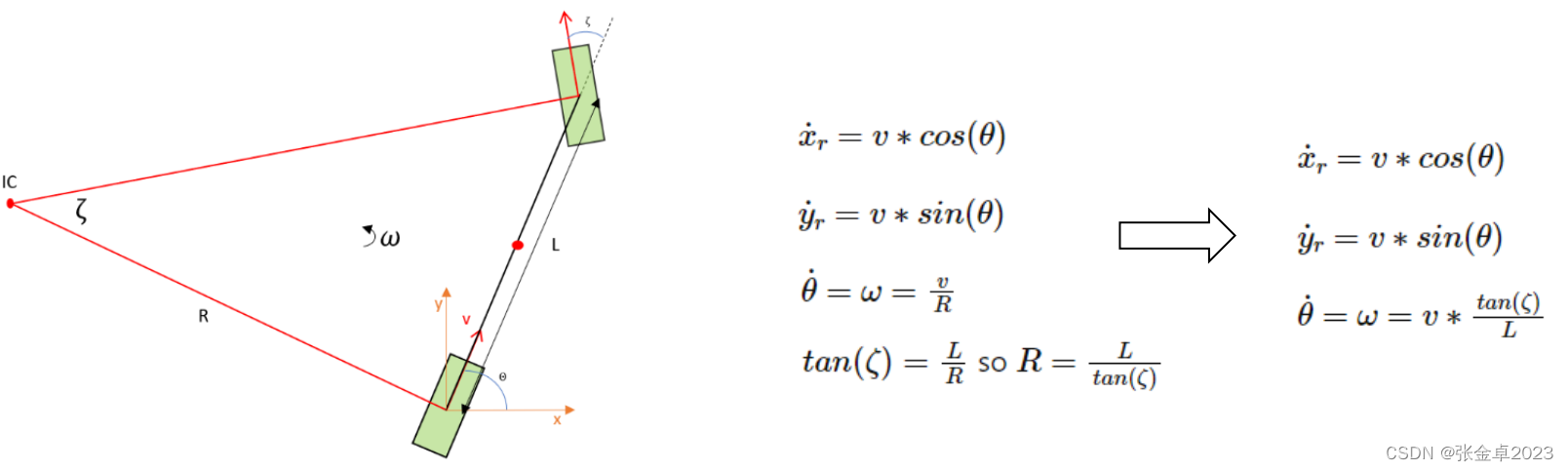
        从最后得到的公式可知，若已知车辆起始位置（x,y,θ），前轮偏转角ε和起始速度v就可以预测一定时间△t后的车辆所处的位置；

②以前轮中心为参考点

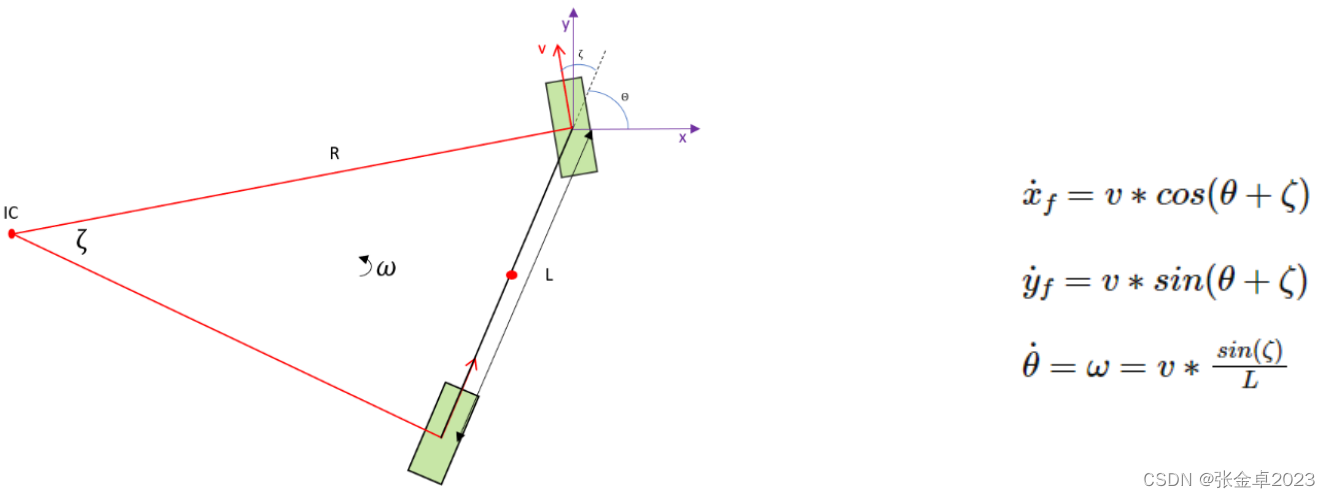
        以前轮中心为参考点进行分析与以后轮中心为参考点类似，只是角度发生了一些变化； 

③以质心为参考点

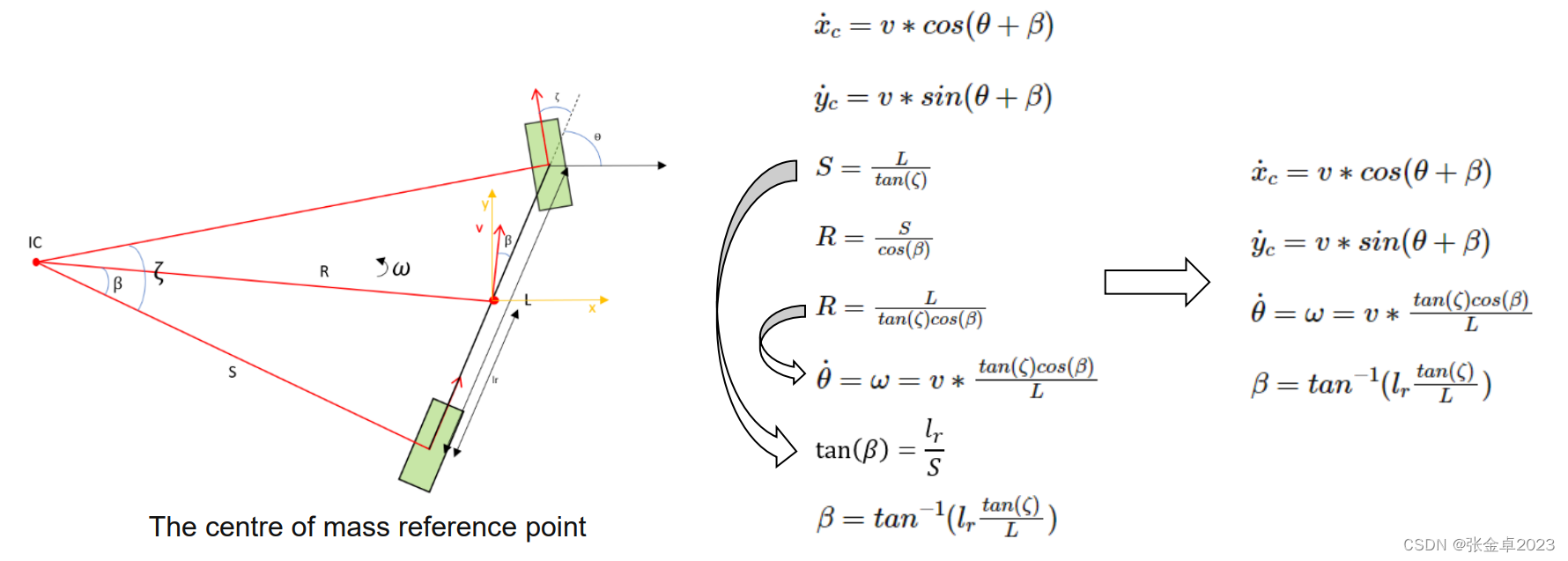        L是汽车的轴距，lr对应汽车后轴距（对应汽车质心到后轮中心的距离），β是汽车的航偏角。

3、前向仿真

        在自动驾驶规划领域中，前向仿真/积分是非常常用的一种方法，如果我们知道一组初始状态量、一组输入量并且给定一段时间就可以通过积分的方式得到下一个时刻汽车的状态量。对应下图所示的过程：

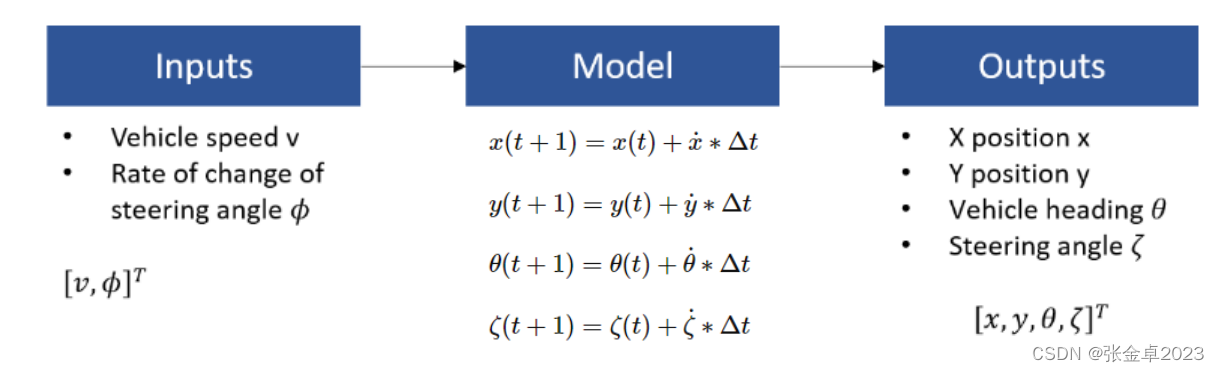
        需要注意的是输入量是车速和方向盘的转速，与前面介绍的微分方程状态量不同，如果直接传入方向盘转速（对应前轮偏转角ε），那么会使转向角瞬间发生变化，这与实际驾驶过程不符。显然用偏转角的变化率作为输入量更合理；

        前面推导出来的微分方程都是连续的，我们通常要利用离散的方法区评估一个连续的积分结果。上图介绍的就是较为经典的处理微分方程的数值方法——欧拉法，大致思想是利用梯形的面积来近似原函数的积分值。

二、运动基元生成方法

1、杜宾斯曲线（Dubins Curve）

        杜宾斯曲线的目的是要求解二维平面上两个位姿之间的最短路径。

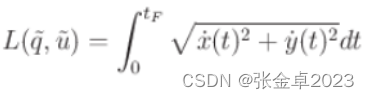
        当车辆运动速度恒定时，系统可被简化为：        

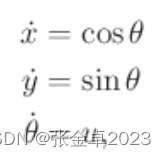
       转角u的取值从区间[-tanφmax, tanφmax]中选择，由于在日常生活中车辆的前轮转角大多在[-π/2, π/2]之间，因此为了简化可以取tanφ = 1。

        在任意两个位姿之间，车辆的杜宾斯曲线总是可以被不超过三个运动基元的组合表示出来，分别被记为S（直行）、L（向左以最大转角行驶得到的圆弧）和R（向右以最大转角行驶得到的圆弧）。

         杜宾斯曲线证明了只有一下六种组合能够取得最优解，任意两个位姿之间的最短路径总是可以用其中一个组合来表示。

{LRL, RLR, LSL, LSR, RSL, RSR}

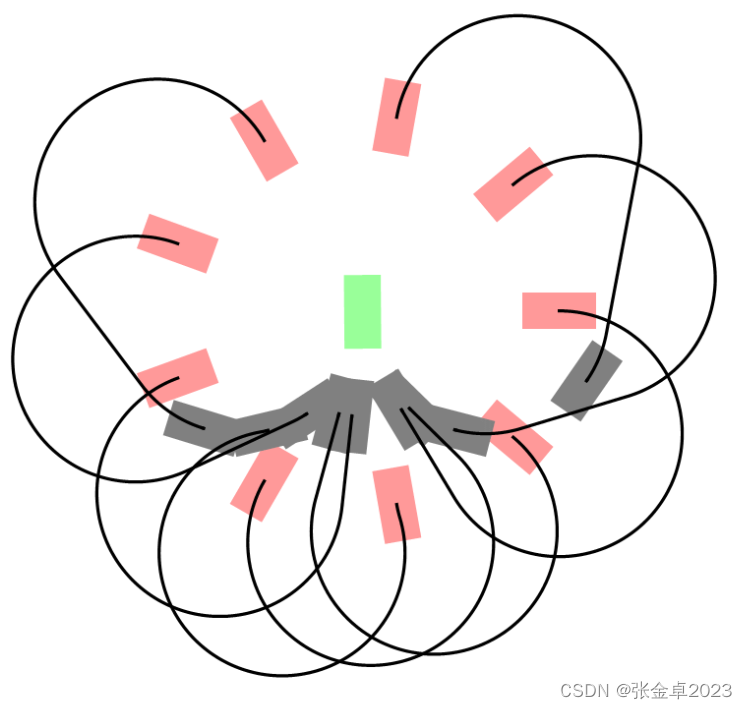
        以下图为例描述车辆沿杜宾斯曲线的运动轨迹：

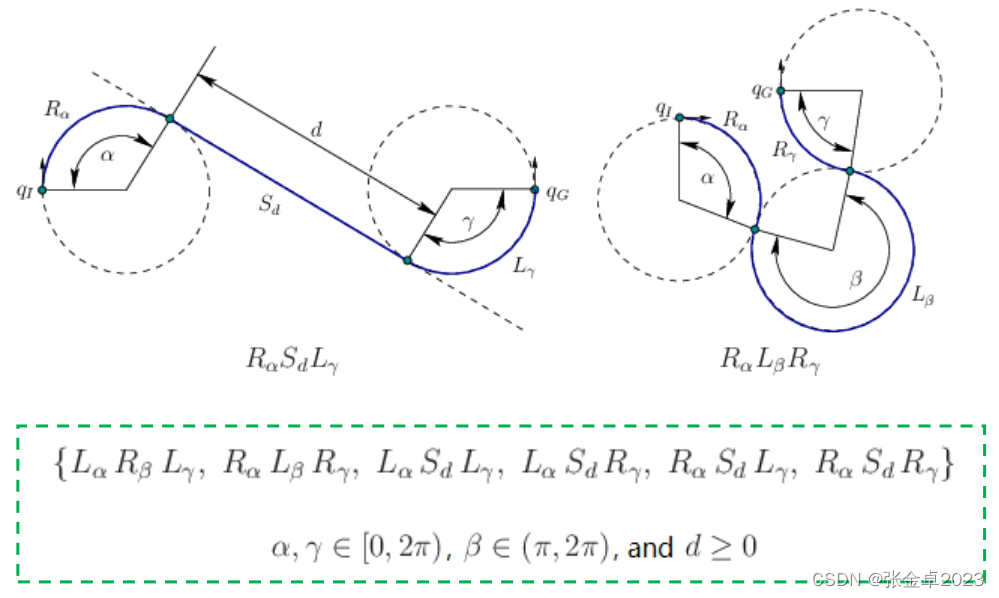
        以左侧的杜宾斯曲线为例，一开始的Rα表示车辆向右行驶过一段α圆心角的弧长，第二段Sd表示的是在直行过程中行驶出来的距离d，第三段Lγ表示车辆向左行驶过一段γ圆心角的弧长。

        图中还需要注意β的取值与α、γ不同，β的取值不能低于π，因为杜宾斯曲线证明若β的取值低于π，那么一定会有另一种运动基元的组合取得最优解。

        对于给定起始点和终点，利用杜宾斯曲线进行最短路劲求解仍然面临两个问题：

• 以上六种运动基元的组合哪个能够获得最短路劲？
• 如何获取下标α、β、γ和d的值？

        对于第一个问题，可以尝试将六种组合一一尝试的方式，或者利用解析解的方式进行求解；

        第二个问题则需要理由各种几何关系进行求解，目前编程上也存在直接可以使用的库函数对杜宾斯曲线的参数进行求解。

2、Reeds Shepp Curve

        Reeds Shepp Curve和Dubins Curve整体上十分类似，唯一的区别是Dubins Curve只允许车辆做正向运动，而Reeds Shepp Curve允许车辆做反向运动。

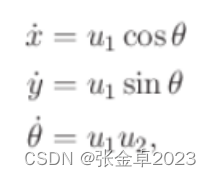
        体现到微分方程中， Reeds Shepp Curve利用u1和u2两个参数来表示车辆的运动方向，u1表示车辆的前后运动，u2表示车辆的左右运动；

        u1的取值为{-1, 1}，分别表示向后和向前，u2的取值为[-tanφmax, tanφmax]，为了简化u2依然可以只在区间[-1, 1]之间进行取值。

        Reeds Shepp Curve被证明有不超过48种的组合可以用来描述车辆的最短路径，如下表所示：

三、多项式曲线（Polynomial Curve）

1、五次多项式曲线（Quintic Polynomial）       

五次多项式曲线介绍

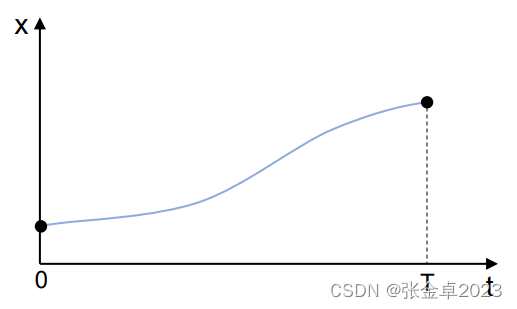
        假设在某个时刻t的一维运动x(t)被表述为五次多项式

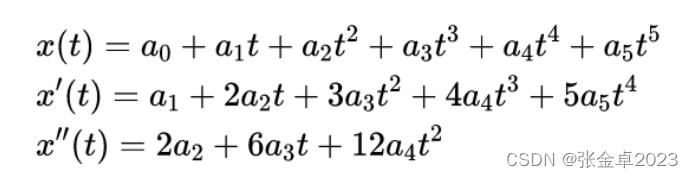
        在五次多项式中共有六个未知量a0……a5，因此要求解一条五次多项式只需要构造出六个等式方程即可，在自动驾驶中通常将起始点和终点作为边界条件。

        具体来说可假设起始点时t = 0，终点时t = T，那么对于一条五次多项式可以进行如下求解：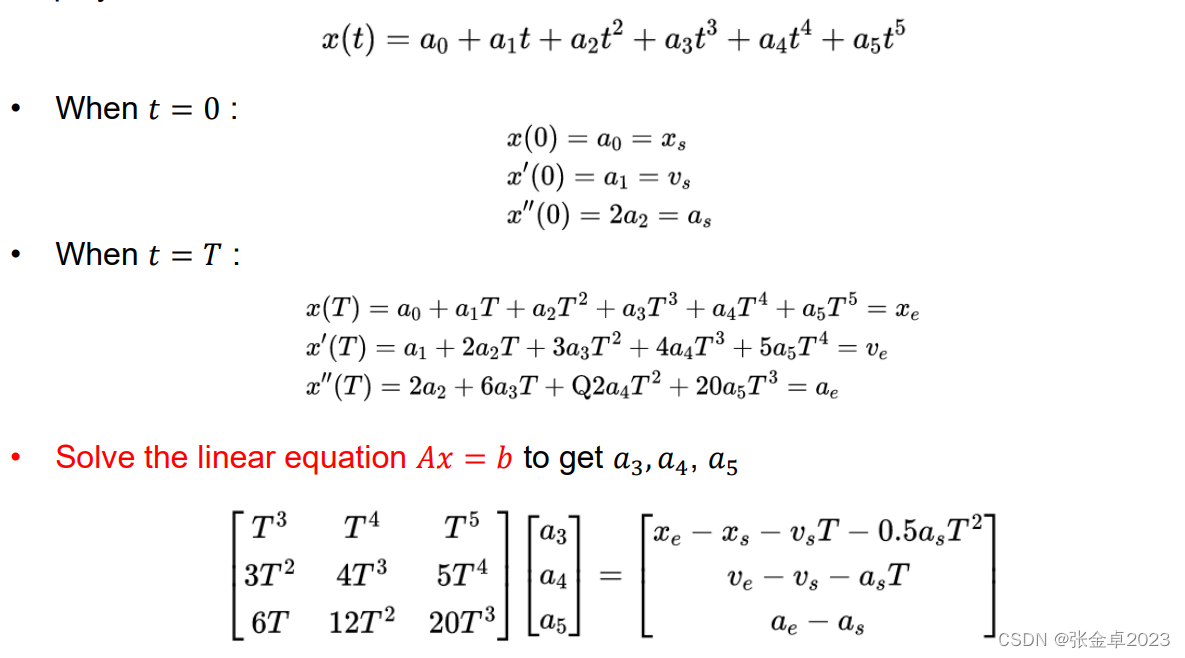

 五次多项式曲线应用

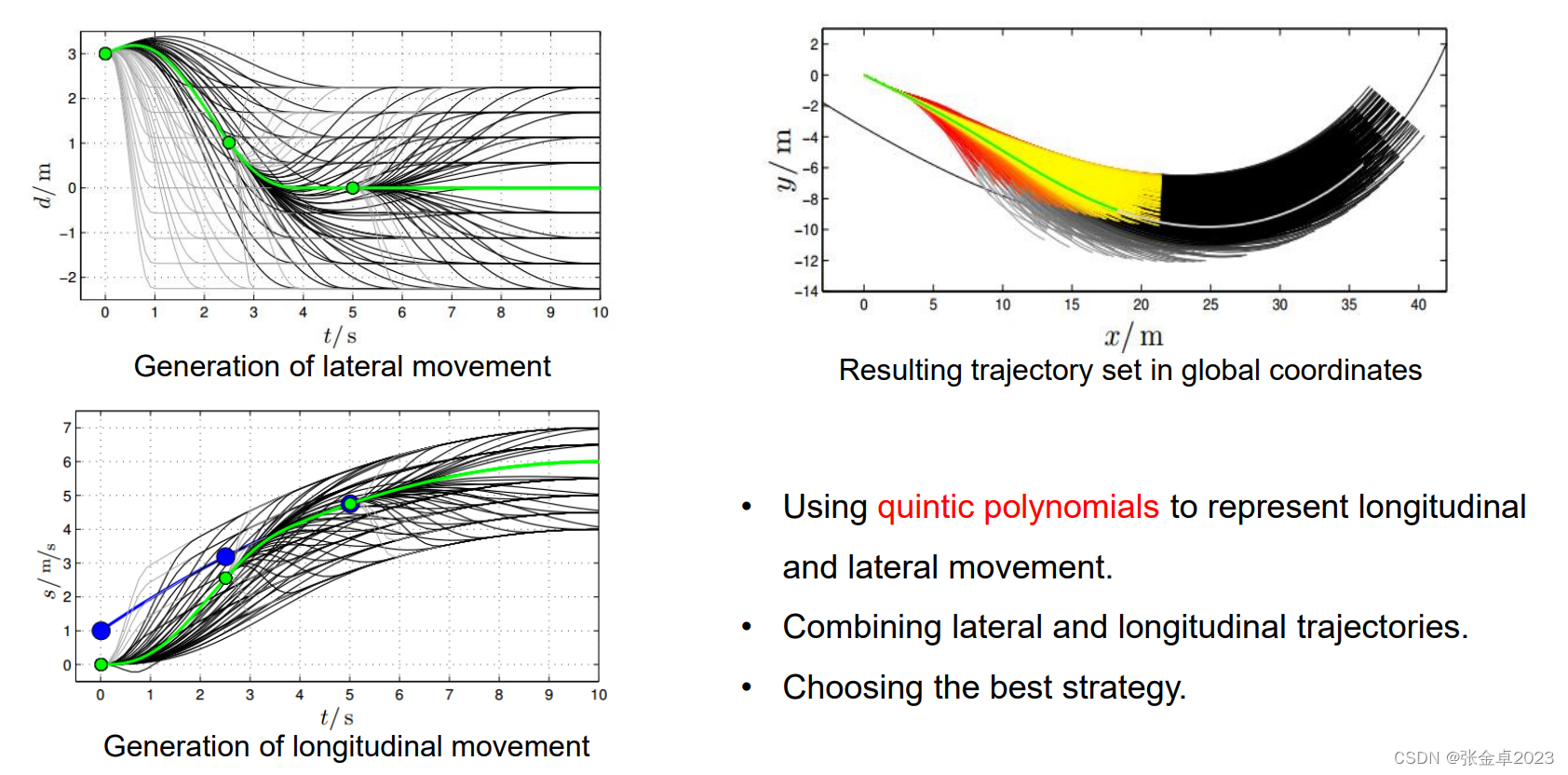
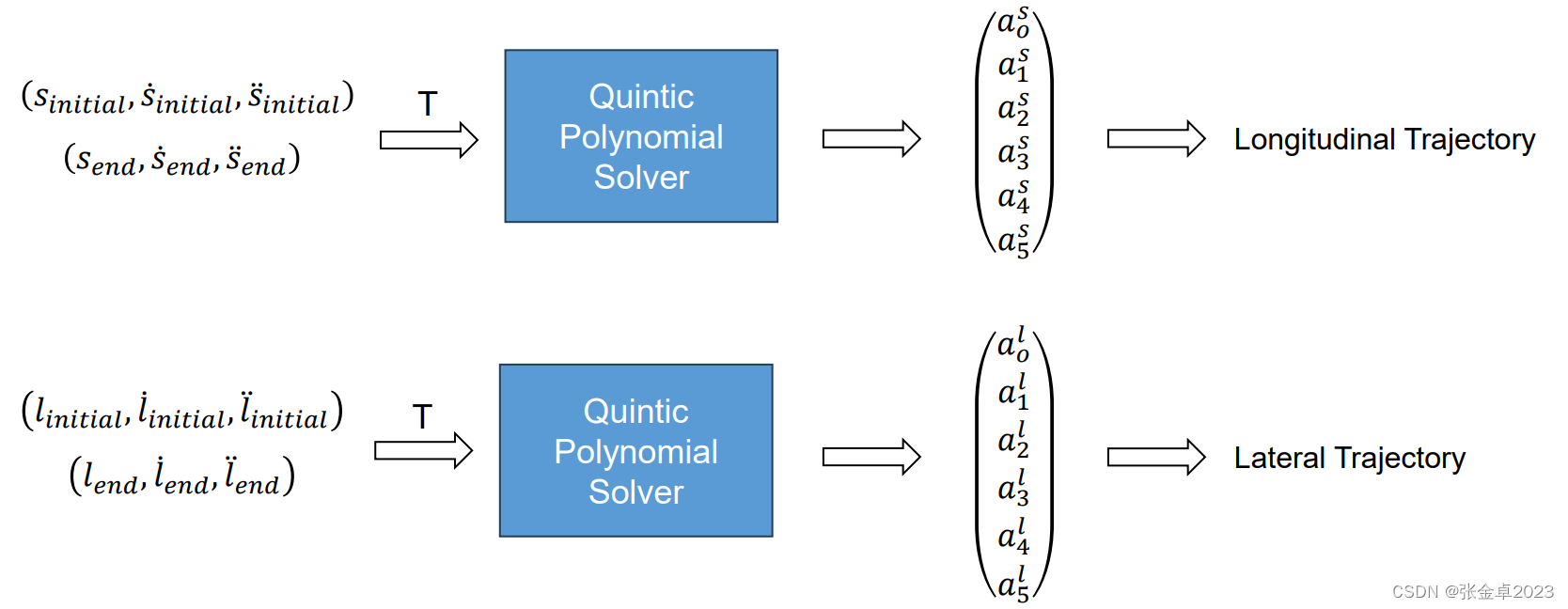
        上图左侧是在frenet坐标系中利用五次多项式曲线去描述纵向和侧向运动， 对于侧向和纵向运动，都给定初始的状态量，通过采样的方式取得一系列终点的状态量，利用上述的计算方式获得对应起始点和终止点的五次多项式曲线。

        图中浅灰色的曲线是一些被过滤的不合理的五次多项式曲线，在符合约束条件的五次多项式曲线中按照特定的cost获取最优的曲线（图中用绿色表示）。

        将采样得到的侧向和纵向方向的五次多项式按照cost加权的方式进行组合就能得到如上图右侧所示的综合曲线，然后在合并后的曲线中选择最优的曲线。

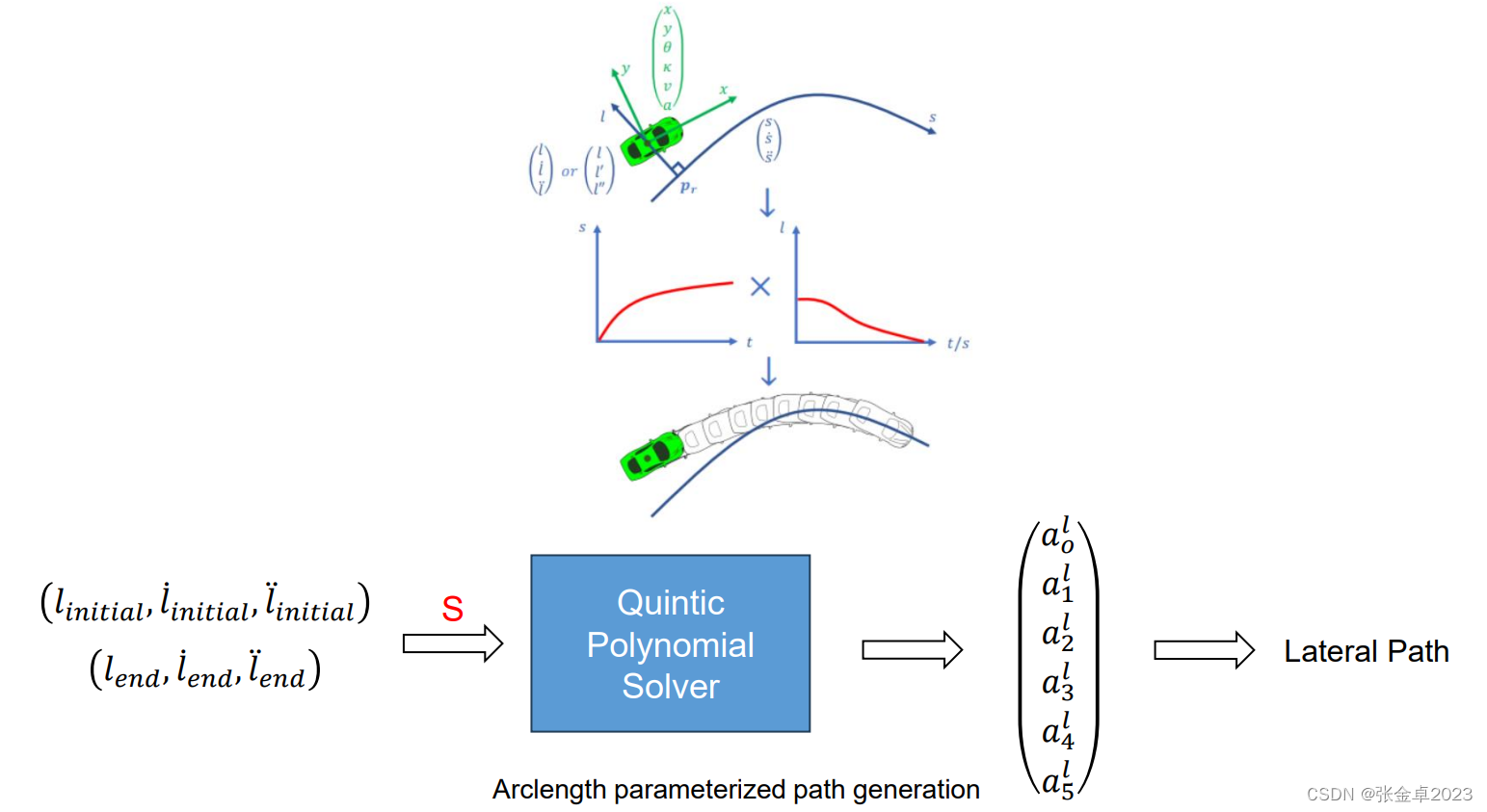
         前面讲过在frenet坐标系中规划的方法，车辆的侧向运动有两种参数化的表述形式，第一种是以时间t为参数化l(t)，对应上面介绍的应用，还有一种是以弧长s为参数化l(s)，下图介绍的是五次多项式在这种自动驾驶场景的应用：

 2、螺旋线（Spiral Curve）

三次螺旋线 （Cubic Spiral Curve）

        三次螺旋线与上面介绍的五次多项式都是用来解决路径边界问题（bvp, Path boundary value problem）的方法，所谓bvp问题就是给定起点和终点约束来获取一条参数化曲线。

        螺旋线是关于曲率对弧长的函数k(s)，表示为随着弧长的变化，每一点所对应的曲率大小。本节以三次螺旋线为例进行介绍。

        通过质点的运动学模型可以得到以下表达式：

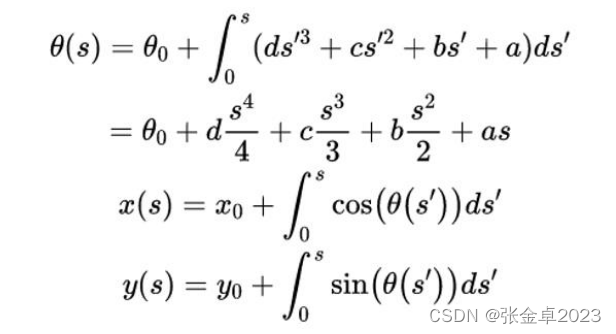
        对于θ值可以通过上述解析的方式求得，但是对于x和y的值的获取就比较复杂了。在数学上，形如 的函数叫做菲涅尔积分，无法通过解析的方式获得位置的闭合解

        因此我们需要使用一些数值近似的方法来评估菲涅尔积分的值。一种常用的方法叫做辛普森方法（Simpson's method）。

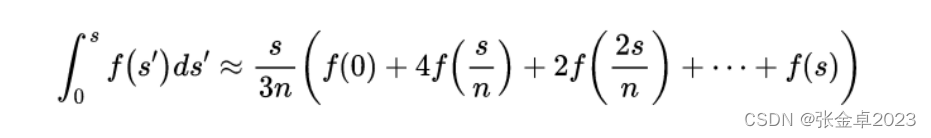
 辛普森方法（Simpson's method）

        辛普森方法是一种利用二次函数来近似估计定积分值的方法，如下图 所示，辛普森法则可以通过用二次插值函数P(x)逼急被积函数f(x)来推导。

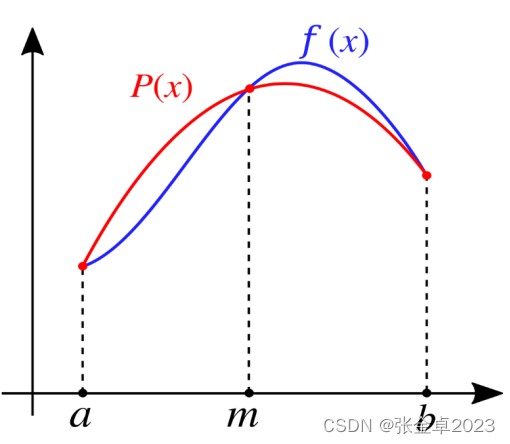
         为了通过辛普森方法获取定积分的近似值，我们通常会将[a, b]区间划分为偶数个子区间，每一个子区间的宽度为△x = (b - a) / n；

        在每一个连续的子区间上，我们考虑用二次函数穿过子区间的端点值

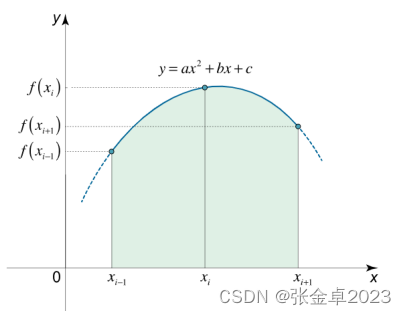
        对应的计算表达式为：

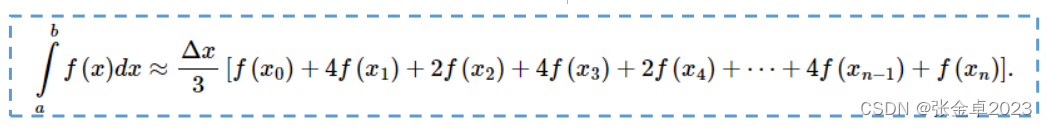
        辛普森法则计算公式的系数满足一下规律：

         辛普森方法相比于其他简单的数值方法（如中点法、梯形法）更加的精确，因为相比于中点法梯形法那种化曲为直的思想，用二次函数的曲线更加贴合定积分的曲线。 分割得到的子区间个数n会直接影响到积分近似的精确度和效率。

• 一般来讲，随着n的增大，我们能够得到更加准确的近似值；
• 与此同时，随着n的增大，计算所消耗的资源也越大，效率降低。

        下面以n=8为例在三次螺旋曲线中应用辛普森方法：

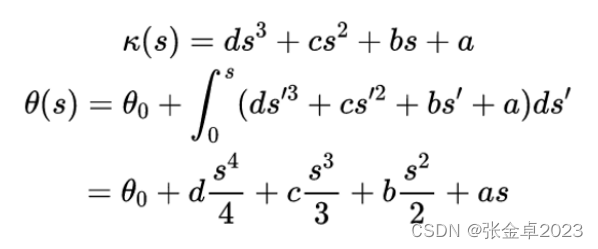
        将辛普森方法应用于x(s)和y(s)的求解

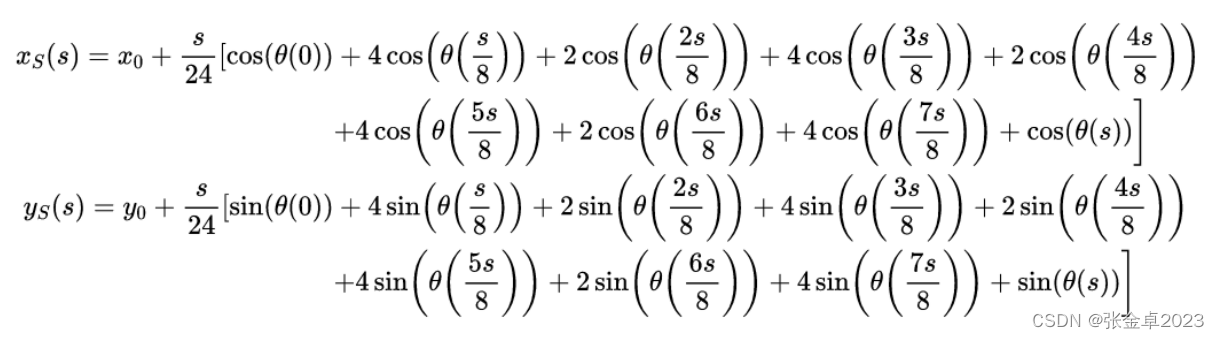 参数重映射        

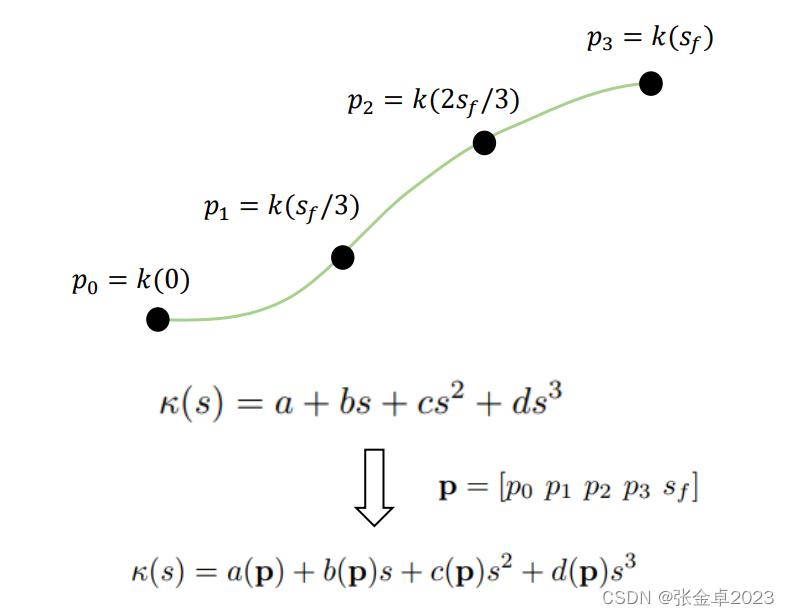
       参数重映射的思想是将原函数中的参数转化为p的向量，向量有五个维度组成分别为p0, p1, p2, p3, sf。

        p0,...,p3分别表示在整条曲线上按等弧长取到的四个点，sf则表示整条曲线的弧长，代入重映射后的三次螺旋线中得到：

         最终可以得到新得到的参数关于相邻p中的各维度的表达式：

         虽然原函数中只有四个参数，重映射后增加到了五个参数，但是p0和p3表示的是起点和终点的曲率，是已知量，函数就降到了三维，相比与原函数降低了一个维度。

        重映射后的公式能够确保各参数pi在量级上较为接近，为优化增加了数值稳定性。

        而对于剩下三个参数的求解，又要用到一种新的方法——牛顿求根法（Newton's Method for Root Finding）。

牛顿求根法（Newton's Method for Root Finding）

         先假设出采用参数p在终点处的向量：

        在参数重映射后 ，重点的k(sf)是已知输入量，因此我们要求解的状态输入量只有x、y和θ三个维度，向量p是优化后想要求解的变量。

        整个优化目标是我们希望的终点状态量和期望的状态量相等：

         再生成雅可比矩阵，使用牛顿寻根法生成p的估计序列：

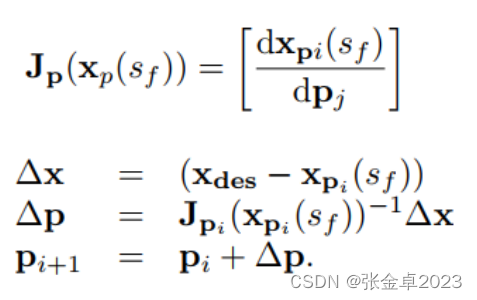
        式中△x、△p表示梯度下降的方向，Pi+1是下一次迭代。

        下面对牛顿寻根法做一个简要的描述：

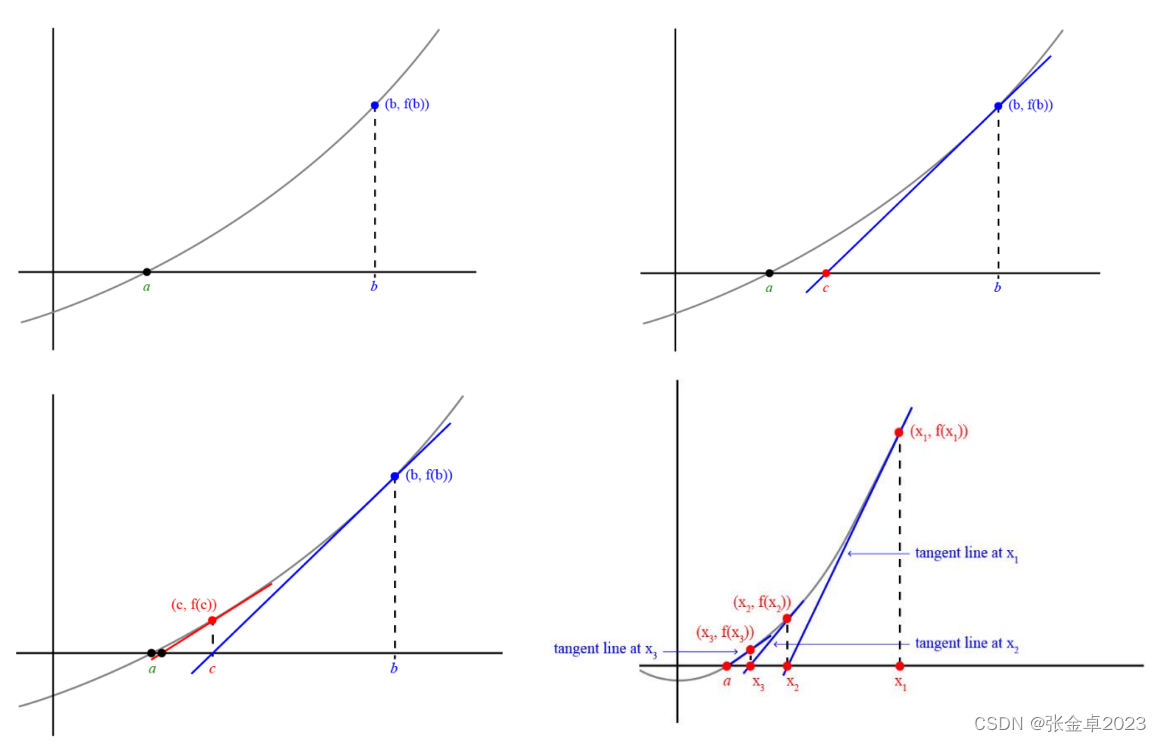
       上图是牛顿寻根法在一维函数中应用的一个直观体现。大致思想是：从一个初始的猜测开始，然后用它的切线来近似函数，最后计算这个切线的x轴截距。这个x截距通常会比第一次猜测更接近原始函数的根，迭代直到找到解。

        迭代公式为：

        对于牛顿求根法，初值的选取是比较重要的，它会直接影响到最终求得的解是否为当前周期内的全局最优解，有两个可以采取的策略：

• 通过查表的方式获取
• 从上一个规划周期中导出类似位置的端点对。

        利用螺旋线的优点是可以显式地约束曲率以及曲率高阶量的信息，可以使得整条曲线更光滑，但是所消耗的计算资源也是比较大的。