递推可以说是递归反过来的一种算法,递归是从后往前倒着算,递推是从前往后正着算。

统计每个月兔子的总数
题目描述
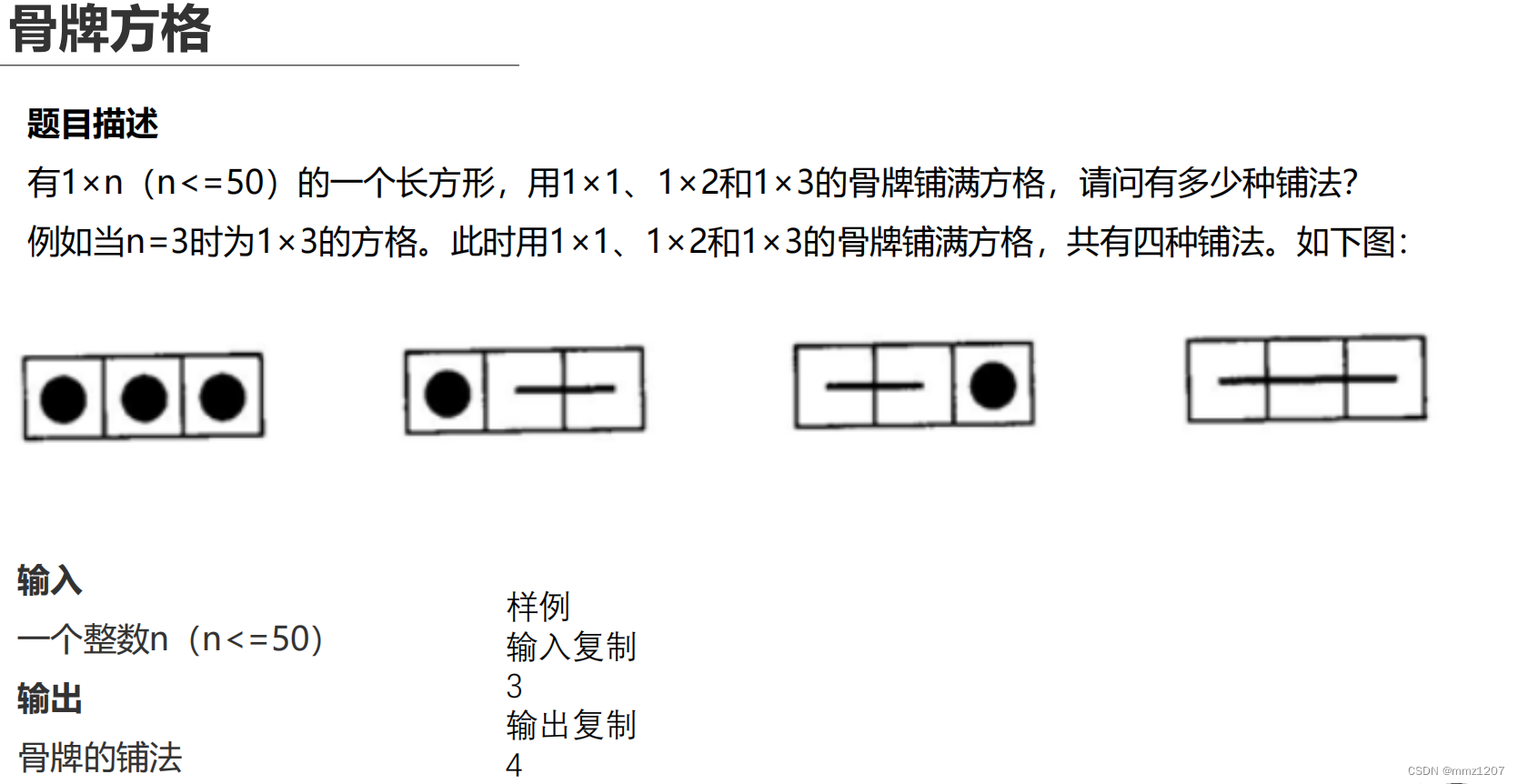
有一对兔子,从出生后第3个月起每个月都生一对兔子,一对小兔子长到第三个月后每个月又生一对兔子,
假如兔子都不死,问第n个月(n<=50)的兔子总数为多少对?
输入
输入1个整数n,表示第几个月
输出
第n个月兔子的总数量有多少对?
样例
输入复制
9
输出复制
34
#include <bits/stdc++.h>
using namespace std;
int main()
{
long long a[100];
a[0] = 1;
a[1] = 1;
int n;
cin>>n;
cout<<1<<endl<<1<<endl;
for(int i = 2;i<n;i++)
{
a[i] = a[i-1]+a[i-2];
cout<<a[i]<<endl;
}
return 0;
}
猴子吃桃子
题目描述
猴子吃桃子问题:猴子第一天摘下若干个桃子,当即吃了一半还不过瘾,又多吃了一个;第二天又
将剩下的桃子吃掉一半又多吃了一个;以后每天早上都吃了前一天剩下的一半零一个。到了第十天
想再吃时,见只剩下一个桃子,求第一天共摘了多少个桃子?
输入
无
输出
一个整数,第一天共有多少个桃子
#include <bits/stdc++.h>
using namespace std;
int main()
{
long long a[20];
a[10] = 1;
for(int i = 9;i>=1;i--)
{
a[i] = (a[i+1]+1)*2;
}
cout<<a[1];
return 0;
}
#include <bits/stdc++.h>
using namespace std;
int main()
{
long long a[110],b;
a[1] = 1;
int n;
cin>>n;
b = 1;
for(int i = 2;i<=n;i++)
{
a[i] = a[i-1]+i;
b = b+a[i];
}
cout<<b;
return 0;
}
Pell数列
题目描述
有一种数列,它的前10项的值分别为:1 2 5 12 29 70 169 408 985 2378,这个数列被称
为Pell数列,请问该数列的第n项的值是多少?(n<=1000)
输入
一个整数n。
输出
第n项的值。
样例
输入复制
10
输出复制
2378
青少年编程
#include <bits/stdc++.h>
using namespace std;
int main()
{
long long a[1010];
int n;
cin>>n;
a[1] = 1;
a[2] = 2;
for(int i = 3;i<=n;i++)
{
a[i] = a[i-1]*2+a[i-2];
}
cout<<a[n];
return 0;
}
上台阶
描述
楼梯有n(30 > n > 0)阶台阶,上楼时可以一步上1阶,也可以一步上2阶,也可以一
步上3阶,编程计算共有多少种不同的走法。
输入
输入的每一行包括一组测试数据,即为台阶数n。最后一行为0,表示测试结束。
输出
每一行输出对应一行输入的结果,即为走法的数目。
样例输入
1
2
3
4
0
样例输出
1
2
4
7
#include <bits/stdc++.h>
using namespace std;
int main()
{
long long a[1010];
int b[50];
int n;
for(int i = 0;true;i++)
{
int t;
cin>>t;
if(t==0)
{
n = i;
break;
}
b[i] = t;
}
a[1] = 1;
a[2] = 2;
a[3] = 4;
for(int i = 4;i<=30;i++)
{
a[i] = a[i-1]+a[i-2]+a[i-3];
}
cout<<endl;
for(int i = 1;i<=n;i++)
{
cout<<a[i]<<endl;
}
return 0;
}
#include <bits/stdc++.h>
using namespace std;
int main()
{
long long a[110];
int m,n;
cin>>m>>n;
n = n-m+1;
a[1] = 1;
a[2] = 1;
for(int i = 3;i<=n;i++)
{
a[i] = a[i-1]+a[i-2];
}
cout<<a[n];
return 0;
}
#include <bits/stdc++.h>
using namespace std;
int main()
{
long long a[100];
a[1] = 1;
a[2] = 2;
a[3] = 4;
int n;
cin>>n;
for(int i = 4;i<=n;i++)
{
a[i] = a[i-1]+a[i-2]+a[i-3];
}
cout<<a[n];
return 0;
}
(此题有不用递推的其他简便方法)
#include <bits/stdc++.h>
using namespace std;
int main()
{
int m,n;
cin>>m>>n;
if((m*n)%2==0)
{
cout<<m*n/2;
}
else
{
cout<<(m*n-1)/2;
}
return 0;
}
#include <bits/stdc++.h>
using namespace std;
int main()
{
long long a[10010];
a[1] = 2;
a[2] = 4;
a[3] = 8;
int n;
cin>>n;
for(int i = 4;i<=n;i++)
{
a[i] = a[i-1]+a[i-2]+a[i-3];
}
cout<<a[n];
return 0;
}
菲波那契数列(2)
描述
菲波那契数列是指这样的数列: 数列的第一个和第二个数都为1,接下来每个数都
等于前面2个数之和。 给出一个正整数a,要求菲波那契数列中第a个数对1000取
模的结果是多少。
输入
第1行是测试数据的组数n,后面跟着n行输入。每组测试数据占1行,包括一个正
整数a(1 <= a <= 1000000)。
输出
n行,每行输出对应一个输入。输出应是一个正整数,为菲波那契数列中第a个数
对1000取模得到的结果。
样例输入
4
5
2
19
1
样例输出
5
1
181
1
#include <bits/stdc++.h>
using namespace std;
long long a[1000010];
int main()
{
int b[10000];
int n;
cin>>n;
for(int i = 0;i<n;i++)
{
cin>>b[i];
}
a[1] = 1;
a[2] = 1;
for(int i = 3;i<=1000000;i++)
{
a[i] = (a[i-1]+a[i-2])%1000;
}
cout<<endl;
for(int i = 0;i<n;i++)
{
cout<<a[b[i]]<<endl;
}
return 0;
}