活动 - AcWing
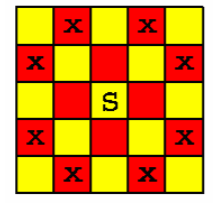
在一个 n∗n 个方格的国际象棋棋盘上,马(骑士)可以攻击的棋盘方格如图所示。
棋盘上某些方格设置了障碍,骑士不得进入。
对于给定的 n∗n个方格的国际象棋棋盘和障碍标志,计算棋盘上最多可以放置多少个骑士,使得它们彼此互不攻击。
输入格式
第一行有 2 个正整数 n 和 m,分别表示棋盘的大小和障碍数。
接下来的 m 行给出障碍的位置。每行 2 个正整数,表示障碍的方格坐标。
输出格式
输出可以共存的最大骑士数量。
数据范围
1≤n≤200,
0≤m<n2
输入样例:
3 2
1 1
3 3
输出样例:
5解析:
本题是要求放最多的马使得所有马不会相互攻击,如果将所有能相互攻击的马之间连一条边,将所有奇数格作为左部节点,将所有偶数格作为右部节点,这就是一个二分图,且要求选中的点之间都不存在边,也就是求二分图的最大独立集,可以用匈牙利算法来求。
但是本题的数据比较大,用匈牙利算法会被卡常数,因此需要用更快的算法实现,可以用网络流求最大权独立集的方法来求,而 dinic 算法比匈牙利算法快很多,不用担心超时。
最大权独立集 = 总权值 − 最小权点覆盖集,因此我们需要求出最小权点覆盖集,用固定做法就行,从源点向所有左部节点连一条容量是权值的边,从所有右部节点向汇点连一条容量是权值的边,左部节点和右部节点之间的边容量是 +∞。最小割就是最小权点覆盖。
本题每个点是没有权值的,求的也是最大独立集的点数,因此可以认为每个点的权值都是 1。这样就能求出最小点覆盖的点数,对应求出最大独立集的点数,两者是互补的。
作者:小小_88
链接:https://www.acwing.com/solution/content/133616/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
#include<unordered_set>
#include<bitset>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
const int N = 4e4 + 10, M = (N*8+2*N) * 2 + 10, INF = 0x3f3f3f3f;
int n, m, S, T;
int h[N], e[M], f[M], ne[M], idx;
int q[N], d[N], cur[N];
bool g[210][210];
void add(int a, int b, int c) {
e[idx] = b, f[idx] = c, ne[idx] = h[a], h[a] = idx++;
e[idx] = a, f[idx] = 0, ne[idx] = h[b], h[b] = idx++;
}
int get(int a, int b) {
return (a - 1) * n + b;
}
bool bfs() {
int hh = 0, tt = 0;
memset(d, -1, sizeof d);
q[0] = S, d[S] = 0, cur[S] = h[S];
while (hh <= tt) {
int t = q[hh++];
for (int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
if (d[j] == -1 && f[i]) {
d[j] = d[t] + 1;
cur[j] = h[j];
if (j == T)return 1;
q[++tt] = j;
}
}
}
return 0;
}
int find(int u, int limit) {
if (u == T)return limit;
int flow = 0;
for (int i = cur[u]; i != -1 && flow < limit; i = ne[i]) {
int j = e[i];
cur[u] = i;
if (d[j] == d[u] + 1 && f[i]) {
int t = find(j, min(f[i], limit - flow));
if (!t)d[j] = -1;
f[i] -= t, f[i ^ 1] += t, flow += t;
}
}
return flow;
}
int dinic() {
int ret = 0, flow = 0;
while (bfs())while (flow = find(S, INF))ret += flow;
return ret;
}
int main() {
cin >> n >> m;
memset(h, -1, sizeof h);
S = 0, T = n * n + 1;
for (int i = 1, a, b; i <= m; i++) {
scanf("%d%d", &a, &b);
g[a][b] = 1;
}
int tot = 0;
int dx[] = { -1,-2,-2,-1,1,2,2,1 }, dy[] = { -2,-1,1,2,2,1,-1,-2 };
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (g[i][j])continue;
if (i + j & 1) {
add(S, get(i, j), 1);
for (int k = 0; k < 8; k++) {
int x = i + dx[k], y = j + dy[k];
if (x > 0 && x <= n && y > 0 && y <= n&&!g[x][y]) {
add(get(i, j), get(x, y), INF);
}
}
}
else add(get(i, j), T, 1);
tot++;
}
}
cout << tot - dinic() << endl;
return 0;
}