44、二叉搜索树中第K小的元素
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)。
示例 1:
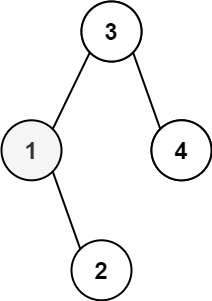
输入:root = [3,1,4,null,2], k = 1
输出:1
示例 2:

输入:root = [5,3,6,2,4,null,null,1], k = 3
输出:3
提示:
- 树中的节点数为
n。 1 <= k <= n <= 1040 <= Node.val <= 104
思路解答:
- 按照中序遍历的顺序遍历二叉搜索树,同时更新k的值。如果k的值为0,则返回当前节点的值。
def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
def inorder(node):
nonlocal k
if not node:
return None
val = inorder(node.left)
if val is not None:
return val
k -= 1
if k == 0:
return node.val
return inorder(node.right)
return inorder(root)
45、二叉树的右视图
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1:
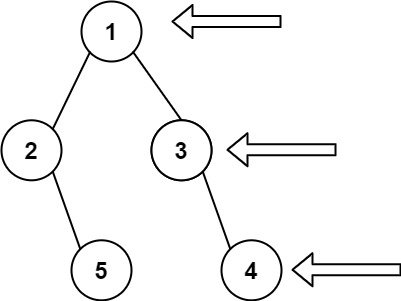
输入: [1,2,3,null,5,null,4]
输出: [1,3,4]
示例 2:
输入: [1,null,3]
输出: [1,3]
示例 3:
输入: []
输出: []
提示:
-
二叉树的节点个数的范围是
[0,100] -
-100 <= Node.val <= 100
思路解答:
1、使用BFS(广搜)遍历二叉树,每层从左到右遍历节点。
2、在每一层中,只保留该层最右侧的节点值。
def rightSideView(self, root: Optional[TreeNode]) -> list[int]:
if not root:
return []
result = []
queue = collections.deque([root])
while queue:
level_size = len(queue)
for i in range(level_size):
node = queue.popleft()
if i == level_size - 1:
result.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return result
46、二叉树展开为链表
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用
TreeNode,其中right子指针指向链表中下一个结点,而左子指针始终为null。 - 展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例 1:
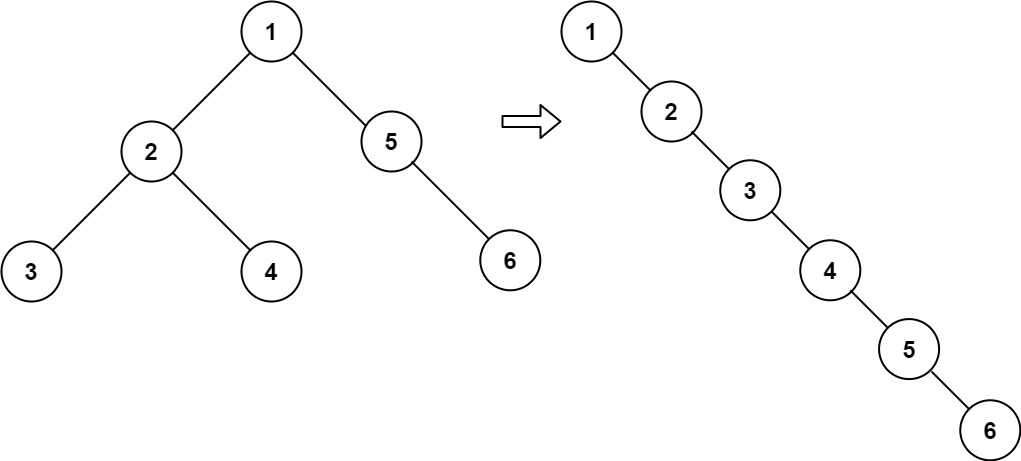
输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [0]
输出:[0]
提示:
- 树中结点数在范围
[0, 2000]内 -100 <= Node.val <= 100
思路解答:
- 将左子树插入到右子树的地方
- 将原来的右子树接到左子树的最右边节点
- 考虑新的右子树的根节点,一直重复上边的过程,直到新的右子树为 null
def flatten(self, root: Optional[TreeNode]) -> None:
if not root:
return
flatten(root.left)
flatten(root.right)
temp = root.right
root.right = root.left
root.left = None
while root.right:
root = root.right
root.right = temp
47、从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
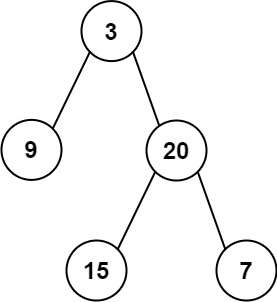
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
提示:
1 <= preorder.length <= 3000inorder.length == preorder.length-3000 <= preorder[i], inorder[i] <= 3000preorder和inorder均 无重复 元素inorder均出现在preorderpreorder保证 为二叉树的前序遍历序列inorder保证 为二叉树的中序遍历序列
思路解答:
- 先序遍历的第一个元素是根节点的值。
- 在中序遍历中找到根节点的位置,根节点左边的元素是左子树的中序遍历,右边的元素是右子树的中序遍历。
- 根据中序遍历中根节点的位置,可以确定左子树和右子树的节点数量。
- 在先序遍历中,根节点后面的若干元素对应左子树的先序遍历,再后面的元素对应右子树的先序遍历。
- 递归地构建左子树和右子树。
def buildTree(self, preorder: list[int], inorder: list[int]) -> Optional[TreeNode]:
if not preorder or not inorder:
return None
#preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
root_val = preorder[0]
root = TreeNode(root_val)
root_index = inorder.index(root_val)
root.left = buildTree(preorder[1:1 + root_index], inorder[:root_index])
root.right = buildTree(preorder[1 + root_index:], inorder[root_index + 1:])
return root