目录

一、B-树

二、B+树

三、B*树

四、时间复杂度

五、Mysql与B树系列

---

一、B-树

        首先再说B树的性质以及其他的之前，先要说一声，好多人都把这个树叫B减树，其实不是，他就叫B树，至于原因我觉的没必要再这个名字上纠结吧！！

        其实简单点说B树就是多叉平衡树，为什么这么说呢？其实他就是在平衡二叉树原有的基础上，进行改进的。为什么要改进呢？其实也很简单，就像我们排序的时候一样，我们不可能一直在内存中进行排序，也有可能在内存外排序，也就是外排序，这个同样的道理，就是当我们的数据多到一定程度的时候，内存中也就存不下了，而且就算存的下，也不会存，先不说大型项目中的那些数据，如果一不小把程序给关了，那么这些数据就没了，所以我们选择存储在磁盘上。但是我们在磁盘上怎么找他呢？如果我们在代码中找他的时候，那么势必要把磁盘数据加载到内存中，而我们找数据讲究的是快，所以我们采用一定的数据结构来管理这些数据，以方便我们查找的时候，可以快速的找到。

        我们学习过的数据结构中，查找能排上号的就是哈希，AVL，红黑树等。但是此时要想到一个问题就是，用这些数据结构中的其中一个来保存这些数据，那么我们势必要进行IO，这个是无可避免的，因为我们要知道的是，这个是从磁盘上读取数据到内存中。所以我们每次进行比较的时候，都是一次IO，这样就大大的降低了我们查找的效率。

如上图中的二叉树，其实我们一般存储的是文件块的地址，来一个数据，因为这里是地址，所以我们每个节点都要进行IO，所以此时就效率就低了。

也有人说用哈希，哈希其实也是一个道理，它也要进行IO。我们查找数据的时候吗，总不能拿着地址访问把，且有的时候，哈希冲突严重的时候，每个桶下面挂链表还不如挂成红黑树，此时不就又绕回来了吗？所以，此时B树就闪亮登场了。

B树的规则：

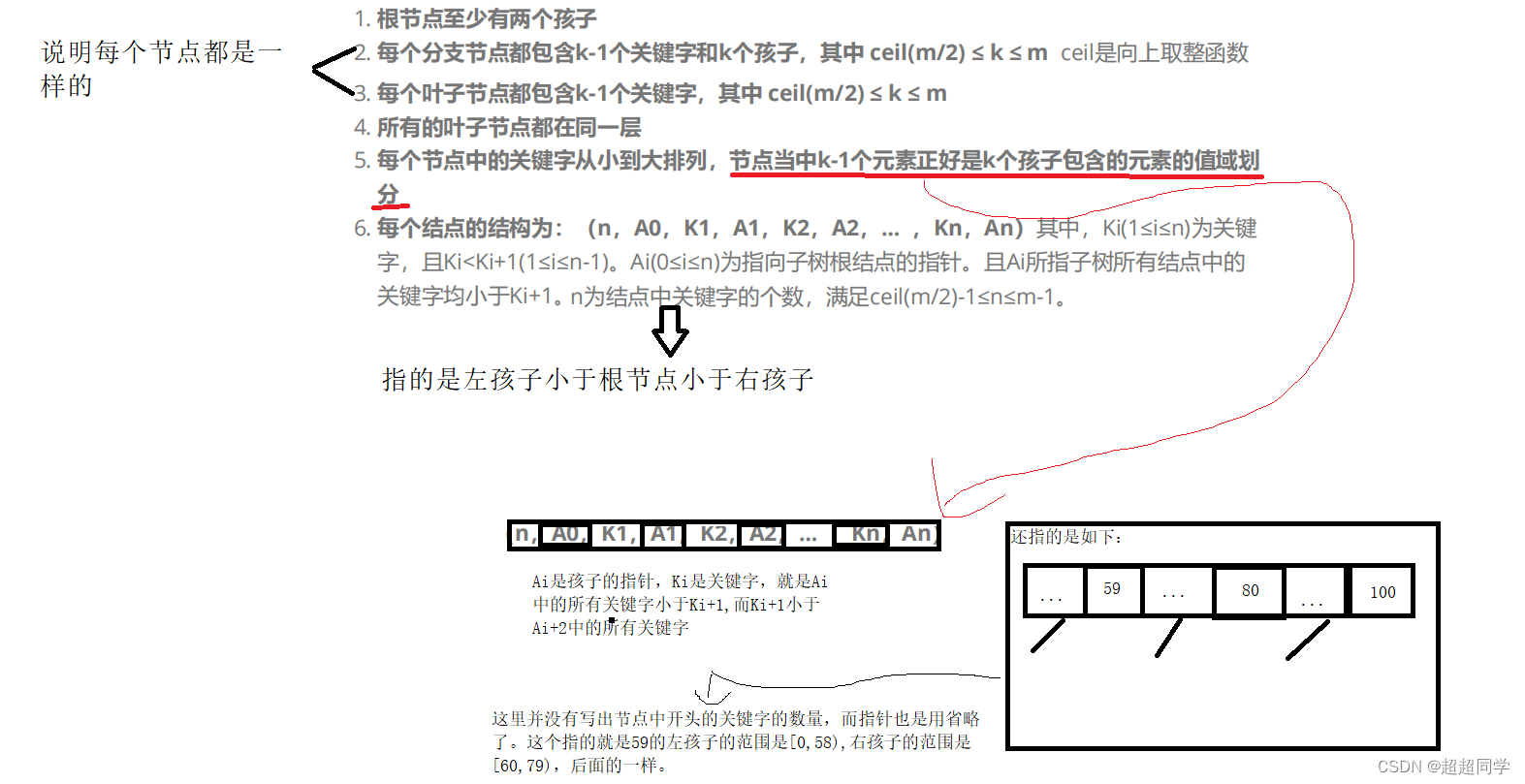规则如上，这里就不再详细说了。

好了，我们知道了B树的规则，那么我们为什么要用B树呢？其实B树是减少了IO次数。为什么呢？因为我们用B树的时候，B树的每个节点的所存储的关键字数量比AVL，红黑树等数据结构要多，所以他每次进行IO 的时候，就可以一次读取多个关键子和孩子所指向的文件数据块。这样，我们就变相的减少了IO次数。且B树的每个节点的m一般系统会设置成1024，至于为什么，深入了解过文件系统的伙伴大概知道(这里我自己也是看到过网上有人说，至于原因，个人了解的也不太清楚，好像是跟文件系统的什么大小有关来着，也是1024，知道的伙伴可以说一下)，这样就大大减少了B树的高度，最差情况下，也是进行高度次IO，而此时的IO次数最多也就是4次。所以大大提高了效率。

二、B+树

B+树在原有的B树的基础上进行了改进，就是把每个节点的孩子数量改成和关键字数量相等了。然后是每个分支节点只有索引，没有映射的值。叶子结点改成了类似于链表的形式，且叶子结点包含映射的值，并且叶子结点中包含了所有节点的索引(关键字)，并且是有序的。并且每个分支节点的第一个关键字是其对应的孩子节点的最小值。如下：

这样的改进就使得每次搜索必然是要到叶子结点，因为只有这样才可以拿到关键字所映射的内容。

而这样的话，其实是在一定程度上减少了IO次数，因为B树是每个节点都有关键字和其所映射的内容，而B+树都是关键字，所以每个节点的关键相对于B树是增加了的。也就是在相同空间下，B+树一次IO的节点数比B树一次IO的节点数要多。

其次，就是B+树的比那里遍历相对于B树来说是方便了很多。它直接可以遍历叶子结点，就可以得到所有内容。

三、B*树

其实B*树就是在B+树上做了一些相应的改进，它整体是提高了空间利用率，但是其他方面与B+树没有什么本质区别。且在运用的时候，B+树用的较多。而B*树不是没用，而是相对于B+树来说，运用的较少而已。

四、时间复杂度

其实怎么说，老师讲课的时候说的是logMN(m为底，n的对数)，但是我感觉这样有点不太对劲。后来我在网上查了些资料，有的说是mlogmn、logm*logmn，logn。其实我个人认为logmn是不对的，我自己也想了很久，其实也不能说是不对，只是这个时间复杂度是是最好的情况下是logmn，我认为我刚刚说的以上的三个是比较正确的(logmn只是个人感觉不太对，不是错的，就是这个是最好的情况以下，才是logmn)。

1.m*logmn

因为我们都知道的是，B树的每个节点都是有M-1个关键字，这里1影响不大，所以直接省略。那么最坏的情况下是每个节点都比较得到最后一个节点，比较B树的高度次，所以就应该是m*logmn。有些伙伴说这里可以把m给省略了，就是logmn，但是我想说的是，这里不可以省略。因为将近十亿个数据的高度是将近3-4层，也就是3<=logmn<=4,而系统默认给的B树的每个节点m=1024,所以这里m的影响还是很大的，所以我认为是不可以省略的。而其实这里的时间复杂度也是跟m的取值有关。如果m取值相对于logmn的影响较小，此时才可以省略。如果就用系统默认给的m，这里我认为是不可以省略的。

2.logm*logmn

这个就很好理解了，因为每个节点的关键字都是有序的，所以我们在查找每个节点的关键字的时候，不要遍历，只需要直接用二分查找就好，所以是logm*logmn。

后面的一个是logn其实就是二分查找这个方法的时间复杂度化简得到的。这里简单说一下，就是用换底公式就可以化简出来。

五、Mysql与B树系列

其实学习过数据库的都知道，数据库本质是管理文件中的数据，而数据结构是管理内存中的数据。那么，我们B树系列的数据结构与数据库有什么关系呢？其实也很容易就也可以想到。因为B树系列的诞生使得我们可以进行在磁盘上进行查找数据时大大提高了效率。但是，特闷到底是什么关系呢？

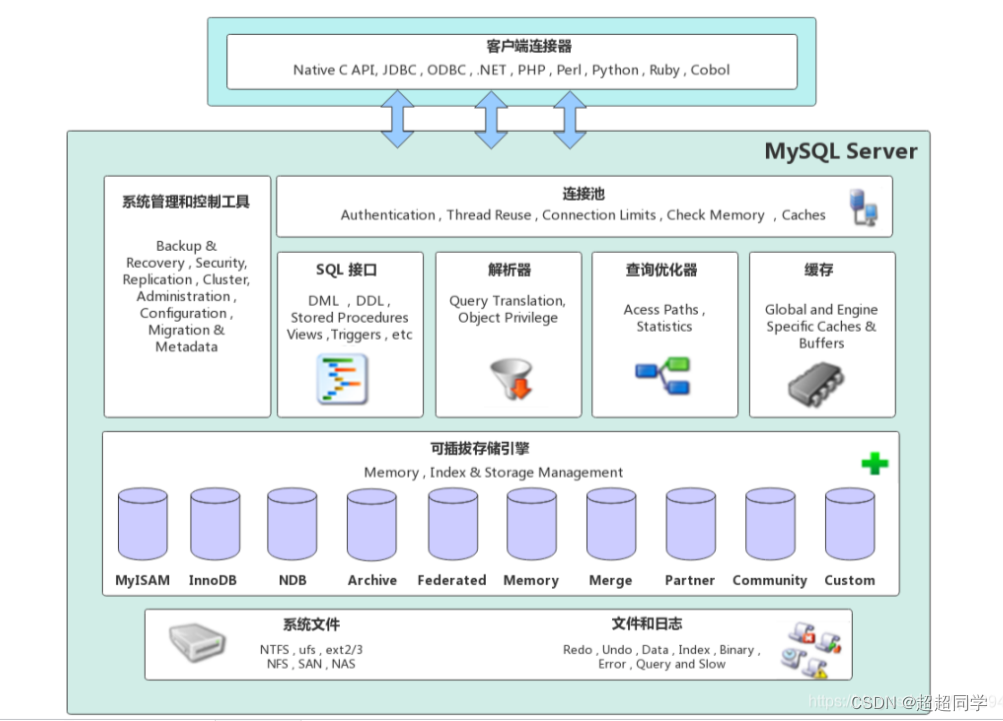
其实Mysql本质就是cs模型，这里就不详细说明。建立数据库其实本质上就是在存储引擎的这里建立B+树。然后存储引擎下面就是文件系统。而其实缓存就是把磁盘数据加载到缓存中。就是类似于LRU这种缓存。而这里主要说一下两种搜索引擎

1.MyISAM

其建立的B+树是索引文件与数据文件分开的。索引在我理解来说就是B+树种的关键字。再用SQL语句建立表的时候，一般都会有个主键，主键是唯一的。(这里是数据库的知识)，而B+树建立的时候，其key就是这个主键，叶子结点是会挂一个val的值来对应映射。如果想用其他搜索，只需建立索引就可以。建立索引数据库重新建立一个B+树，然后把这个索引当成key。

2.InnoDB

其建立的B+树是索引文件与数据文件不分离的，也就是在一起的。注意的是，这个搜索引擎建立索引的B+树的时候，其叶子结点的val是主键值。

Mysql这里讲的比较浅，如果有伙伴想了解的，也可以私信，可以互相探讨一下。过几天会发B树系列的代码实现，到时候也会详细说数据库与B树系列的关系。有了代码就好理解了。

最后，希望大家支持一下，谢谢！！！！