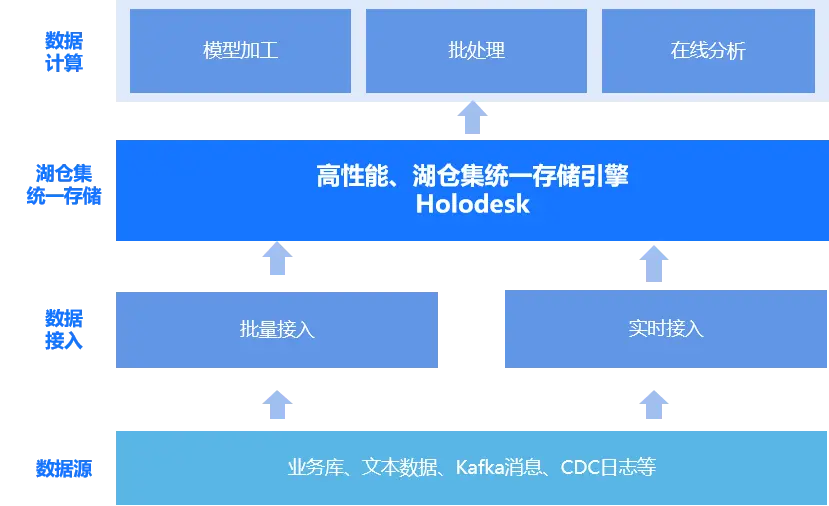
CSP-202112-3-登机牌条码
解题思路
一、.处理大小写和数字
-
初始化变量:
flag: 用来标识当前处理的字符类型,0代表大写字母,1代表小写字母,2代表数字。 -
大小写字母和数字的处理:
- 小写字母(
'a' <= it && it <= 'z'):如果之前处理的字符不是小写字母(flag != 1),则在inputData中加入数字27,表示从其他类型字符切换到小写字母。然后,根据smallMode映射表,将当前字符转换成相应的数字并加入到inputData中。最后,将flag设置为1,表示当前正在处理小写字母。 - 大写字母(
'A' <= it && it <= 'Z'):如果之前处理的字符不是大写字母(flag != 0),则在inputData中加入数字28,表示从其他类型字符切换到大写字母。如果之前是处理小写字母(flag == 1),还需要再次加入28,以确保大小写之间的明确分界。然后,根据bigMode映射表,将当前字符转换成相应的数字并加入到inputData中。设置flag为0,表示当前正在处理大写字母。 - 数字(
'0' <= it && it <= '9'):如果之前处理的字符不是数字(flag != 2),则在inputData中加入数字28,表示从其他类型字符切换到数字。然后,根据numMode映射表,将当前字符转换成相应的数字并加入到inputData中。最后,将flag设置为2,表示当前正在处理数字。
- 小写字母(
二、inputData长度偶数化
if (inputData.size() % 2 == 1) inputData.push_back(29);
三、inputData转化为码字
codeNum.push_back(0); // 第一个码字空出记录长度
for (int i = 0; i < inputData.size(); i += 2)
{
int num = 30 * inputData[i] + inputData[i + 1];
codeNum.push_back(num);
}
四、计算长度
-
校验级别设定:根据
s的值决定校验码k的长度。如果s不等于-1(意味着需要一定级别的错误检测或纠正),k将被设置为2的s + 1次幂;否则不需要进行差错码的计算int k = s != -1 ? pow(2, s + 1) : 0; -
长度检查和填充:
-
检查当前的码字序列长度加上校验码长度后,是否能被
w整除,其中w是预设的编码块的长度。如果总长度正好是w的倍数,那么不需要添加任何填充,且将codeNum序列的第一个元素(通常用于存放长度信息)设置为codeNum的长度。 -
如果总长度不是
w的倍数,则计算需要填充的数量fillNum,这个数字等于w减去codeNum.size() + k除以w的余数。然后,将codeNum序列的第一个元素设置为原长度加上填充数量。 -
接下来,通过循环将值为900的填充码添加到
codeNum序列中,直到填充数量满足要求。这里,数字900通常用作填充数据,这是一种约定,可能因具体应用而有所不同。
if ((codeNum.size() + k) % w == 0) { codeNum[0] = codeNum.size(); } else { int fillNum = w - ((codeNum.size() + k) % w); codeNum[0] = codeNum.size() + fillNum; for (int i = 0; i < fillNum; i++) { codeNum.push_back(900); } } -
五、校验码计算(难点)
1. 计算生成多项式 g(x):
g[0] = 1;
int a = -3;
for (int i = 1; i <= k; a = a * 3 % mod, i++)
{
for (int j = i - 1; j >= 0; j--)
{
g[j + 1] = (g[j + 1] + g[j] * a) % mod;
}
}
g[0] = 1;初始化生成多项式g(x),其中最低次项(常数项)被设置为1。- 通过两层循环构造生成多项式。外层循环控制多项式的次数,即
k。内层循环用于计算多项式的每个系数。在每次外循环迭代中,a以3的幂递增,并在模mod下进行。 - 内层循环更新多项式的系数。对于每个新的
i,它实质上是在多项式中加入一个新的项。这个过程不仅依赖当前的系数g[j],而且还依赖于该系数与a的乘积。g[j] * a:多项式系数的更新。g[j]表示生成多项式g(x)当前的第j项系数。将这个系数乘以ag[j + 1] + g[j] * a:把g[j] * a的结果加到下一个系数g[j + 1]上。这样做的目的是调整和形成下一个系数的值。
2. 初始化d(x)(深拷贝)
d[0] = codeNum[0];
for (int i = 1; i < codeNum.size(); i++)
{
d[i] = codeNum[i];
}
3. 使用g(x)计算d(x)的余数:
for (int i = 0; i < codeNum.size(); i++)
{
int x = d[i];
d[i] = 0;
for (int j = 1; j <= k; j++)
{
d[i + j] = (d[i + j] - x * g[j]) % mod;
}
}
d(x)被用来计算与g(x)相除的余数。这个过程类似于长除法,其中d(x)被逐步修改为新的值,这些值表示除法的中间和最终结果。x是当前考虑的d(x)的系数,而g(x)的系数则用于计算d(x)的新系数。这个过程是多项式除法的关键步骤,并且是生成校验码的核心。
4. 输出校验码:
for (int i = codeNum.size(); i < codeNum.size() + k; i++)
{
cout << (-d[i] % mod + mod) % mod << endl;
}
完整代码
#include <iostream>
#include <vector>
#include <unordered_map>
#include <algorithm>
#include <cmath>
#include <deque>
using namespace std;
const int mod = 929, N = 1e5 + 10;
vector<int>g(N), d(N);
unordered_map<char, int> bigMode{
{'A', 0}, {'B', 1}, {'C', 2}, {'D', 3}, {'E', 4},
{'F', 5}, {'G', 6}, {'H', 7}, {'I', 8}, {'J', 9},
{'K', 10}, {'L', 11}, {'M', 12}, {'N', 13}, {'O', 14},
{'P', 15}, {'Q', 16}, {'R', 17}, {'S', 18}, {'T', 19},
{'U', 20}, {'V', 21}, {'W', 22}, {'X', 23}, {'Y', 24},
{'Z', 25}
};
unordered_map<char, int> smallMode{
{'a', 0}, {'b', 1}, {'c', 2}, {'d', 3}, {'e', 4},
{'f', 5}, {'g', 6}, {'h', 7}, {'i', 8}, {'j', 9},
{'k', 10}, {'l', 11}, {'m', 12}, {'n', 13}, {'o', 14},
{'p', 15}, {'q', 16}, {'r', 17}, {'s', 18}, {'t', 19},
{'u', 20}, {'v', 21}, {'w', 22}, {'x', 23}, {'y', 24},
{'z', 25}
};
unordered_map<char, int> numMode{
{'0', 0}, {'1', 1}, {'2', 2}, {'3', 3}, {'4', 4},
{'5', 5}, {'6', 6}, {'7', 7}, {'8', 8}, {'9', 9}
};
int main() {
int w, s;
cin >> w >> s;
string inputString;
cin >> inputString;
// 1.处理大小写和数字
vector<int>inputData;
vector<int>codeNum;
int flag = 0; // 大写-0 小写-1 数字-2
for (auto& it : inputString) {
if (it >= 'a' && it <= 'z') {
if (flag != 1) inputData.push_back(27);
inputData.push_back(smallMode[it]);
flag = 1;
}
else if (it >= 'A' && it <= 'Z') {
if (flag != 0) {
inputData.push_back(28);
if (flag == 1) inputData.push_back(28);
}
inputData.push_back(bigMode[it]);
flag = 0;
}
else if (it >= '0' && it <= '9') {
if (flag != 2) inputData.push_back(28);
inputData.push_back(numMode[it]);
flag = 2;
}
}
// 2.inputData长度偶数化
if (inputData.size() % 2 == 1) inputData.push_back(29);
// 3.inputData变成码字
codeNum.push_back(0); // 第一个码字空出记录长度
for (int i = 0; i < inputData.size(); i += 2)
{
int num = 30 * inputData[i] + inputData[i + 1];
codeNum.push_back(num);
}
// 4.计算长度
int k = s != -1 ? pow(2, s + 1) : 0;
if ((codeNum.size() + k) % w == 0)
{
codeNum[0] = codeNum.size();
}
else
{
int fillNum = w - ((codeNum.size() + k) % w);
codeNum[0] = codeNum.size() + fillNum;
for (int i = 0; i < fillNum; i++)
{
codeNum.push_back(900);
}
}
// 打印输出
for (const auto& it : codeNum) cout << it << endl;
// 计算校验码
if (s != -1)
{
//计算g(x)
g[0] = 1;
int a = -3;
for (int i = 1; i <= k; a = a * 3 % mod, i++)
{
for (int j = i - 1; j >= 0; j--)
{
g[j + 1] = (g[j + 1] + g[j] * a) % mod;
}
}
//计算d(x)
d[0] = codeNum[0];
for (int i = 1; i < codeNum.size(); i++)
{
d[i] = codeNum[i];
}
for (int i = 0; i < codeNum.size(); i++)
{
int x = d[i];
d[i] = 0;
for (int j = 1; j <= k; j++)
{
d[i + j] = (d[i + j] - x * g[j]) % mod;//关键代码,建议自己实际模拟一次
}
}
for (int i = codeNum.size(); i < codeNum.size() + k; i++)
{
cout << (-d[i] % mod + mod) % mod << endl;//取反后输出,注意要取模时要加上mod
}
}
return 0;
}