一、选择

下列与队列结构有关联的是（）

A 函数的递归调用
B 数组元素的引用
C 多重循环的执行
D 先到先服务的作业调度

下面关于abstract关键字描述错误的是（）

A abstract关键字可以修饰类或方法
B final类的方法都不能是abstract，因为final类不能有子类
C abstract类不能实例化
D abstract类的子类必须实现其超类的所有abstract方法

结构化程序的三种基本结构是（）

A 递归、迭代和回溯
B 过程、函数和子程序
C 顺序、选择和循环
D 调用、返回和选择

下面选项中,哪些是interface中合法方法定义?()

A public void main(String [] args);
B private int getSum();
C boolean setFlag(Boolean [] test);
D public float get(int x);

下面哪些类实现或继承了 Collection 接口？（）

A HashMap
B ArrayList
C Vector
D Iterator

二、编程

1. 计算糖果

计算糖果
A,B,C三个人是好朋友,每个人手里都有一些糖果,我们不知道他们每个人手上具体有多少个糖果,但是我们知道以下的信息：
A - B, B - C, A + B, B + C. 这四个数值.每个字母代表每个人所拥有的糖果数.
现在需要通过这四个数值计算出每个人手里有多少个糖果,即A,B,C。这里保证最多只有一组整数A,B,C满足所有题设条件。

2. 进制转换

进制转换
给定一个十进制数M，以及需要转换的进制数N。将十进制数M转化为N进制数。

答案

1. 选择

队列：先进先出 原则。

故：选D

① abstract 可以修饰类or方法
② 抽象类不能实例化
③ 抽象方法不能被private修饰，默认是public
④ 抽象方法不能被final和static修饰，因为抽象方法要被子类重写
⑤ 抽象类必须被继承，并且继承后子类要重写父类中的抽象方法，否则子类也是抽象类，必须要使用 abstract 修饰。（也就是子类也是抽象类就可以不重写父类抽象方法）
⑥ 抽象类可以含有抽象方法，不含也ok；但是含有抽象方法的类一定是抽象类。
⑦ 抽象类可以实现接口。

参考：abstract

故：选D

结构化程序的三种结构是：顺序、选择和循环。

故：选C

① 接口中每一个方法都是public的抽象方法, 即接口中的方法会被隐式的指定为 public abstract（只能是 public abstract，其他修饰符都会报错）
② 即：接口中的方法要么是显式地public修饰，要么是省略（默认public abstract修饰）
③ 接口中的方法都是抽象方法，都没有方法体。

故：选ACD

Map、Collection、Iterator、Comparable、Arrays

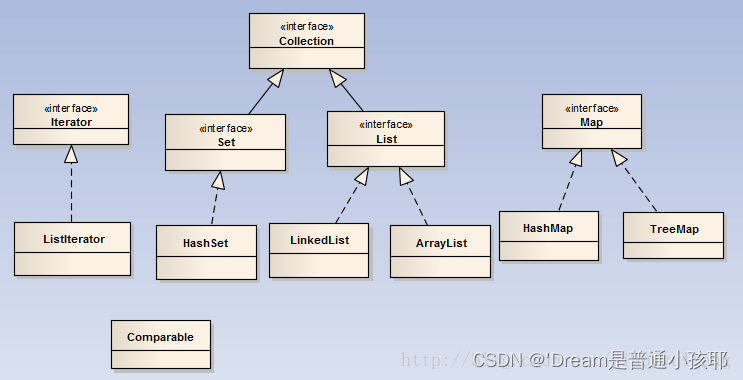
参考：集合框架

故：选BC

程序包含算法，算法就是程序的灵魂，一个需要实现特定功能的程序，实现它的算法可以有很多种，所以算法的优劣决定着程序的好坏。

2. 编程

计算糖果
1）思路：
① 根据所给的 A - B, B - C, A + B, B + C 四个表达式来计算A、B、C三个值，也就是三元一次求解。

① A = ((A-B）+（A+B)) / 2;
② B1 = ((B-C) + (B+C)) / 2；
③ C = ((B+C) - (B-C)) / 2;
④ B2 = ((A+B) - (A-B)) / 2;

② 判断是否有解：B1 = B2？

2）代码：


import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 输入： A - B，B - C，A + B，B + C
        int a = in.nextInt();
        int b = in.nextInt();
        int c = in.nextInt();
        int d = in.nextInt();

        // 首先计算A、C
        int A = (a+c)/2;
        int C = (d-b)/2;
        // 在计算B1、B2
        int B1 = (b+d)/2;
        int B2 = (c-a)/2;

        //判断是否有解
        if(B1 == B2) {
            // 有解
            System.out.println(A + " " + B1 + " " + C);
        } else {
            System.out.println("No");
        }

    }
}

进制转换
1）思路：

① N进制转为十进制：x1 * N⁰ + x2 * N¹ + …
② 十进制转N进制：[除N倒余法] 数%N=x, 数=数/N，…一直到数/N==0 停止。（倒余就是结果）

2）为了方便拼接，先使用可变字符串存结果；完成后要进行reverse反转字符串操作（倒余操作）。

3）注意：当进制>10时，一定要注意转为字母！！（可以写一个字符串对照着取！！）

代码：

import java.util.Scanner;

public class Main {
     public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int m = in.nextInt();
        int n = in.nextInt();
        boolean flg = false;  // 判断是否是负数
        String table = "0123456789ABCDEF"; // 十六进制对照表
        StringBuilder ret = new StringBuilder(); // 最终转换结果

        // 开始进行转换
        if(m < 0) { // 负数
            m = -m;
            flg = true;
        }
         // 这儿，说明此时m>=0!

        if(m == 0) { // 单独判断0
            ret.append('0');
        }
        while(m != 0) {
            // 这里是可能出现字母的，此时就对照着table进行取！！
            ret.append(table.charAt(m%n));
            m = m/n;
        }
        // 判断负数加符号就行
        if(flg == true) {
            ret.append('-');
        }

        // 进行倒余操作
        ret.reverse();
        // 输出就行
        System.out.println(ret.toString());
    }
}