1、引入

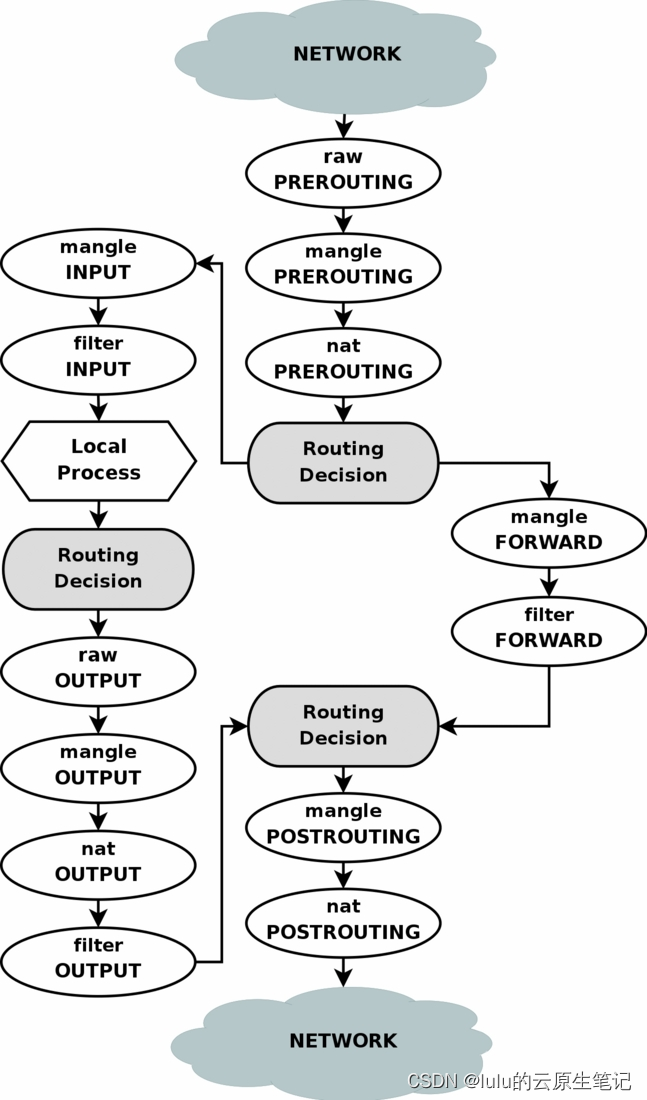
线段树解决的是 区间查询 和 区间更新 的问题， $O (l o g n)$ 复杂度。

人为规定：数组下标从 1 开始。

如果要计算数组某个范围 L 到 R 的累加和，那么可以准备一个前缀和数组 help，得到前缀和数组后，可以 $O (1)$ 复杂度快速求出 L 到 R 的累加和。

如原数组 arr = [5, 3, 2, 4, 9, 0, 1]，则 help = [5, 8, 10, 14, 23, 23, 24]，如果要计算下标 3 ~ 5 的值的累加和，直接用 help[5] - help[2] = 15，求解速度非常快。但是这种求解数组某个范围的累加和的方法是基于原数组 arr 不再变化的前提。

如果原数组中的某个数修改了值，那么 help 数组就存在需要大量更新的问题。

那么对于原数组中的值可能变化的情况，但是还能查询范围上的累加和，需要换个结构。即该结构同时满足以下两个方法：
1）update(i, v)：将 i 位置的值修改为 v；
2）sum[L...R]：计算 L 到 R 范围的累加和。

这个结构就是 Index Tree，上述的两个方法线段树可以完美实现，但是 Index Tree 有比线段树更优的地方。

Index Tree 没法像线段树一样做到范围更新，只能单点更新后执行范围累加和的查询，这两个方法都快。

2、Index Tree 的特点

支持区间查询
没有线段树那么强，但是非常容易改成一维、二维、三维的结构
只支持单点更新

3、Index Tree讲解

原始数组 arr：[3， 1， -2， 3， 6， 0， 9]
	   下标： 1   2   3   4   5   6  7

准备一个 help 数组（相同长度的配成一对）
1）1位置的3长度为1，前面没有长度为1的可以与之组成一对，于是就拷贝自己的值 help[1] = arr[1] = 3 (长度为1)
2）2位置的1长度为1，前面有长度为1的3可以与之组成一对，于是 help[2] = arr[1] + arr[2] = 4 （长度为2）
3）3位置的-2长度为1，前面没有长度为1的可以与之组成一对，于是拷贝自己的值 help[3] = arr[3] = -2 (长度为1）
4）4位置的3长度为1，前面有长度为1的-2可以与之组成一对，二者相加 = 1，此时已经长度为2，而前面又有长度为2的可以与之组成一对，于是 help[4] = arr[1] + arr[2] + arr[3] + arr[4] = 5 (长度为4）
5）5位置的6长度为1，附近前面没有长度为1的，于是 help[5] = arr[5] = 6 (长度为1）
6）6位置的0长度为1，前面长度为1的6可以与之组成一对，help[6] = arr[5] + arr[6] = 6 (长度为2）
7）7位置的9长度为1，前面没有长度为1的可以与之组成一对，于是help[7] = arr[7] = 9 （长度为1）

抛开数组中的值，仅看 help 数组每个元素管理的原数组的下标：
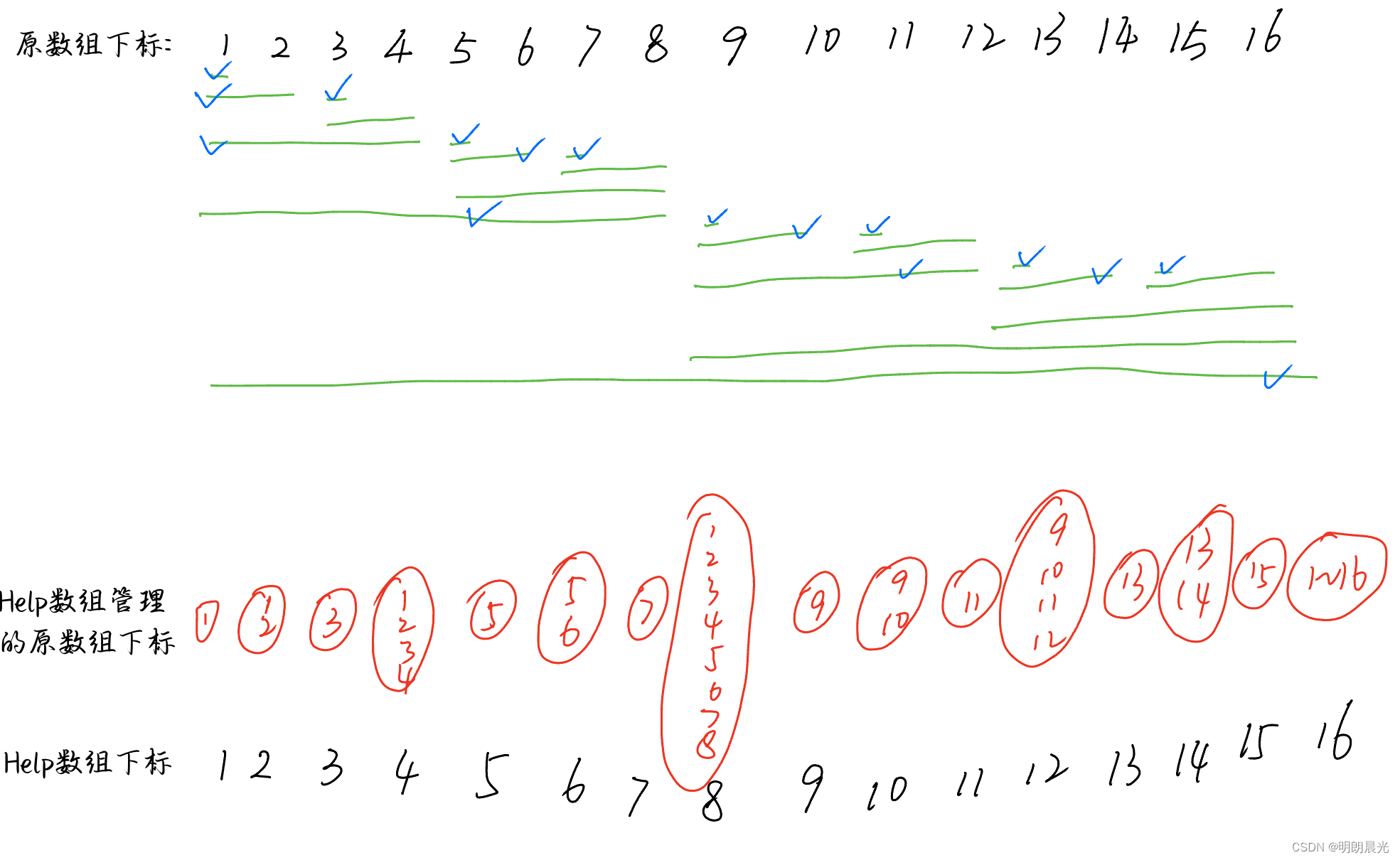
请添加图片描述
即 相同长度进行合并。

【规律1 ：help 数组的 index 管理的是 index 的二进制形式中的从右往左的第一个1拆开后加1到它自己这个范围的数】

例如 index = 010111000，那么它管理的是原数组中的 010110001 ~ 010111000 这个范围的值，即将 index 中从右往左数的第一个1拆开后加1到它自己的范围。

例原数组 arr 下标从 1 到 8，那么help数组中的 index = 8 的位置管理的是原数组1到8范围的值，即 8 = 01000，拆开1加1 = 00001，所以管理的范围为 00001 ~ 01000 就是 1~8 范围。

同理 index = 12时，12 = 01100，第一个1去掉后加1 = 01001，所以管理的范围是 01001 ~ 01100，即原数组的9 ~ 12范围。

【利用help数组求原数组中1 ~ $i$ 位置的前缀和】

例1：求原数组1 ~ 33 范围的前缀和，33 的二进制形式是0100001，那么就是help数组中 33 这个位置的值 a，以及将33的二进制形式的最后一个1去掉得到的0100000，对应到help数组中的该位置的 b，将help数组中的这两个位置的值相加即是原数组 1 ~ 33 这个范围的前缀和。为什么正确呢？因为help数组中的 33 就管理原数组的33位置的数，而help数组中的32 位置管理1 ~ 32 位置的数，所以二者相加就是1 ~ 33 范围的和。

例2：求原数组 1 ~ $i$ 范围的前缀和，其中 $i = 0101100110$ ，那么就是取出 help 数组的如下位置的值进行累加：

help[0101100110] = a，拿出help数组中 $i$ 位置的数
help[0101100100] = b，在上一步的基础上抹掉一个1
help[0101100000] = c，在上一步的基础上抹掉一个1
help[0101000000] = d，在上一步的基础上抹掉一个1
help[0100000000] = e，在上一步的基础上抹掉一个1
直到没有 1 可以抹掉，即index = 0 为止。

所以 sum[1...i] = a + b + c + d + e

为什么这个流程正确呢？

当 $i = 0110100$ 时，在上述流程中取的是 help 数组中的：

help[0110100]，管理的是原数组的 arr[0110001] ~ arr[0110100]

help[0110000]，管理的是原数组的 arr[0100001] ~ arr[0110000]

help[0100000]，管理的是原数组的 arr[0000001] ~ arr[0100000]

可见，管理的原数组的范围全部是连续的，所以就正确得到了原数组 1 ~ $i$ 的前缀和。

4、代码实现

public class IndexTree {

	// 下标从1开始！
	public static class IndexTree {

		private int[] tree;
		private int N;

		// 0位置弃而不用！
		public IndexTree(int size) {
			N = size;
			tree = new int[N + 1];
		}
		// 根据index的位信息处理的，index的二进制位中有多少个1就需要操作多少次，得到每位的信息就是每次右移1位，即除以2
		// 所以时间复杂度 O(logn)
		// 函数功能：求1~index范围的累加和
		// 所以如果要求 L 到 R的累加和 = 1~R的累加和 - 1~L-1的累加和
		public int sum(int index) { 
			int ret = 0;
			while (index > 0) {
				ret += tree[index];
				index -= index & -index; //去掉最右侧的1
			}
			return ret;
		}

		// index & -index : 提取出index最右侧的1出来
		// index :           0011001000
		// index & -index :  0000001000
		// x & (-x) = x & (~x + 1) 
		public void add(int index, int d) {  //时间复杂度 O(logn)
			//认为原始数组一开始全部为0，现在要给index位置的数加d，那么tree数组（即help数组）就会有位置的数受到影响
			//比如原数组的 3 位置的数发生了变化，那么 tree 数组中的哪些位置会受牵连呢？
			// 3 的二进制为011，将最右侧的1加1 = 100，即4
			// 4 = 100 最右侧的1 加1 = 1000，即8
			// 8 = 1000 最右侧的1 加1 = 10000，即16
			// 即 011 -> 100 -> 1000 -> 10000 ->.... 
			//规律：只需要将发生更新位置的值的二进制的最右侧1加1 就能得到它影响tree数组哪些位置的值
			while (index <= N) {
				tree[index] += d; //当前位置+d
				index += index & -index; //最右侧的1加1，找出受到牵连的位置
			}
		}
	}
	
	//暴力解
	public static class Right {
		private int[] nums;
		private int N;

		public Right(int size) {
			N = size + 1;
			nums = new int[N + 1];
		}

		public int sum(int index) {
			int ret = 0;
			for (int i = 1; i <= index; i++) {
				ret += nums[i];
			}
			return ret;
		}

		public void add(int index, int d) {
			nums[index] += d;
		}

	}

	public static void main(String[] args) {
		int N = 100;
		int V = 100;
		int testTime = 2000000;
		IndexTree tree = new IndexTree(N);
		Right test = new Right(N);
		System.out.println("test begin");
		for (int i = 0; i < testTime; i++) {
			int index = (int) (Math.random() * N) + 1;
			if (Math.random() <= 0.5) {
				int add = (int) (Math.random() * V);
				tree.add(index, add);
				test.add(index, add);
			} else {
				if (tree.sum(index) != test.sum(index)) {
					System.out.println("Oops!");
				}
			}
		}
		System.out.println("test finish");
	}
}