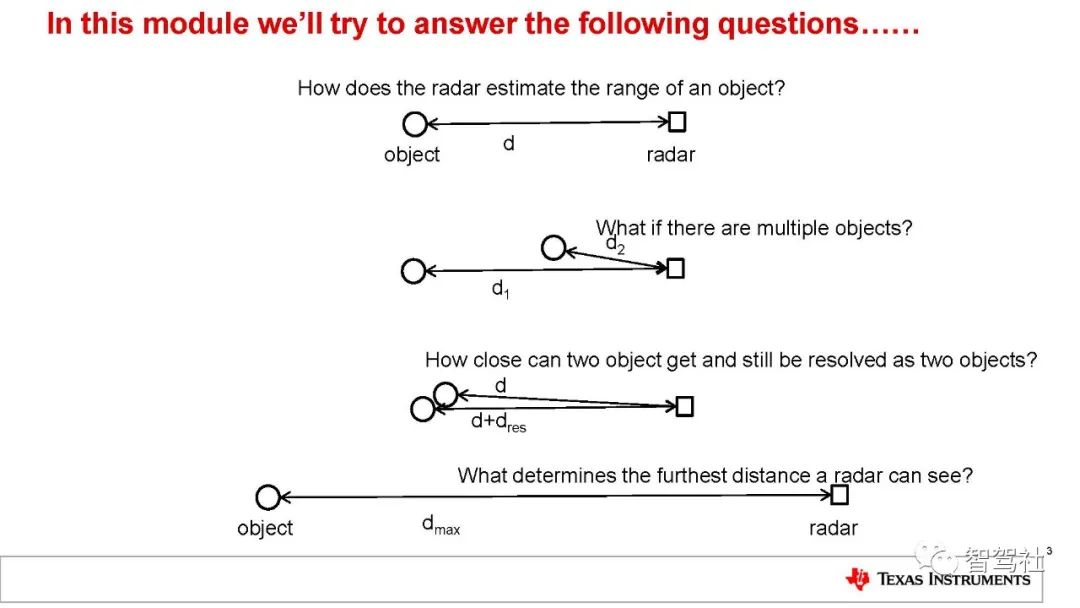
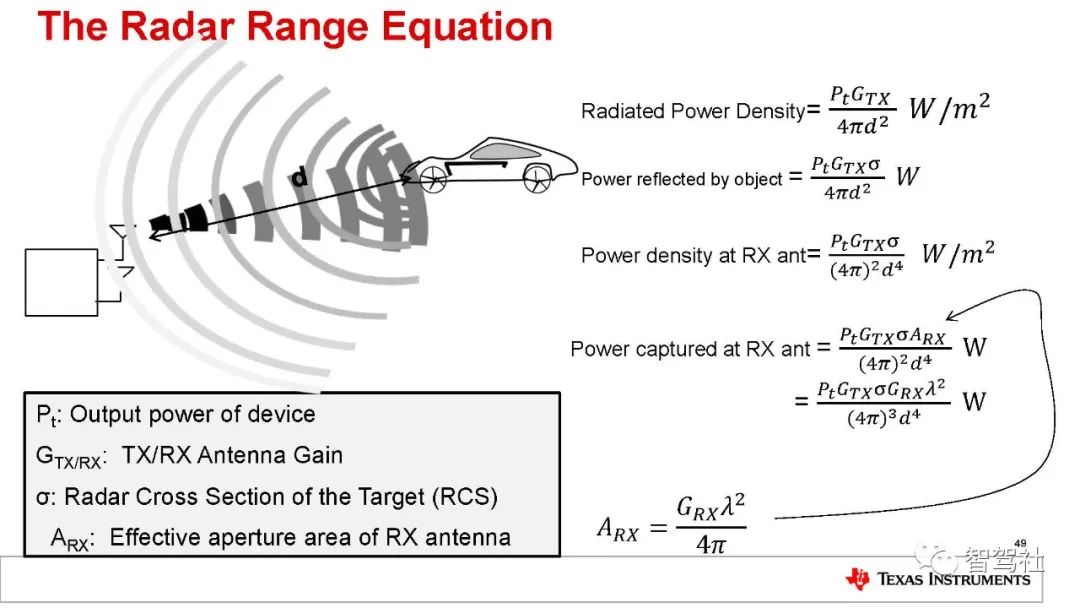
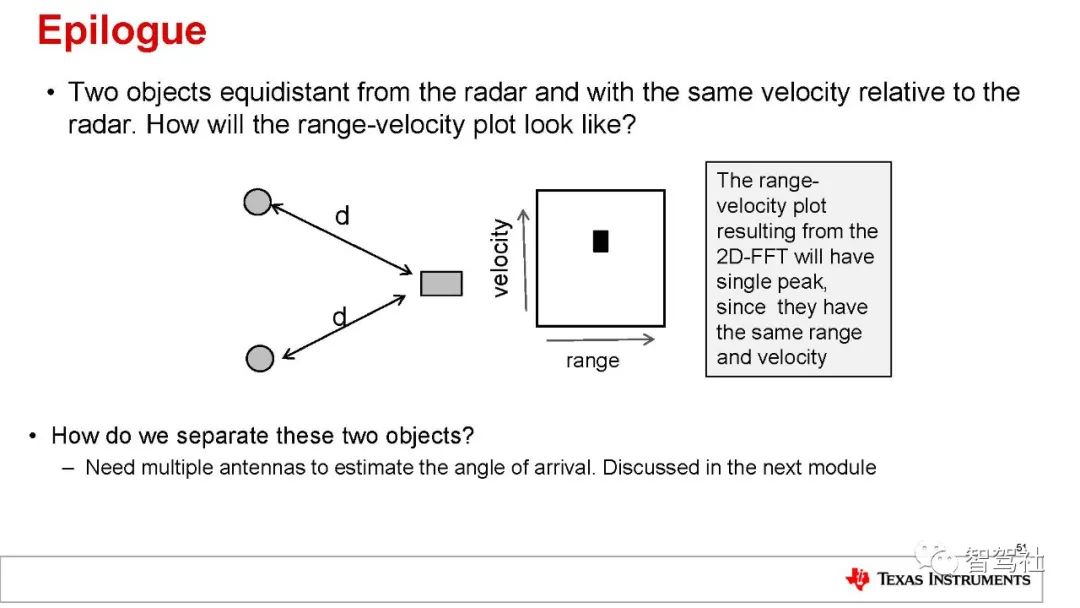
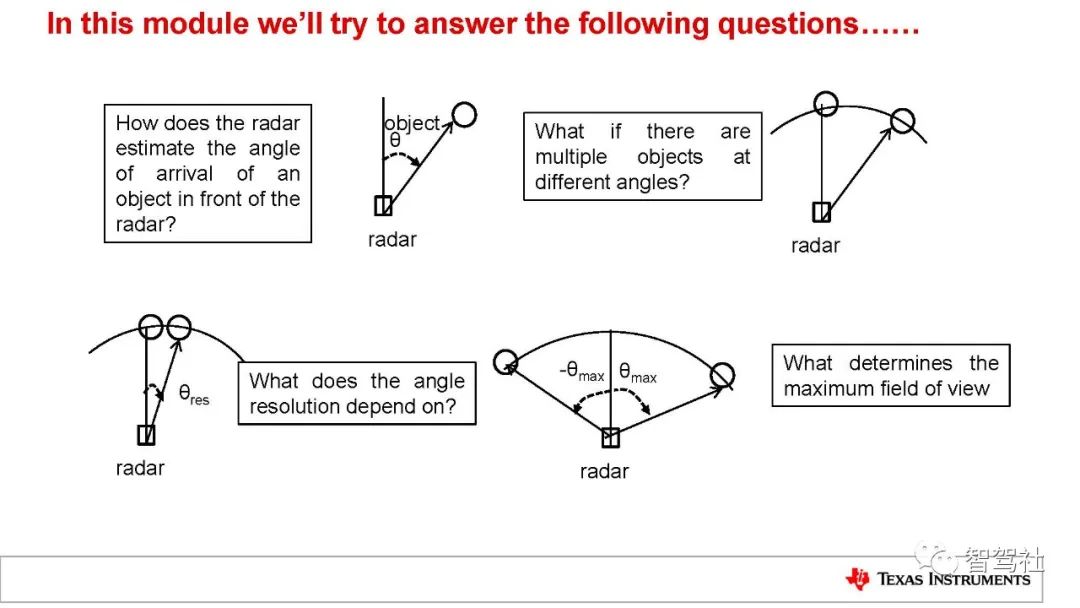
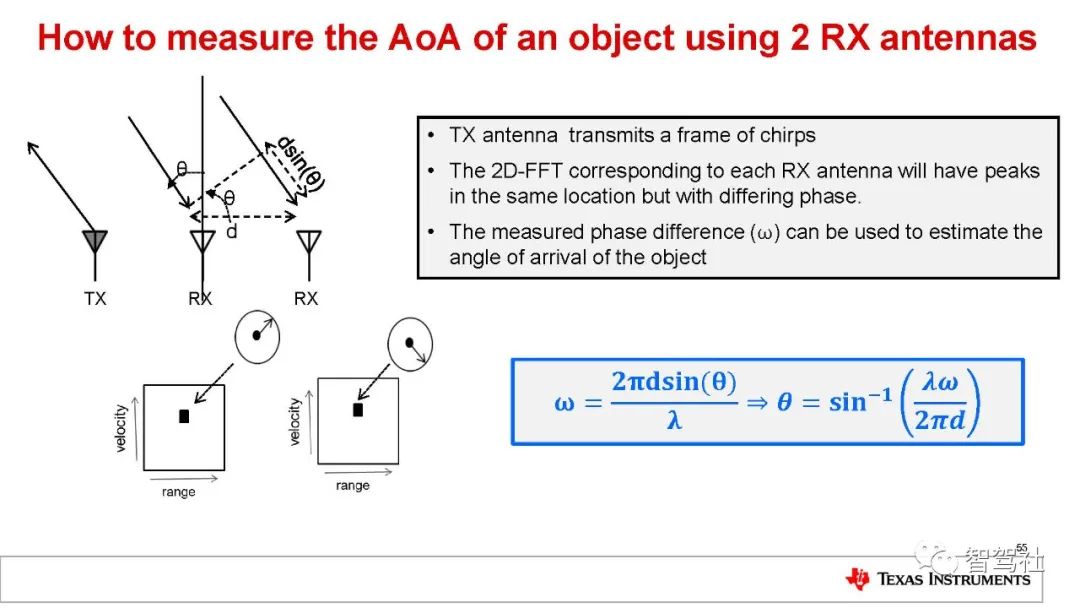
毫米波 (mmWave) 是一类使用短波长电磁波的特殊雷达技术。雷达系统发射的电磁波信号被其发射路径上的物体阻挡继而会发生反射。通过捕捉反射的信号，雷达系统可以确定物体的距离、速度和角度。

毫米波雷达可发射波长为毫米量级的信号。在电磁频谱中，这种波长被视为短波长，也是该技术的优势之一。诚然，处理毫米波信号所需的系统组件（如天线）的尺寸确实很小。短波长的另一项优势是高准确度。工作频率为 76–81GHz（对应波长约为 4mm）的毫米波系统将能够检测小至零点几毫米的移动。

完整的毫米波雷达系统包括发送 (TX)和接收 (RX)射频 (RF)组件，以及时钟等模拟组件，还有模数转换器 (ADC)、微控制器 (MCU) 和数字信号处理器 (DSP) 等数字组件。过去，这些系统都是通过分立式组件实现的，这增加了功耗和总体系统成本。其复杂性和高频率要求使得系统设计颇具挑战性。 

德州仪器 (TI) 已经克服了这些挑战，并且设计出了基于互补金属氧化物半导体 (CMOS) 的毫米波雷达器件，该器件集成了时钟等 TX-RF 和 RX-RF 组件，以及ADC、MCU 和硬件加速器等数字组件。TI的毫米波传感器产品组合中的某些系列集成了 DSP，用于提供额外的信号处理功能。

TI 器件可实现一种称为调频连续波 (FMCW) 的特殊毫米波技术。顾名思义，FMCW 雷达连续发射调频信号，以测量距离以及角度和速度。这与周期性发射短脉冲的传统脉冲雷达系统不同。

距离测量

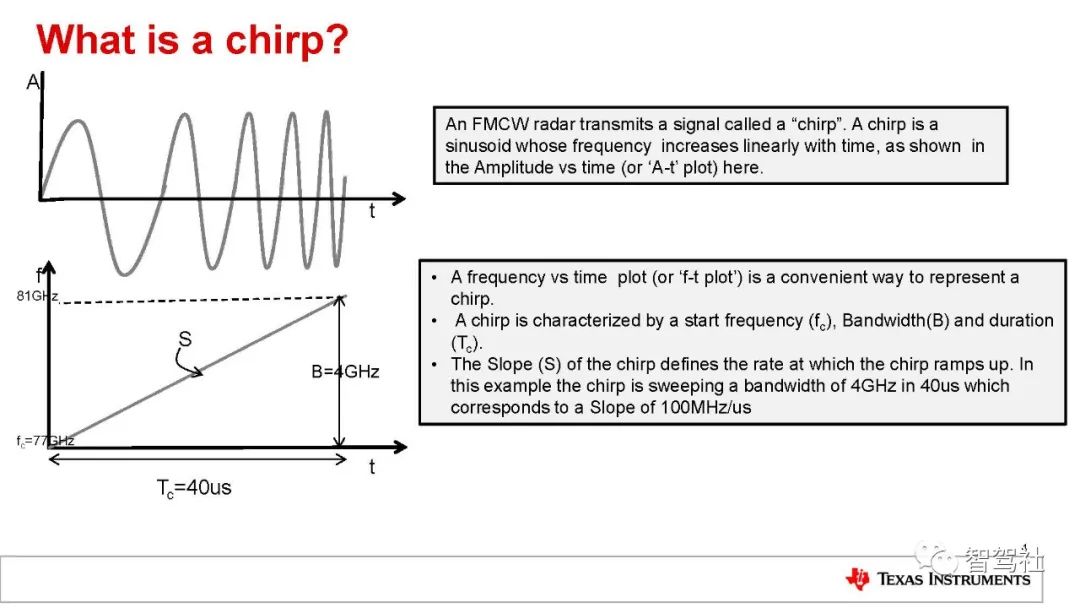
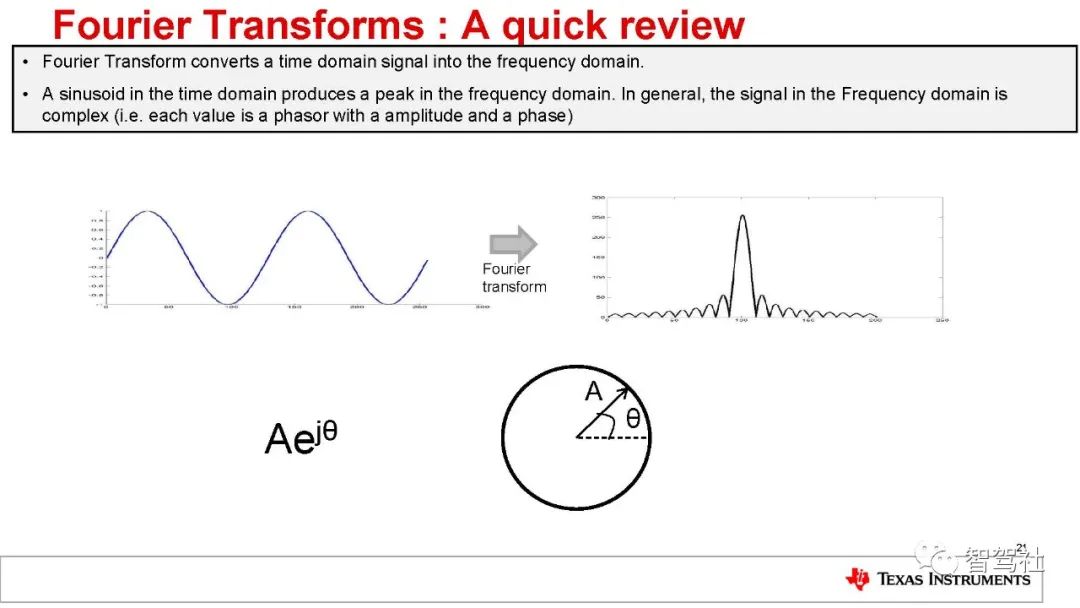
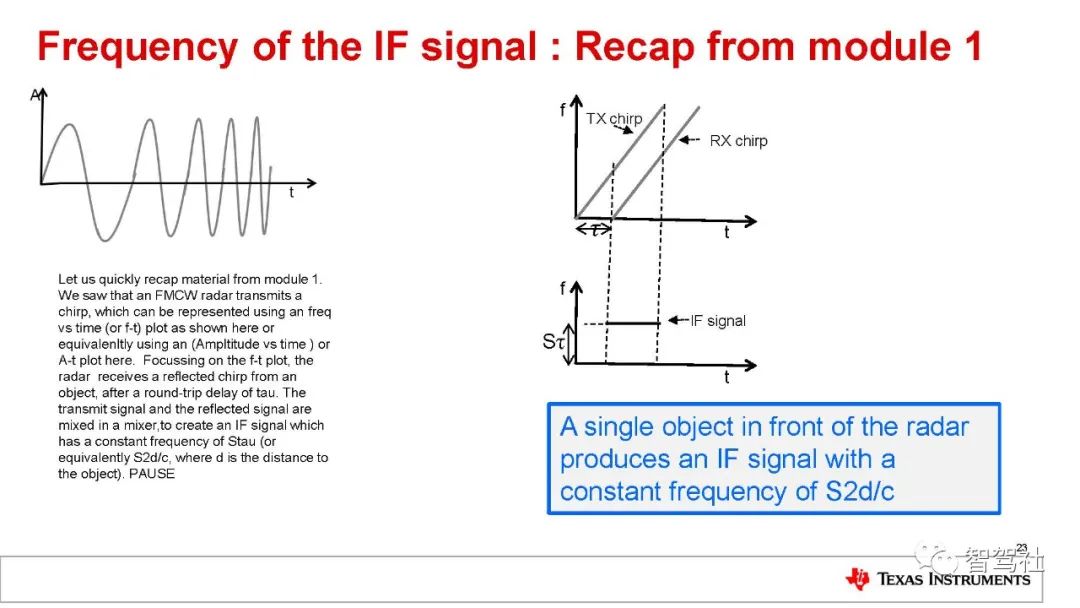
在雷达系统中，其基本概念是指电磁信号发射过程中被其发射路径上的物体阻挡进行的反射。FMCW 雷达系统所用信号的频率随时间变化呈线性升高。这种类型的信号也称为线性调频脉冲。图 1 以幅度（振幅）相对时间的函数，显示了线性调频脉冲信号表示。

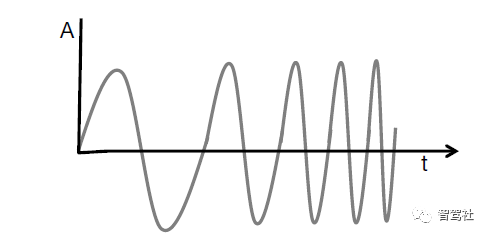
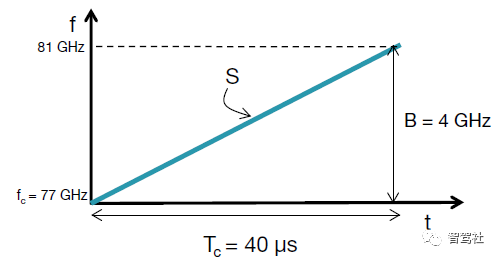
图 2为同一个线性调频脉冲信号（频率作为时间的函数）。该线性调频脉冲具有起始频率 (fc)、带宽(B)和持续时间 (Tc)。该线性调频脉冲的斜率 (S)捕捉频率的变化率。在例子中图 2 提供的示例中，fc = 77 GHz，B = 4 GHz，Tc = 40 µs，S = 100 MHz/µs.

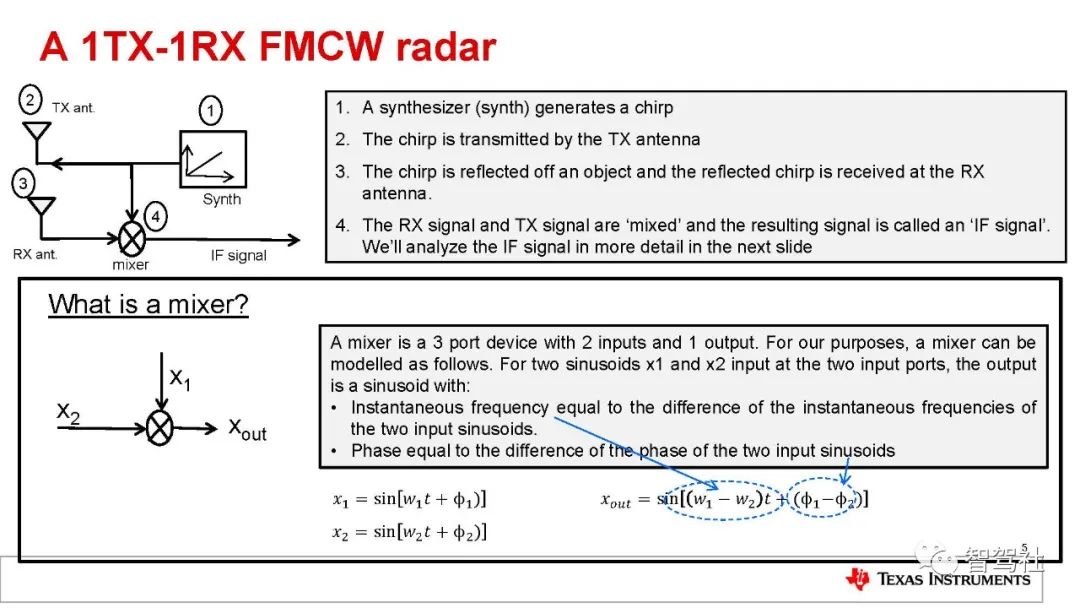
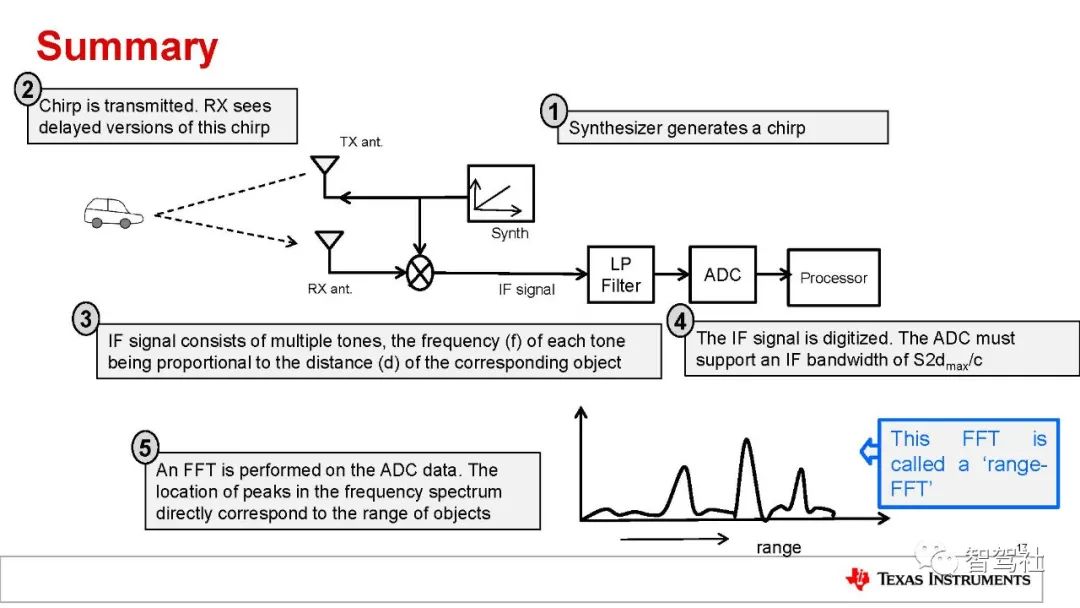
FMCW 雷达系统发射线性调频脉冲信号，并捕捉其发射路径中的物体反射的信号。图 3 所示为 FMCW 雷达主射频组件的简化框图。该雷达的工作原理如下：

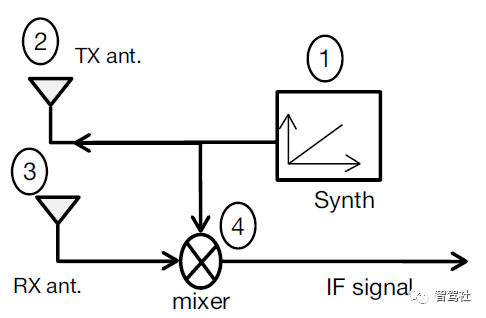
•      合成器生成一个线性调频脉冲。

•      该线性调频脉冲由发射天线（TX 天线）发射。

•     物体对该线性调频脉冲的反射生成一个由接收天线（RX天线）捕捉的反射线性调频脉冲。

•     “混频器”将 RX和TX信号合并到一起，生成一个中频 (IF)信号。

混频器是一个电子组件，将两个信号合并到一起生成一个具有新频率的新信号。

对于两个正弦输入 x1 和 x2（方程式1 和 2）

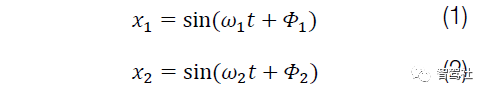
输出 xout 有一个瞬时频率，等于两个输入正弦函数的瞬时频率之差。输出xout 的相位等于两个输入信号的相位之差（方程式 3）

混频器的运行方式还可以以图形方式，通过观察作为时间函数的 TX 和 RX 线性调频脉冲频率表示法来加以理解。

下页图 4  中的上图为针对检测到的单个物体的TX和 RX线性调频脉冲作为时间的函数。请注意，该RX线性调频脉冲是 TX线性调频脉冲的延时版本。

延时(t)可通过数学方法推导出方程式4：

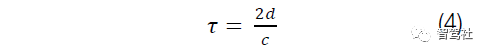
其中 d 是与被检测物体的距离，c 是光速。

要获取混频器输出处作为 IF 信号时间函数的频率表示法，只要去掉图 4上半部分中显示的两条线即可。这两条线之间的距离是固定的，这表示IF信号包含一个频率恒定的单音信号。图 4显示该频率为St。IF 信号仅在 TX 线性调频脉冲和 RX 线性调频脉冲重叠的时段（即图 4 中垂直虚线之间的时段） 有效。

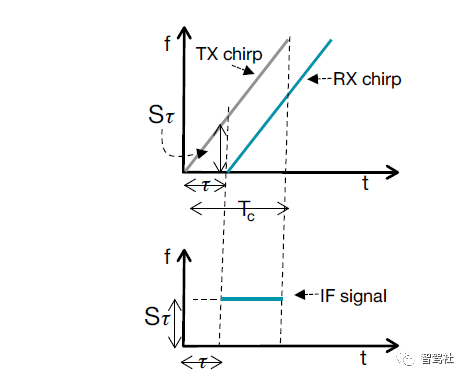
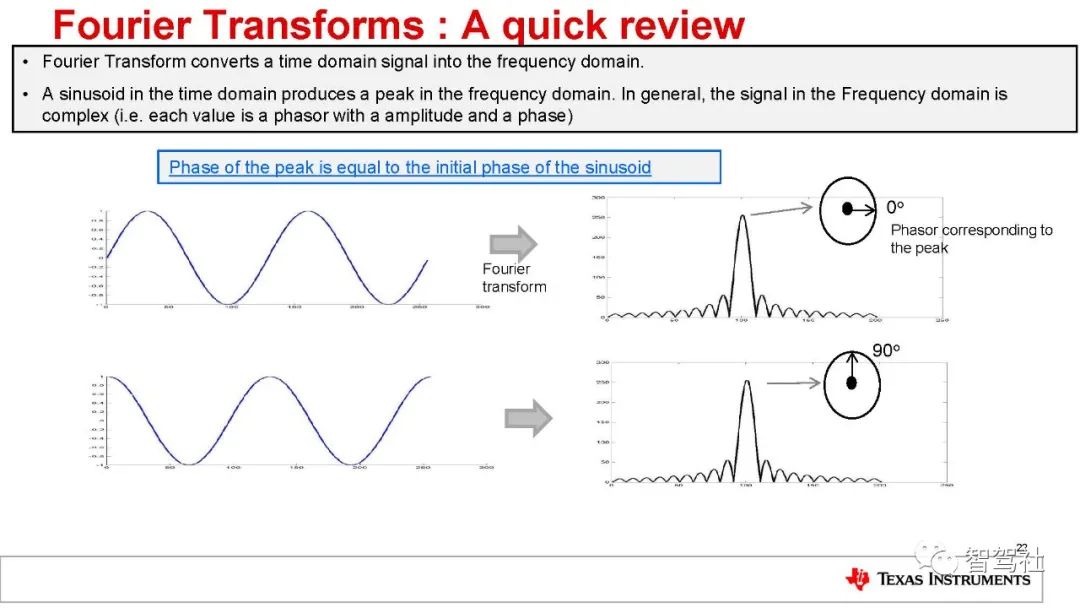
混频器输出信号作为时间的幅度函数是一个正弦波，因为它有恒定频率。

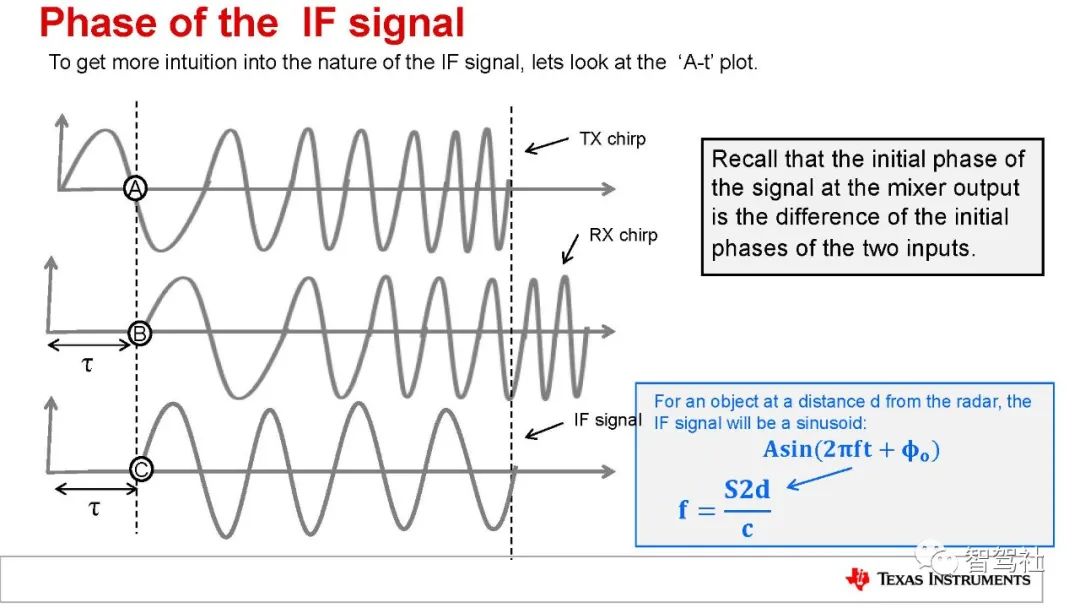
IF 信号的初始相位 (F0) 是 IF 信号起点对应的时间点（即图 4 中左侧垂直虚线表示的时间点）的 TX线性调频脉冲相位与 RX  线性调频脉冲相位之差。

（方程式 5）：

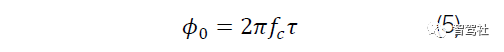
通过数学方法，它可以进一步导入方程式6：

总之，对于与雷达的距离为 d 的物体，IF 信号将是一个正弦波（方程式7），因此：

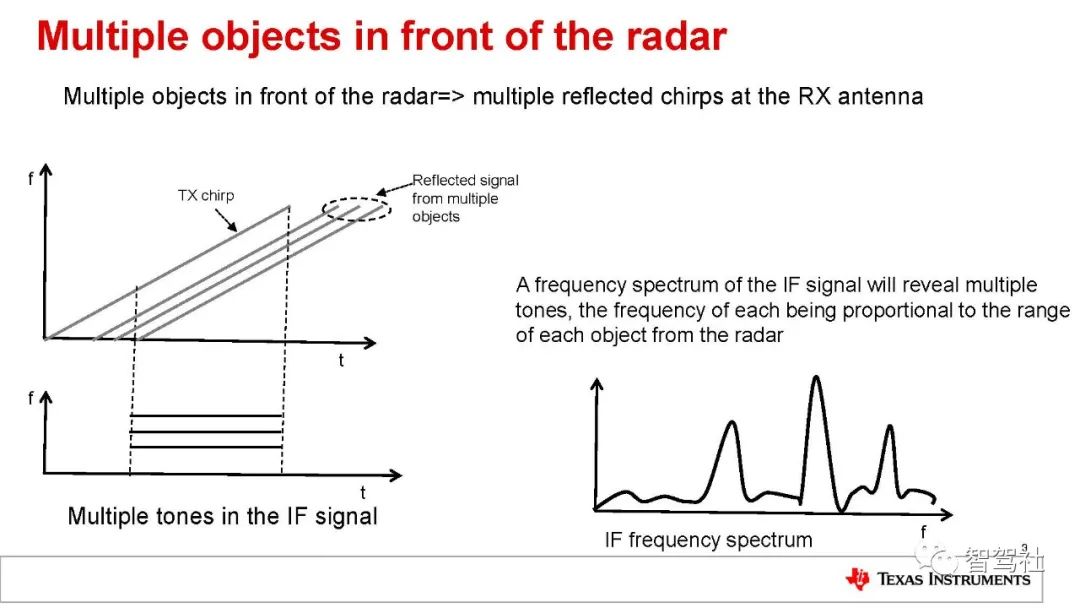
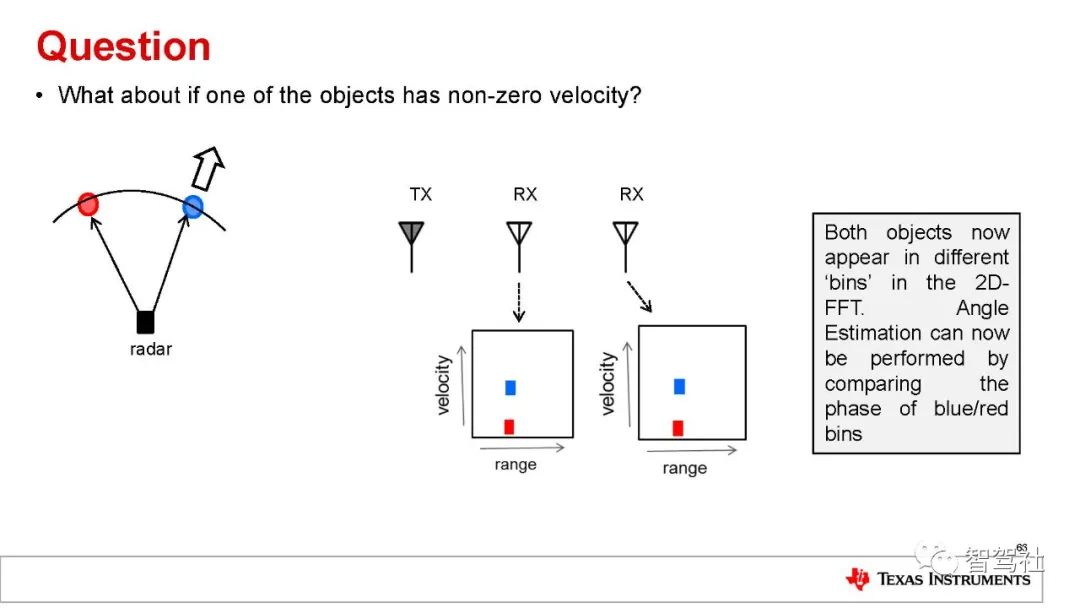
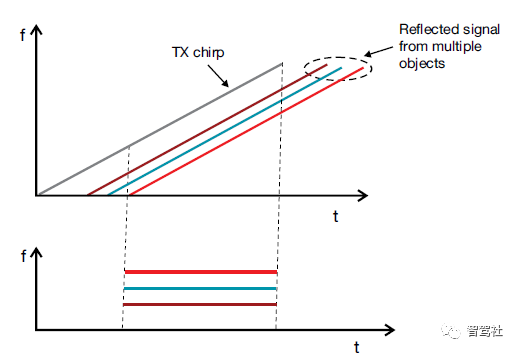
在本介绍中，我们忽略 IF  信号的频率与物体速度的依赖关系。在快速 FMCW雷达中，其影响通常非常小，且在处理完成多普勒 FFT后，即可轻松对其进行进一步校正。上述分析均假设雷达仅检测到一个物体。让我们来分析一个检测到若干物体的情形。图 5显示了接收自不同物体的三个不同的 RX  线性调频脉冲。每个线性调频脉冲的延时都不一样，延时和与该物体的距离成正比。不同的

RX 线性调频脉冲转化为多个 IF 单音信号，每个信号频率恒定。

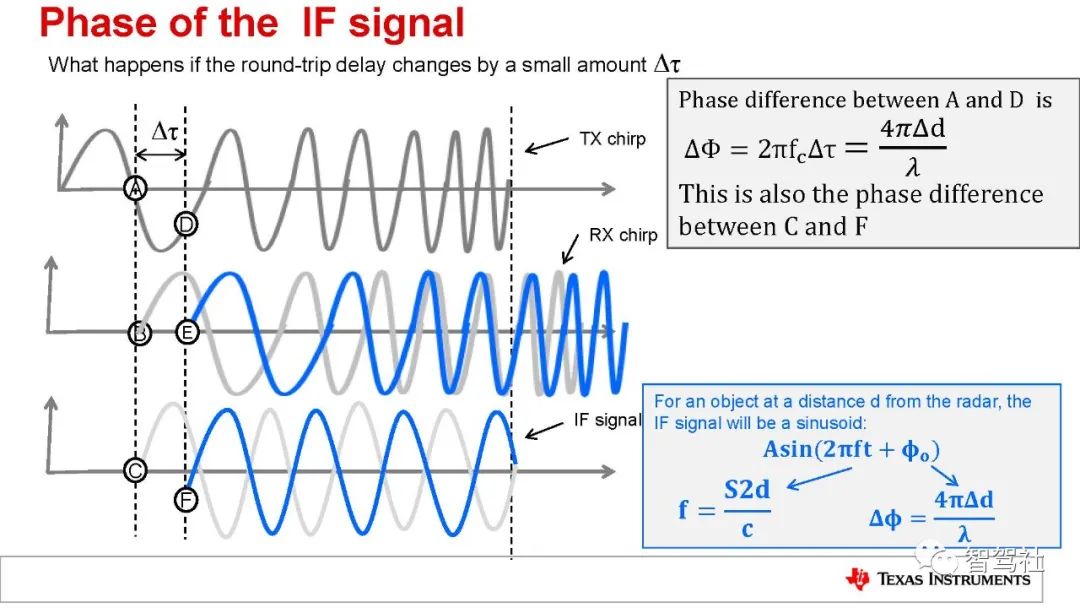
该方程式是一个近似等式，仅在斜率和距离足够小时才有效。不过，IF 信号的相位与很小的距离变化呈线性关系（即Δf=4πΔd/l）仍然是正确的。

** 在本介绍中，我们忽略 IF 信号的频率与物体速度的依赖关系。在快速 FMCW 雷达中，其影响通常非常小，且在处理完成多普勒 FFT 后，即可轻松对其进行进一步校正。

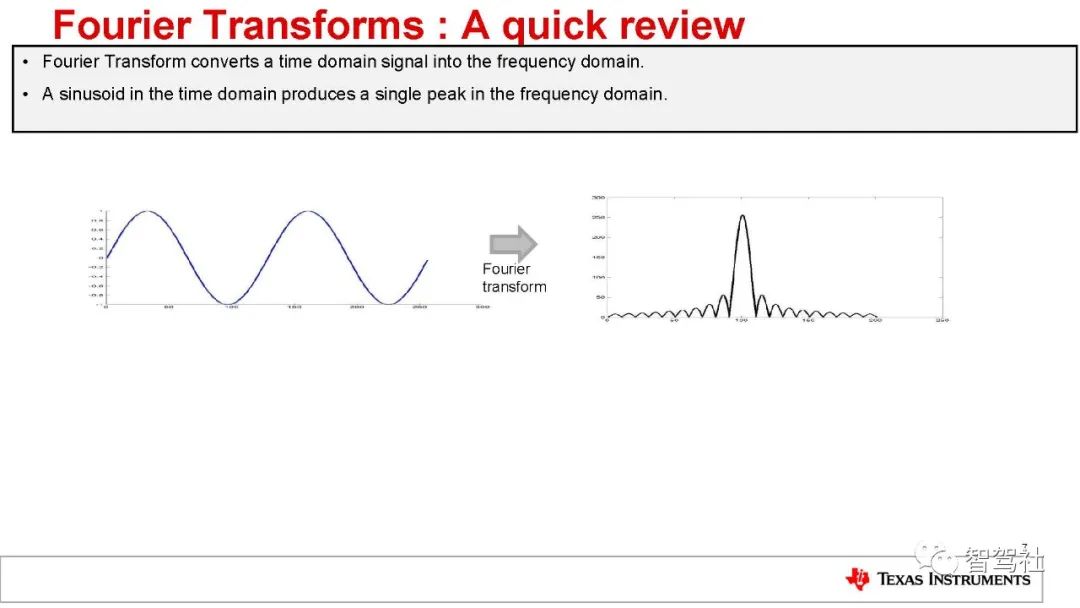
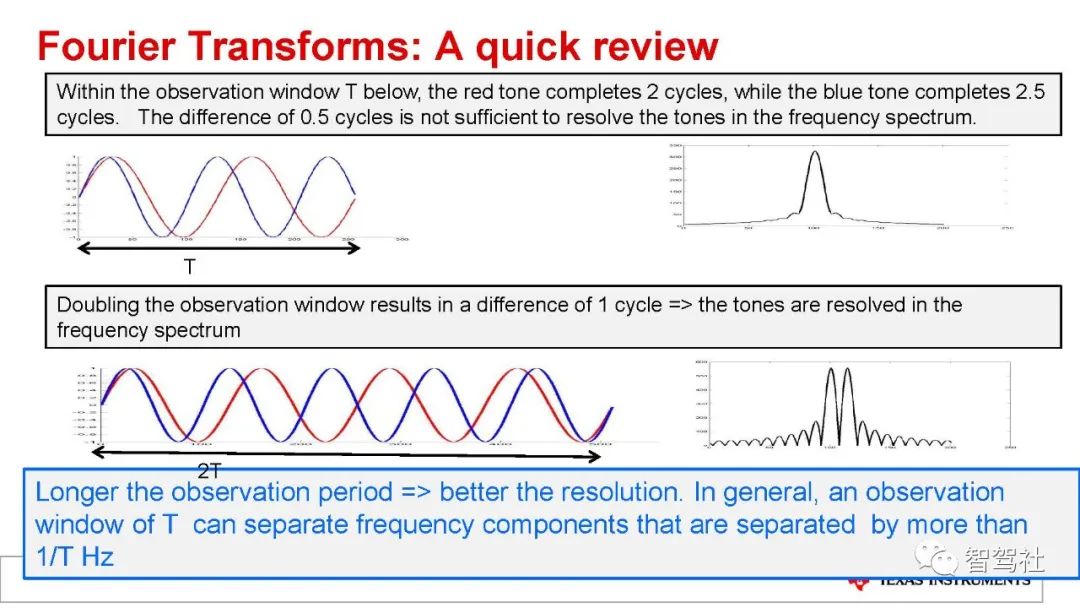
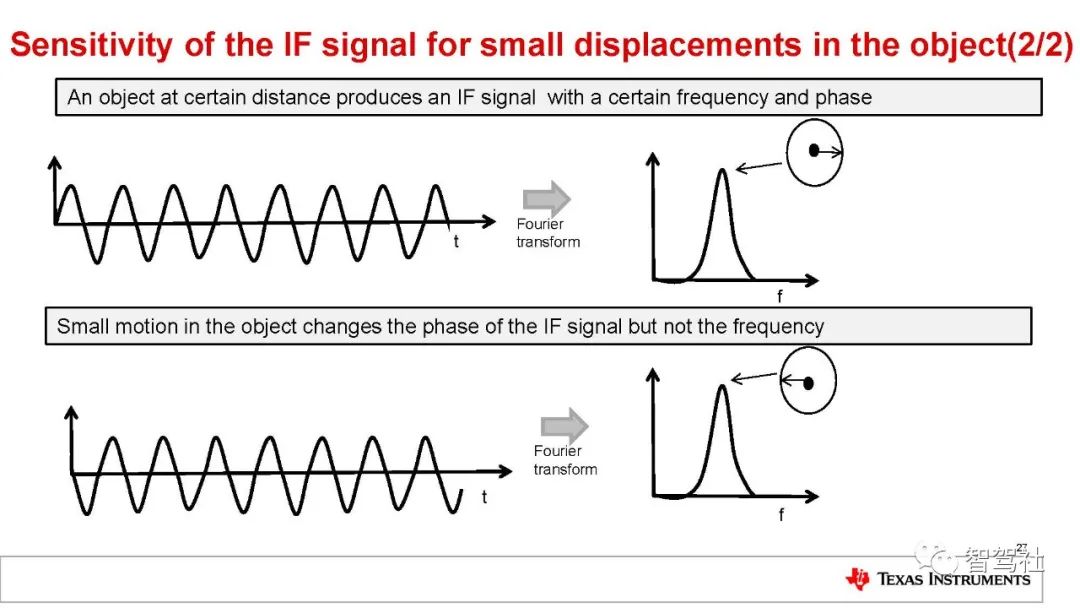
这个包含多个单音信号的 IF 信号必须使用傅里叶变换加以处理，以便分离不同的-单音。傅里叶变换处理将会产生一个具有不同的分离峰值的频谱，每个峰值表示在特定距离处存在物体。

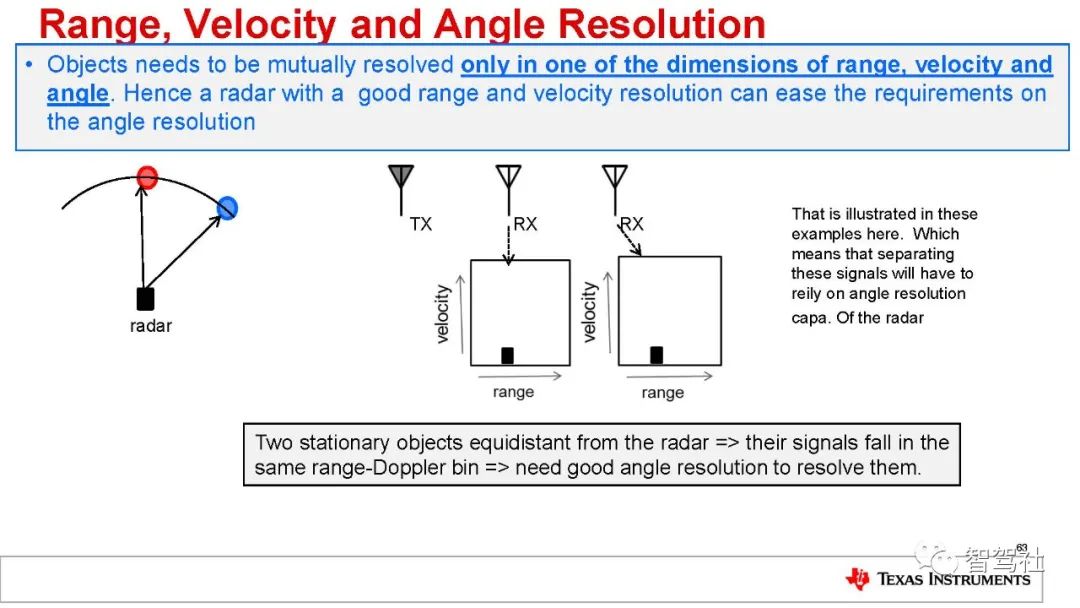
距离分辨率

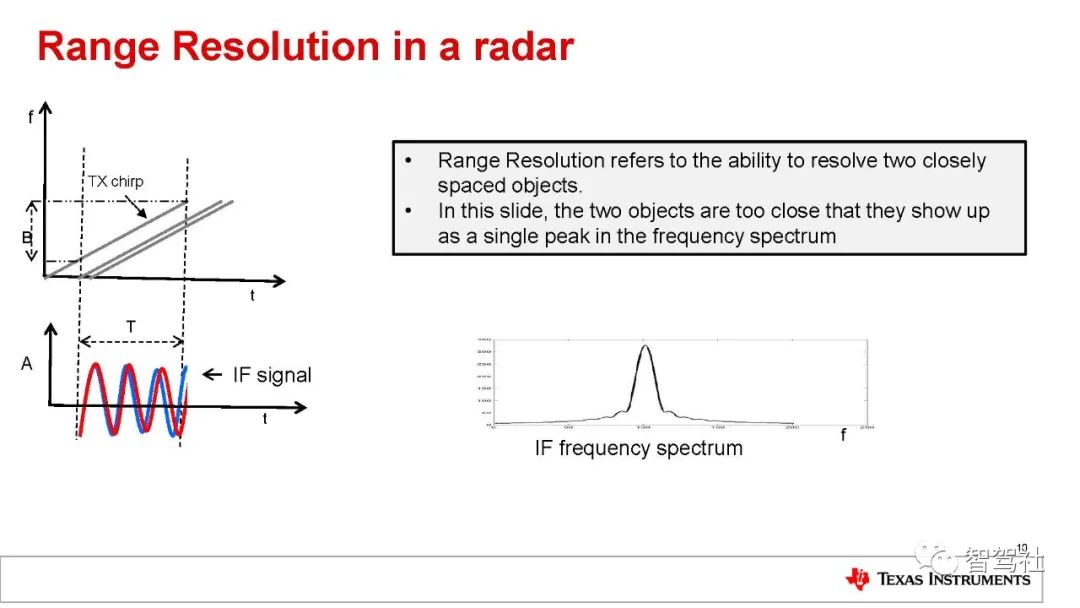
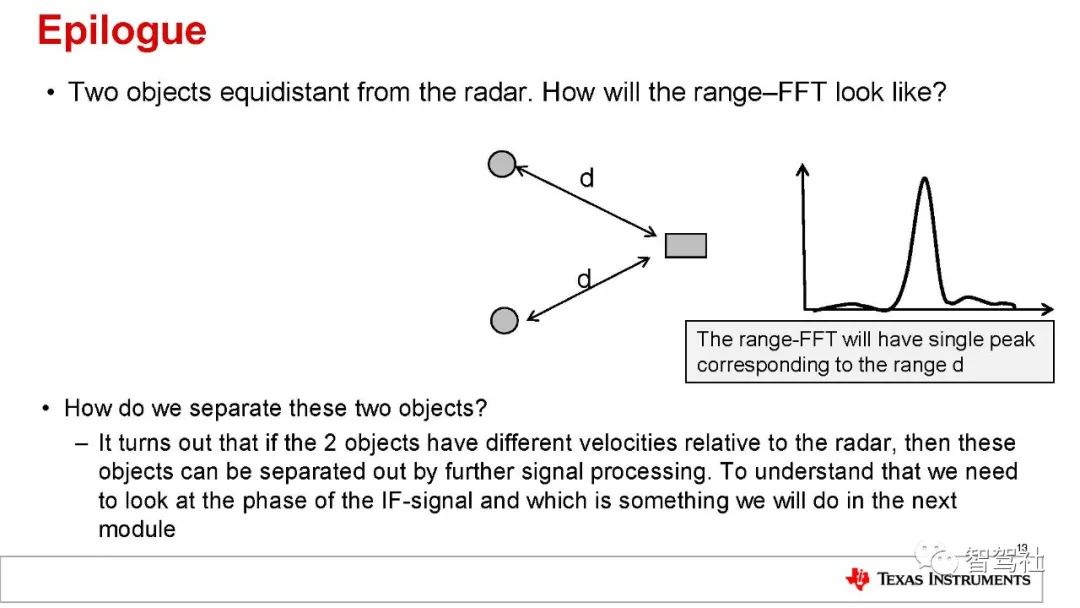
距离分辨率是辨别两个或更多物体的能力。当两个物体靠近到某个位置时，雷达系统将不再能够将二者区分开物体。傅里叶变换理论指出，通过延长 IF 信号，可以提高分辨率。

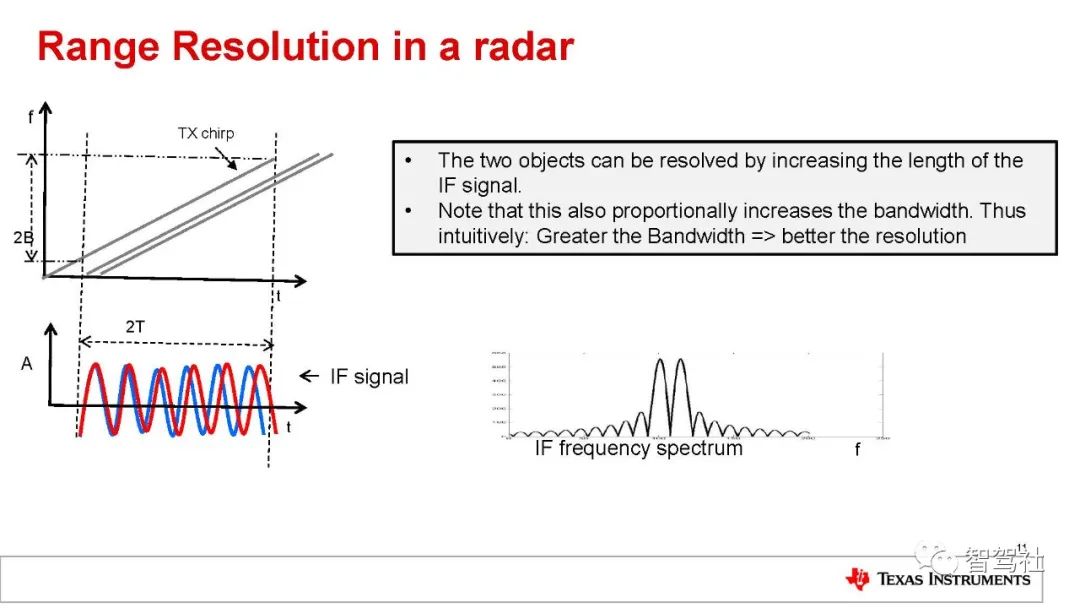
要延长 IF 信号，还必须按比例增加带宽。延长的IF 信号会产生一个有两个分离峰值的 IF 谱。

傅里叶变换理论还指出，观测窗口 (T) 可以分辨间隔超过 1/THz的频率分量。这意味着只要频率差满足方程式 8 中给出的关系，就可以分辨两个 IF 单音信号的

其中 Tc 是观测时间长度。

由于

，方程式 8 可以表达为：

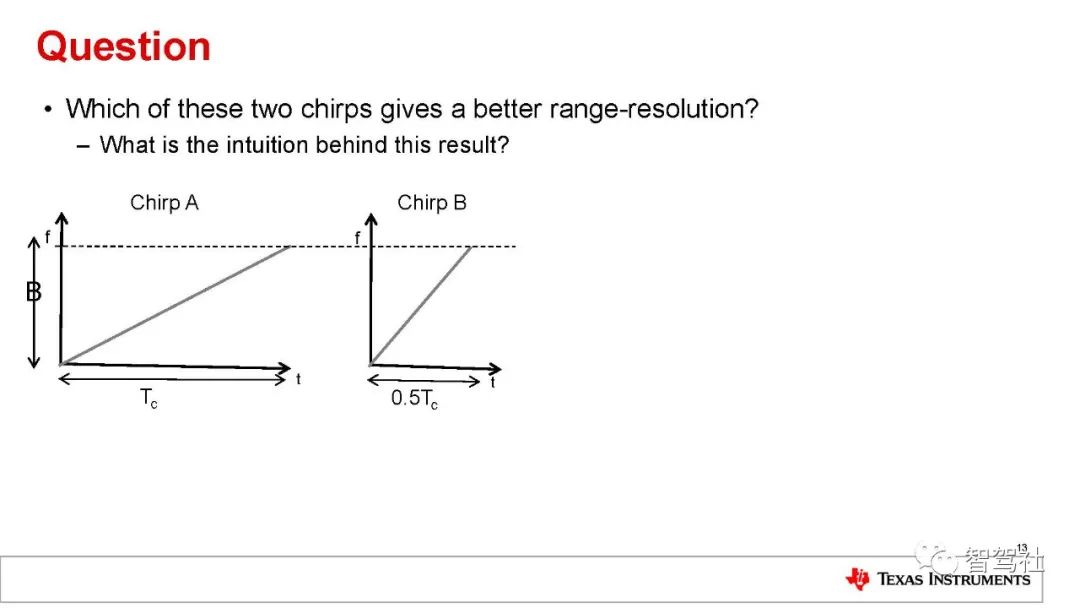
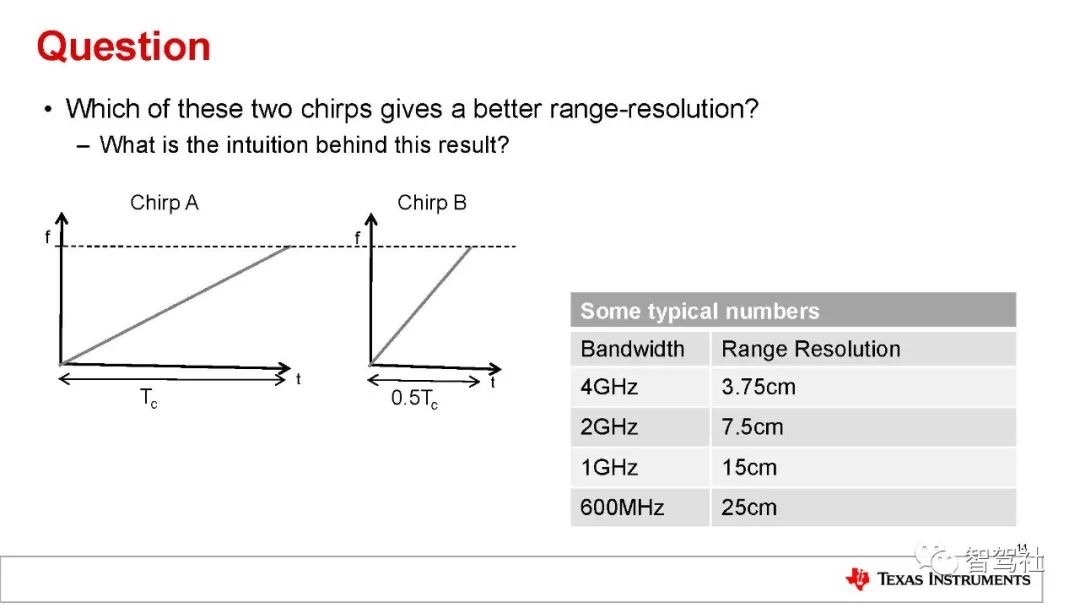
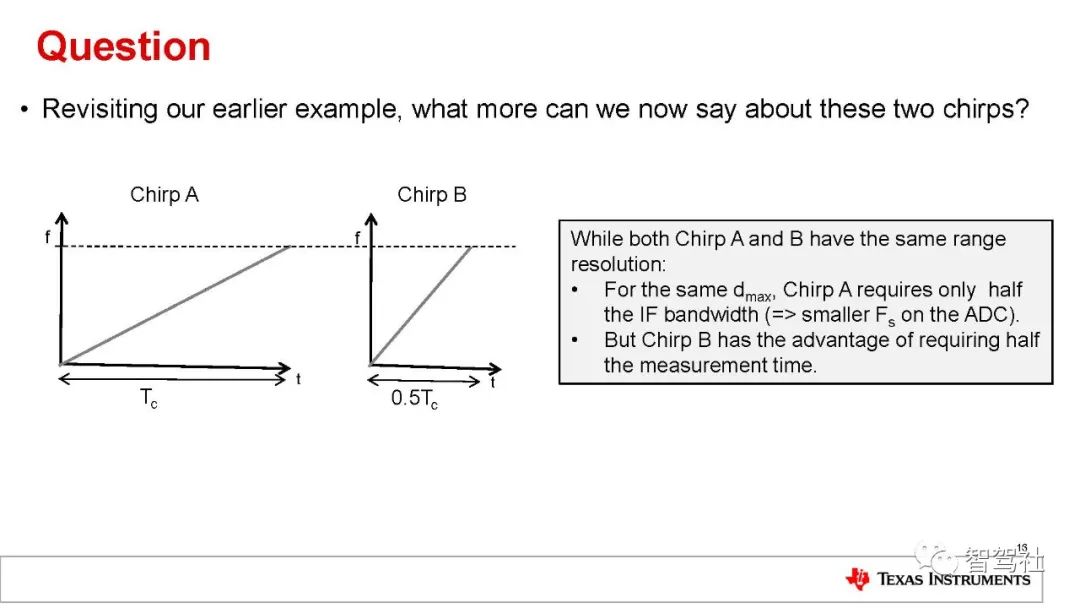
距离分辨率 (dRes) 仅取决于线性调频脉冲扫频的带宽（方程式 9）：

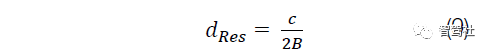
因此，线性调频脉冲带宽为数 GHz 的 FMCW 雷达将有约为数厘米的距离分辨率（例如，4GHz 的线性调频脉冲带宽可转化为 3.75cm的距离分辨率）。关于速度和角度的介绍，后续将继续更新，欢迎关注，收藏与转发。