🎬慕斯主页:修仙—别有洞天
♈️今日夜电波:宙でおやすみ
1:02━━━━━━️💟──────── 2:45
🔄 ◀️ ⏸ ▶️ ☰
💗关注👍点赞🙌收藏您的每一次鼓励都是对我莫大的支持😍
目录
62.不同路径
解题思路:
63.不同路径||
解题思路:
LCR 166.珠宝的最高价值
解题思路:
931.下降路径最小和
解题思路:
64.最小路径和
解题思路:
62.不同路径
62. 不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:

输入:m = 3, n = 7
输出:28示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下示例 3:
输入:m = 7, n = 3
输出:28示例 4:
输入:m = 3, n = 3
输出:6提示:
- 1 <= m, n <= 100
- 题目数据保证答案小于等于 2 * 109
解题思路:
1、状态表示:我们根据经验加题目要求,很明显的看出本题是一个二维数组的dp。对于二维dp我们可以按照以[i,j]为结尾时,巴拉巴拉 的模板来进行描述。本题的状态表示为:dp[i][j]表示:走到[i,j]位置时,一共有多少种方式。
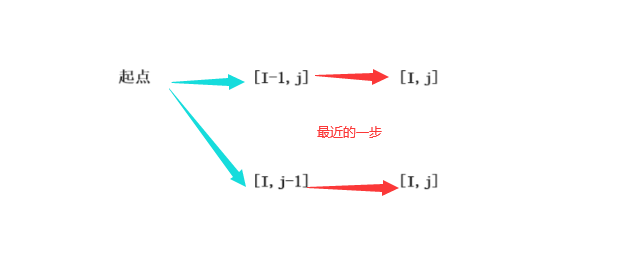
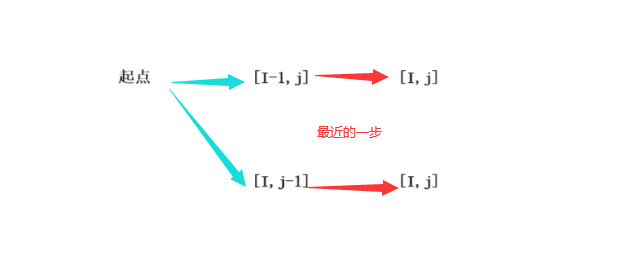
2、状态转移方程:根据题意,我们按照最近的一步划分问题。可知有两种最近的一步,即:
因此,我们可以根据上述的思想写出状态转移方程:
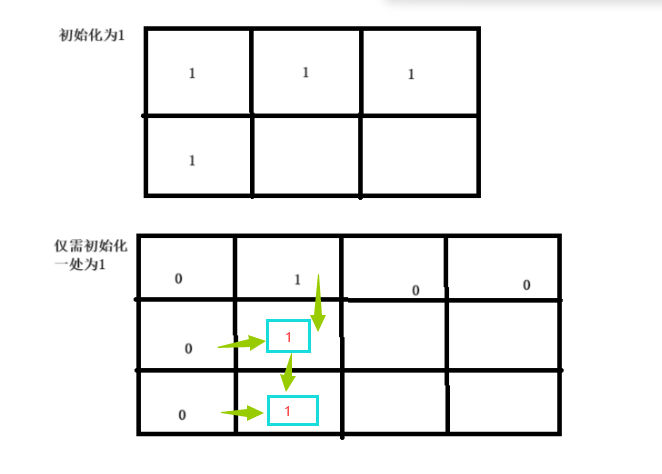
3、初始化(重点):在这里需要根据状态转移表示进行初始化,根据上面的状态转移方程,我们可以知道如果直接初始化需要将dp[0][j]、dp[i][0]都等于1才能完成初始化。但是我们在这里多加一横多加一列来初始化,让初始化更简单,也是防止越界。可以根据下图理解:
4、填表顺序:从上往下,从左往右填写。
5、返回值:dp[i][j]
因此我们写出如下题解:
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m+1,vector<int>(n+1));
dp[0][1]=1;
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
dp[i][j]=dp[i-1][j]+dp[i][j-1];
}
}
return dp[m][n];
}
};63.不同路径||
63. 不同路径 II
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右示例 2:

输入:obstacleGrid = [[0,1],[0,0]]
输出:1提示:
- m == obstacleGrid.length
- n == obstacleGrid[i].length
- 1 <= m, n <= 100
- obstacleGrid[i][j] 为 0 或 1
解题思路:
1、状态表示:我们根据经验加题目要求,很明显的看出本题是一个二维数组的dp。本题是上一题的拓展,只是多了一个障碍而已。本题的状态表示为:dp[i][j]表示:走到[i,j]位置时,一共有多少种方式。由于多了一个障碍,我们只需要加上一个判断:if(obstacleGrid[i-1][j-1]!=1)即可规避障碍。
2、状态转移方程:实际上还是和上一题一样的,即:dp[i][j]=dp[i-1][j]+dp[i][j-1];
3、初始化(重点):同上一题
4、填表顺序:从上往下,从左往右填写。
5、返回值:dp[i][j]
因此我们写出如下题解:(需要注意我们的dp表是加了一行一列的,因此对于obstacleGrid要对应上需要横和列都-1)
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
vector<vector<int>> dp(obstacleGrid.size()+1,vector<int>(obstacleGrid[0].size()+1));
dp[0][1]=1;
for(int i=1;i<=obstacleGrid.size();i++)
{
for(int j=1;j<=obstacleGrid[0].size();j++)
{
if(obstacleGrid[i-1][j-1]!=1)
{
dp[i][j]=dp[i-1][j]+dp[i][j-1];
}
}
}
return dp[obstacleGrid.size()][obstacleGrid[0].size()];
}
};LCR 166.珠宝的最高价值
LCR 166. 珠宝的最高价值
现有一个记作二维矩阵 frame 的珠宝架,其中 frame[i][j] 为该位置珠宝的价值。拿取珠宝的规则为:
- 只能从架子的左上角开始拿珠宝
- 每次可以移动到右侧或下侧的相邻位置
- 到达珠宝架子的右下角时,停止拿取
注意:珠宝的价值都是大于 0 的。除非这个架子上没有任何珠宝,比如 frame = [[0]]。
示例 1:
输入: frame = [[1,3,1],[1,5,1],[4,2,1]]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最高价值的珠宝提示:
- 0 < frame.length <= 200
- 0 < frame[0].length <= 200
解题思路:
1、状态表示:我们根据经验加题目要求,很明显的看出本题是一个二维数组的dp。因此写出状态表示:dp[i][j]表示:到达[i,j]位置时,此时的最大值。
2、状态转移方程:根据题意,我们可知只能向左或者向右移动即:
每次移动都会拿珠宝,因此写出状态转移方程:
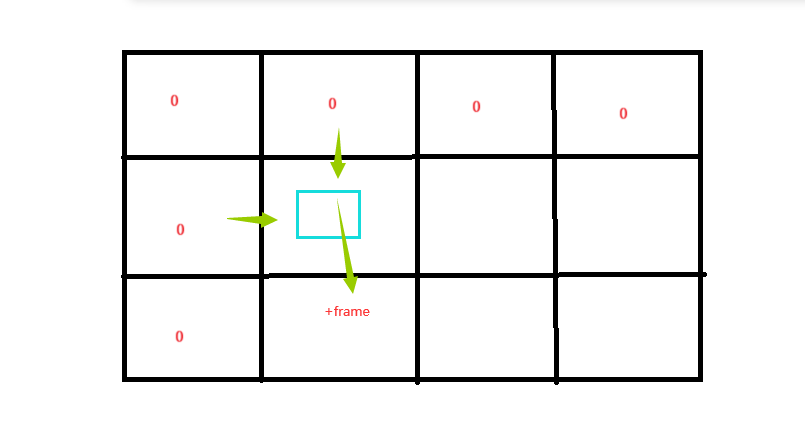
3、初始化(重点):我们多加上一横以及一列让初始化更简单,也是防止越界。根据题意,我们可以发现:要使dp表正确,我们仅需将dp[0][j]、dp[i][0]初始化为0即可,如下图示:
4、填表顺序:从上往下,从左往右填写。
5、返回值:dp[i][j]
因此我们写出如下题解:
class Solution {
public:
int jewelleryValue(vector<vector<int>>& frame) {
int n=frame.size();
int m=frame[0].size();
vector<vector<int>> dp(n+1,vector<int>(m+1));
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
dp[i][j]=max(dp[i-1][j],dp[i][j-1])+frame[i-1][j-1];
}
}
return dp[n][m];
}
};931.下降路径最小和
931. 下降路径最小和
给你一个 n x n 的 方形 整数数组 matrix ,请你找出并返回通过 matrix 的下降路径 的 最小和 。
下降路径 可以从第一行中的任何元素开始,并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列(即位于正下方或者沿对角线向左或者向右的第一个元素)。具体来说,位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。
示例 1:
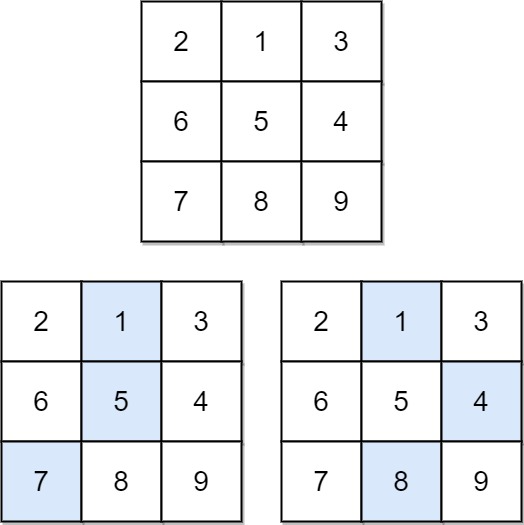
输入:matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出:13
解释:如图所示,为和最小的两条下降路径示例 2:
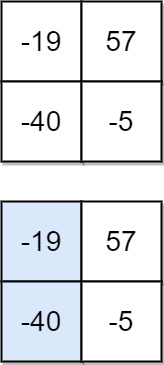
输入:matrix = [[-19,57],[-40,-5]]
输出:-59
解释:如图所示,为和最小的下降路径提示:
- n == matrix.length == matrix[i].length
- 1 <= n <= 100
- -100 <= matrix[i][j] <= 100
解题思路:
1、状态表示:我们根据经验加题目要求,很明显的看出本题是一个二维数组的dp。状态表示为:dp[i][j]表示: 到达[i,j]位置是,最小的下降路径。
2、状态转移方程:dp[i][j]=min(min(dp[i-1][j-1],dp[i-1][j]),dp[i-1][j+1])+matrix[i-1][j-1];如何d得出来的呢?我们可以从[i-1,j-1]->[i,j] [i-1,j]->[i,j] [i-1,j+1]->[i,j] 可以得出如下:
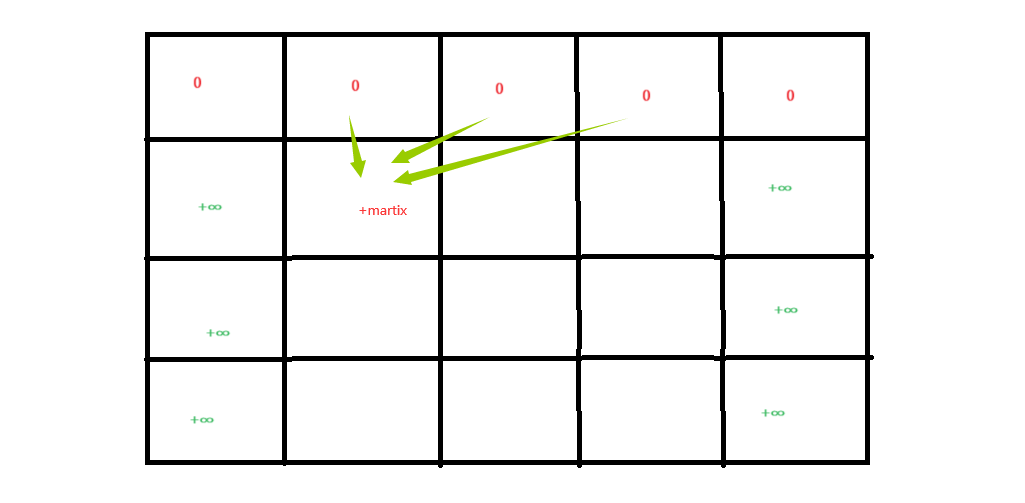
3、初始化(重点):根据题意,我们可以发现:要使dp表正确,我们需要多加一横以及两列,并且将最左的以及最右的两列初始化为最大,第一横初始化为0。(简化操作:现将全部初始化最大,第一横初始化为0)如下图所示:
4、填表顺序:从上往下
5、返回值:最后一横的最小值。
因此我们写出如下题解:
class Solution {
public:
int minFallingPathSum(vector<vector<int>>& matrix) {
int n=matrix.size(),m=matrix[0].size();
vector<vector<int>> dp(n+1,vector<int>(m+2,INT_MAX));
for(int i=0;i<m+2;i++)
{
dp[0][i]=0;
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
dp[i][j]=min(min(dp[i-1][j-1],dp[i-1][j]),dp[i-1][j+1])+matrix[i-1][j-1];
}
}
int min=INT_MAX;
for(int j=1;j<=m;j++)
{
if(min>dp[n][j])
min=dp[n][j];
}
return min;
}
};64.最小路径和
64. 最小路径和
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
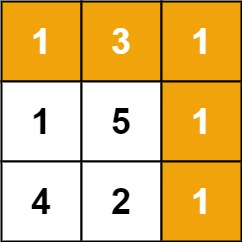
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12提示:
- m == grid.length
- n == grid[i].length
- 1 <= m, n <= 200
- 0 <= grid[i][j] <= 200
解题思路:
1、状态表示:我们根据经验加题目要求,很明显的看出本题是一个二维数组的dp。dp[i][j] 表示:达到[i,j]位置,最小路径和。
2、状态转移方程: dp[i][j]=min(dp[i][j-1],dp[i-1][j])+grid[i-1][j-1];
3、初始化(重点):多加一横以及一列,我们需要保证里面的值要保证后面的值是正确的。因此我们将所有值都先初始化为最大值,再将dp[0][1]或者dp[1][0]初始化为0即可。后续也需要注意下标的映射关系。
4、填表顺序:从上往下,从左往右填写。
5、返回值:dp[i][j]
因此我们写出如下题解:
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int n=grid.size();
int m=grid[0].size();
vector<vector<int>> dp(n+1,vector<int>(m+1,INT_MAX));
dp[0][1]=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
dp[i][j]=min(dp[i][j-1],dp[i-1][j])+grid[i-1][j-1];
}
}
return dp[n][m];
}
};
感谢你耐心的看到这里ღ( ´・ᴗ・` )比心,如有哪里有错误请踢一脚作者o(╥﹏╥)o!

给个三连再走嘛~

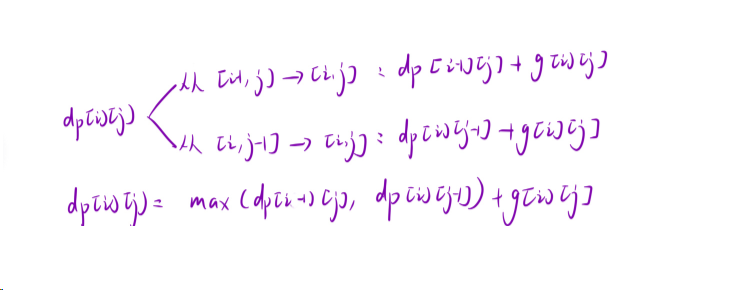

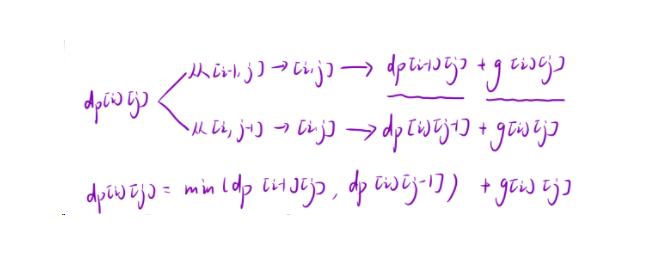



![[linux][xdp] xdp 入门](https://img-blog.csdnimg.cn/direct/defd49fdfb1e473fa7d37798ec1bd8a1.png)







![Twing模板注入 [BJDCTF2020]Cookie is so stable1](https://img-blog.csdnimg.cn/direct/d77953361c494c6382cc37f6af849705.png)