PageRank算法,即网页排名算法,由Google创始人Larry Page在斯坦福上学的时候提出来的。该算法用于对网页进行排名,排名高的网页表示该网页被访问的概率高。PageRank算法计算每一个网页的PageRank值,然后根据这个值的大小对网页的重要性进行排序。它的思想是模拟一个悠闲的上网者,上网者首先随机选择一个网页打开,然后在这个网页上呆了几分钟后,跳转到该网页所指向的链接,这样漫无目的地在网页上跳来跳去,PageRank就是估计这个悠闲的上网者分布在各个网页上的概率。
该算法的主要思想有两点,针对一般的有向网络:
1.如果多个网页指向某个网页A,则网页A的排名较高。
2.如果排名高A的网页指向某个网页B,则网页B的排名也较高,即网页B的排名受指向其的网页的排名的影响。
▍PageRank算法案例
案例一:
假设一个由4个网页组成的群体:A,B,C和D。如果所有页面都只链接至A,那么A的PR值将是B,C及D的Pagerank总和。
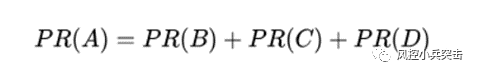
重新假设B链接到A和C,C只链接到A,并且D链接到全部其他的3个页面。一个页面总共只有一票。所以B给A和C每个页面半票。以同样的逻辑,D投出的票只有三分之一算到了A的PageRank上。
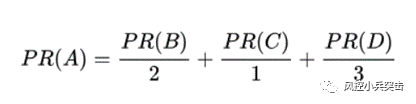
d为阻尼系数,其意义是,在任意时刻,用户到达某页面后并继续向后浏览的概率,该数值是根据上网者使用浏览器书签的平均频率估算而得,通常d=0.85。
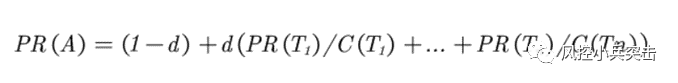
PR(A)是页面A的PR值
PR(Ti)是页面Ti的PR值,在这里,页面Ti是指向A的所有页面中的某个页面
C(Ti)是页面Ti的出度,也就是Ti指向其他页面的边的个数
一般会初始化每一个页面的PR值,然后迭代循环n次,直到PR值稳定,一般要设置收敛条件:比如上次迭代结果与本次迭代结果小于某个误差,我们结束程序运行;比如还可以设置最大循环次数。
案例二:
假设A网页有到B网页的连接,B网页有到C网页的连接,C网页有到A网页的连接,表示成A --> B–> C–> A的有向边,如图:

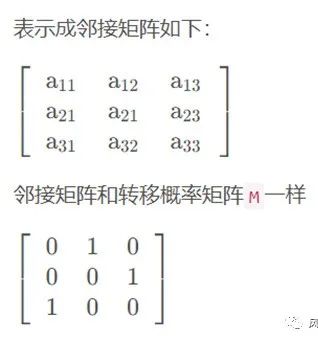
假设A网页还有到C网页的出链,那么有1/2的概率会到C网页,1/2的概率到B网页,则邻接矩阵【按列进行归一化后】M变成了转移概率矩阵:
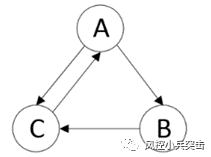

M的第一行代表A网页出链到A , B,C网页的概率,第二行代表B网页出链到A , B,C网页的概率,第三行代表C网页出链到A , B,C网页的概率,我们从邻接矩阵可以发现,转移概率矩阵的行的概率和为1【按列归一化的结果】,只要保证这点,则后期PageRank迭代的时候Un就可以收敛。
假如某个节点不存在外链,也就是说邻接矩阵的某一列出链到其他的概率都为0,这样就造成邻接矩阵的某一列都为0,这样就会造成迭代的时候,U的元素都会变成0。引入了阻尼系数α,迭代算法进行改进。
在实际应用中,为了有效避免上述两个问题,会使用到一个小技巧,就是假设每个节点都有一个假想的外链指向其它任一节点,这样整个图就变成了一个强连通图了。为了尽量不影响最终计算的PageRank值,节点通过假想外链传递的PageRank值会乘一个权重因子β【β=1−α】,β一般取0.2或者更小。
▍PageRank算法应用场景
网页之间会形成一个网络,是我们的互联网,论文之间也存在着相互引用的关系,可以说我们所处的环境就是各种网络的集合。只要是有网络的地方,就存在出链和入链,就会有PR权重的计算,也就可以运用我们今天讲的PageRank算法。
我们可以把PageRank算法延展到社交网络领域中。例如在微博上,如果我们想要计算某个人的影响力,该怎么做呢?一个人的微博粉丝数并不一定等于他的实际影响力。如果按照PageRank算法,还需要看这些粉丝的质量如何。如果有很多明星或者大V关注,那么这个人的影响力一定很高。如果粉丝是通过购买僵尸粉得来的,那么即使粉丝数再多,影响力也不高。PageRank算法适用于网页排序、社交网络重点人物发掘,可用于找出网络中影响力较高的用户或者名气较大的网站。
在信贷风控场景中,构建进件客户之间的关联网络,这个网络内的该节点周围存在黑名单客户较多,某个节点的PR值越高,说明这个节点在网络中的中心度越高,该节点为黑名单客户的概率越大。
在贷后资金归集的场景中,构建交易流水的关联网络,这个网络内的节点PR值越大,越有可能是资金归集账户。节点中心度在交易网络中,可以衡量网络中资金流向某个节点的概率,流入节点概率越大则节点的中心度越高。因此,我们可以通过PageRank算法计算节点PR值。针对初步筛选出的风险团伙,计算成果中各个节点的PR值,每个团伙中PR值最高的用户将被认为是归集账户,归集账户所对应的团伙会被最终认定为是聚集性风险团伙、贷后资金归集的团伙。
▍PageRank算法简单实践
import networkx as nx
# 创建有向图
G = nx.DiGraph()
# 有向图之间边的关系
edges = [("A", "B"), ("A", "C"), ("A", "D"), ("B", "A"), ("B", "D"), ("C", "A"), ("D", "B"), ("D", "C")]
for edge in edges:
G.add_edge(edge[0], edge[1])
pagerank_list = nx.pagerank(G, alpha=1)
print("pagerank 值是:", pagerank_list)pagerank 值是:{'A': 0.33333396911621094, 'B': 0.22222201029459634, 'C': 0.22222201029459634, 'D': 0.22222201029459634}