【统计分析数学模型】判别分析(四):机器学习分类算法
- 一、机器学习分类算法
- 1. 交叉验证方法
- 2. 案例数据集
- 3. 数据标准化
- 二、决策树模型
- 1. 基本原理
- 2. 计算步骤
- 3. R语言实现
- 三、K最邻近分类
- 1. 基本原理
- 2. K值的选择
- 3. R语言实现
- 四、支持向量机
- 1.基本原理
- 2. R语言实现
- 五、神经网络分类
- 1. 基本原理
- 2. BP神经网络
- 3. R语言实现
- 六、随机森林分类
- 1. 基本原理
- 2. R语言实现
- 七、总结
一、机器学习分类算法
机器学习中的分类算法也常常用来解决判别分析问题。常见的分类算法包括决策树、K最邻近、支持向量机、神经网络、随机森林等。
1. 交叉验证方法
在用这些算法建立分类模型时,如果用全部数据建立模型并用回代法进行模型的内部验证,可能会出现过度拟合现象。因此,在建模时需要进行交叉验证以避免过度拟合问题。常用的交叉验证方法有以下3种:
- 保留交叉验证(hand-out cross validation)
将样本集随机分成训练集(training set)和验证集(test set),比例通常是7∶3或8∶2。使用模型在训练集上学习得到假设,然后使用验证集对假设进行验证,看模型预测的准确性,选择误差小的模型。 - k折交叉验证(k-fold cross validation)
把样本集分成k份,分别使用其中的k−1份作为训练集,剩下的1份作为交叉验证集,最后通过所有模型的平均误差来评估模型参数。 - 留一法验证(leave-one-out validation)
实质上是n折交叉验证,n是样本集的大小,就是只留下一个样本来验证模型的准确性。
2. 案例数据集
以MASS包中的数据集Pima.tr和Pima.te为例说明常见机器学习分类算法的实现方法。
它们是居住在美国某地区皮马印第安人后裔中部分女性的糖尿病调查数据。两个数据框中的变量都是一样的,其含义如下。
- npreg:怀孕次数
- glu:血糖浓度
- bp:舒张压(单位:mmHg)
- skin:三头肌皮褶厚度(单位:mm)
- bmi:体质指数
- ped:糖尿病家族史因素
- age:年龄
- type:是否患有糖尿病(Yes/No)
其中,结局变量为type,其余均为数值型的预测变量。
3. 数据标准化
首先,加载这两个数据集并分别将它们作为训练集和测试集:
library(MASS)
data(Pima.tr)
data(Pima.te)
由于预测变量的测量单位之间有较大差异,下面用函数scale()将它们标准化,都转换为均值为0、标准差为1的变量,并将训练集命名为data.train,测试集命名为data.test:
data.train<-Pima.tr
data.train[,-8]<-scale(data.train[,-8])
data.test<-Pima.te
data.test[,-8]<-scale(data.test[,-8])
二、决策树模型
1. 基本原理
决策树(decision tree)模型 是一种简单易用的非参数分类方法。它不需要对数据的分布有任何的先验假设,计算速度快,结果也容易解释。
分类回归树方法(CART) 是决策树模型中的一种经典算法,CART分为分类树(classification tree)和回归树(regression tree)两种。
分类树用于因变量为分类数据的情况,树的末端为因变量的类别;回归树用于因变量为连续型变量的情况,树的末端给出相应类别中的因变量描述或预测。
2. 计算步骤
- 首先对所有自变量和所有分隔点进行评估,最佳的选择是使分隔后组内的数据“纯度”更高,即组内目标变量的变异最小;
- 再对分类树模型进行修剪或称为剪枝:如果不加任何限制,过度复杂的分类树模型很容易产生“过度拟合”的问题。
通常使用CP参数(complexity parameter)控制树的复杂度。CP参数取值越小,模型越复杂,越偏向于过度拟合。
通常的做法是先建立一个枝节较多的分类树模型,再使用交叉验证的方法来估计不同“剪枝”条件下各个模型的误差,从而选择误差最小的分类树模型。
3. R语言实现
library(rpart)
set.seed(123)
pima.rpart<-rpart(type~.,data=data.train,control=rpart.control(cp=0))
pima.rpart
决策树模型的输出结果看起来像是以树状形式排列的一系列if-else语句。每行括号前面的数字代表节点,行缩进表示分支,*表示叶节点,loss表示误差数量。各节点后括号里的数值代表了各类别的比例:
> pima.rpart
n= 200
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 200 68 No (0.66000000 0.34000000)
2) glu< -0.01484184 109 15 No (0.86238532 0.13761468)
4) age< -0.3289163 74 4 No (0.94594595 0.05405405) *
5) age>=-0.3289163 35 11 No (0.68571429 0.31428571)
10) glu< -1.072718 9 0 No (1.00000000 0.00000000) *
11) glu>=-1.072718 26 11 No (0.57692308 0.42307692)
22) bp>=-0.2839819 19 6 No (0.68421053 0.31578947) *
23) bp< -0.2839819 7 2 Yes (0.28571429 0.71428571) *
3) glu>=-0.01484184 91 38 Yes (0.41758242 0.58241758)
6) ped< -0.4923593 35 12 No (0.65714286 0.34285714)
12) glu< 1.32724 27 6 No (0.77777778 0.22222222) *
13) glu>=1.32724 8 2 Yes (0.25000000 0.75000000) *
7) ped>=-0.4923593 56 15 Yes (0.26785714 0.73214286)
14) bmi< -0.597043 11 3 No (0.72727273 0.27272727) *
15) bmi>=-0.597043 45 7 Yes (0.15555556 0.84444444) *
用plot()函数绘制分类树:
plot(pima.rpart,uniform=TRUE,margin=0.1)
text(pima.rpart,use.n=TRUE)
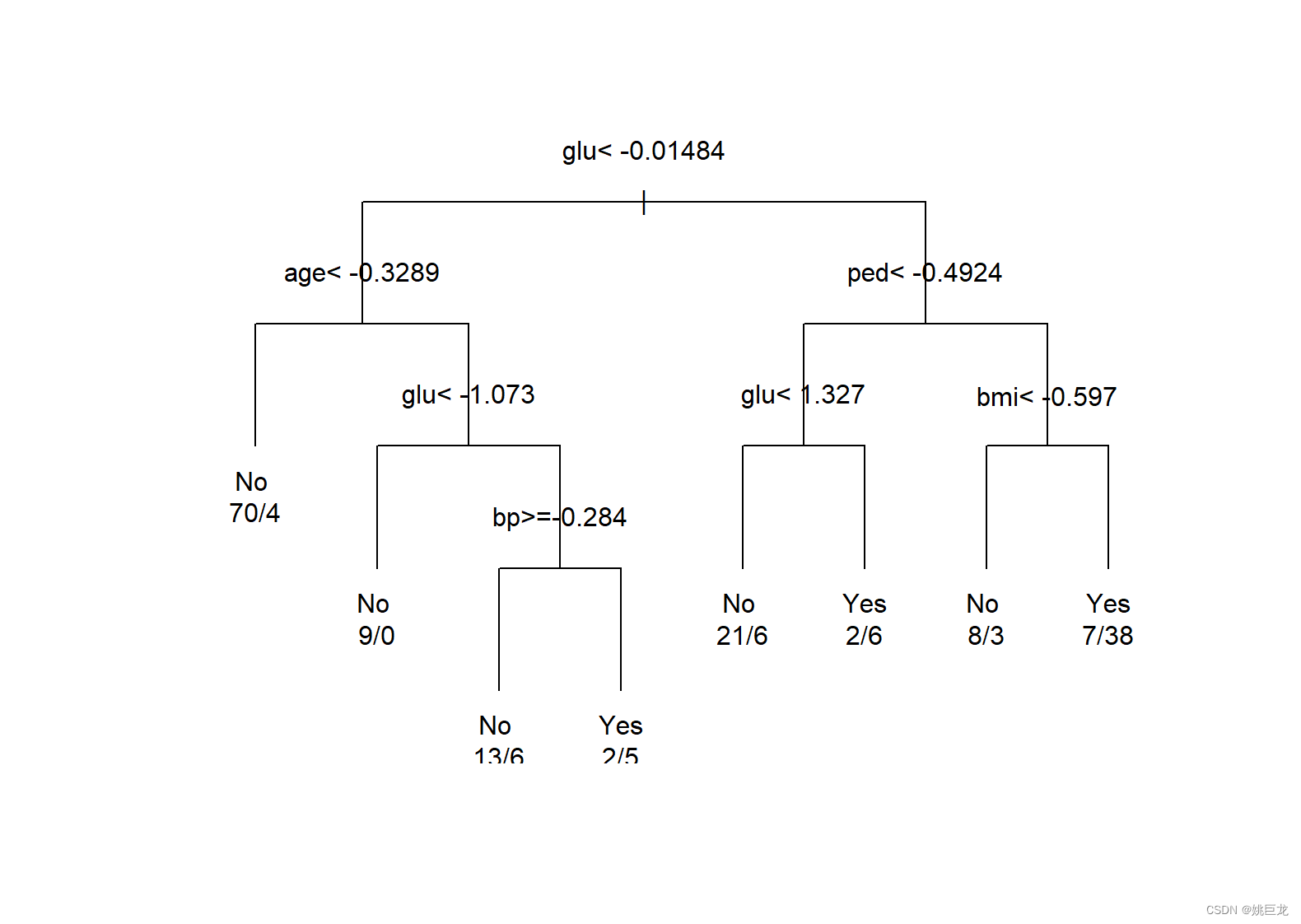
寻找最小xerror值对应的CP值,并由此CP值决定树的规模,再用函数prune()对树模型进行剪枝:
cptable<-as.data.frame(pima.rpart$cptable)
cpvalue<-cptable[which.min(cptable$xerror),"CP"]
cpvalue#最小的CP值
prune.model<-prune(pima.rpart,cpvalue)
画出剪枝后的模型对象prune.model的分类树模型:
plot(prune.model,uniform=TRUE,margin=0.1)
text(prune.model,use.n=TRUE)
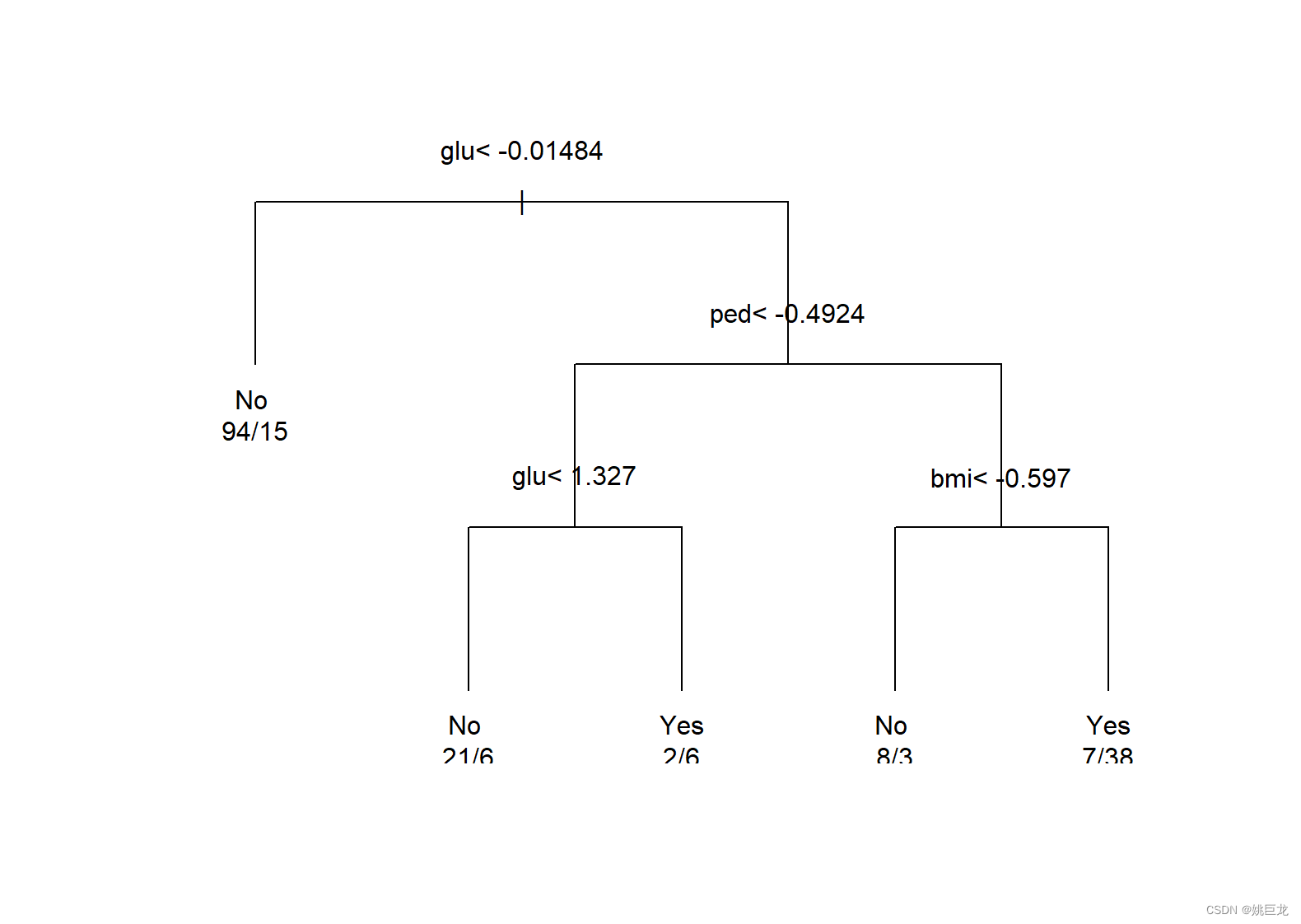
分类树模型对于建模数据的预测结果:
probs.rp<-predict(prune.model)
head(probs.rp)
pred.train<-predict(prune.model,type="class")
pred.train[1:6]#查看前6个分类结果
结果如下:
> head(probs.rp)
No Yes
[1,] 0.8623853 0.1376147
[2,] 0.2500000 0.7500000
[3,] 0.8623853 0.1376147
[4,] 0.7777778 0.2222222
[5,] 0.8623853 0.1376147
[6,] 0.8623853 0.1376147
> pred.train[1:6]
[1] No Yes No No No No
Levels: No Yes
建立混淆矩阵查看判别效果:
cm.train<-table(pred.train,data.train$type)
cm.train
sum(diag(cm.train))/sum(cm.train)#计算回判正确率
结果如下:
> cm.train
pred.train No Yes
No 123 24
Yes 9 44
> sum(diag(cm.train))/sum(cm.train)#计算回判正确率
[1] 0.835
一共有33名对象被错判,回判正确率为83.5%,这个预测是针对训练集进行的。
下面用测试数据进行外部验证:
pred.test<-predict(prune.model,newdata=data.test[,-8],type="class")
cm.test<-table(pred.test,data.test$type)
cm.test
sum(diag(cm.test))/sum(cm.test)#计算预测正确率
结果如下:
> cm.test
pred.test No Yes
No 193 49
Yes 30 60
> sum(diag(cm.test))/sum(cm.test)#计算预测正确率
[1] 0.7620482
预测正确率为76.2%。一般来说,外部验证的正确率会低于内部验证的正确率(回判正确率)。
三、K最邻近分类
1. 基本原理
K最邻近(K-nearest neighbor, KNN)算法是一个理论上比较成熟的算法,也是最简单的分类算法之一。
其基本思路是,如果一个样品在特征空间中与K个最邻近(或最相似)样品中的大多数属于某一个类别,则将该样品判为这个类别。
2. K值的选择
KNN算法在进行判别时,主要依靠样品周围若干邻近样品的信息,选择不同的K值可能得到不同的分类结果。
如果选择较小的K值,就相当于用较小邻域中的训练样品进行预测,“学习”的近似误差会减小,只有与待判样品较近的训练样品才会对预测结果起作用。但其缺点是“学习”的估计误差会增大,预测结果对邻近的样品点非常敏感。换句话说,K值的减小意味着整体模型变得复杂,容易发生过度拟合现象。
如果选择较大的K值,就相当于用较大邻域中的训练样品进行预测。其优点是可以减少“学习”的估计误差,但缺点是“学习”的近似误差会增大。这时与待判样品较远的(不相似的)训练样品也会对预测起作用,使预测发生错误。K值增大就意味着整体模型变得简单。
K值的选择反映了对近似误差与估计误差的权衡,通常可以尝试选择不同的K比较模型的预测效果,从而选择预测效果最优的K。
3. R语言实现
class包里的函数knn()可以实现基本的KNN算法,在函数中需要输入训练集(train)、测试集(test)、训练集里样品的类别标签(cl)和邻近点的个数(K)等。
library(caret)
set.seed(123)#设定随机数种子
ctrl<-trainControl(method="repeatedcv",number=10,repeats=3)
tunedf<-data.frame(k=3:10)
knnmodel<-train(type~.,data=data.train,method="knn",trControl=ctrl,tuneGrid=tunedf)
plot(knnmodel)
对每次抽样得到的数据都进行10重交叉验证,即得到30次验证的结果。
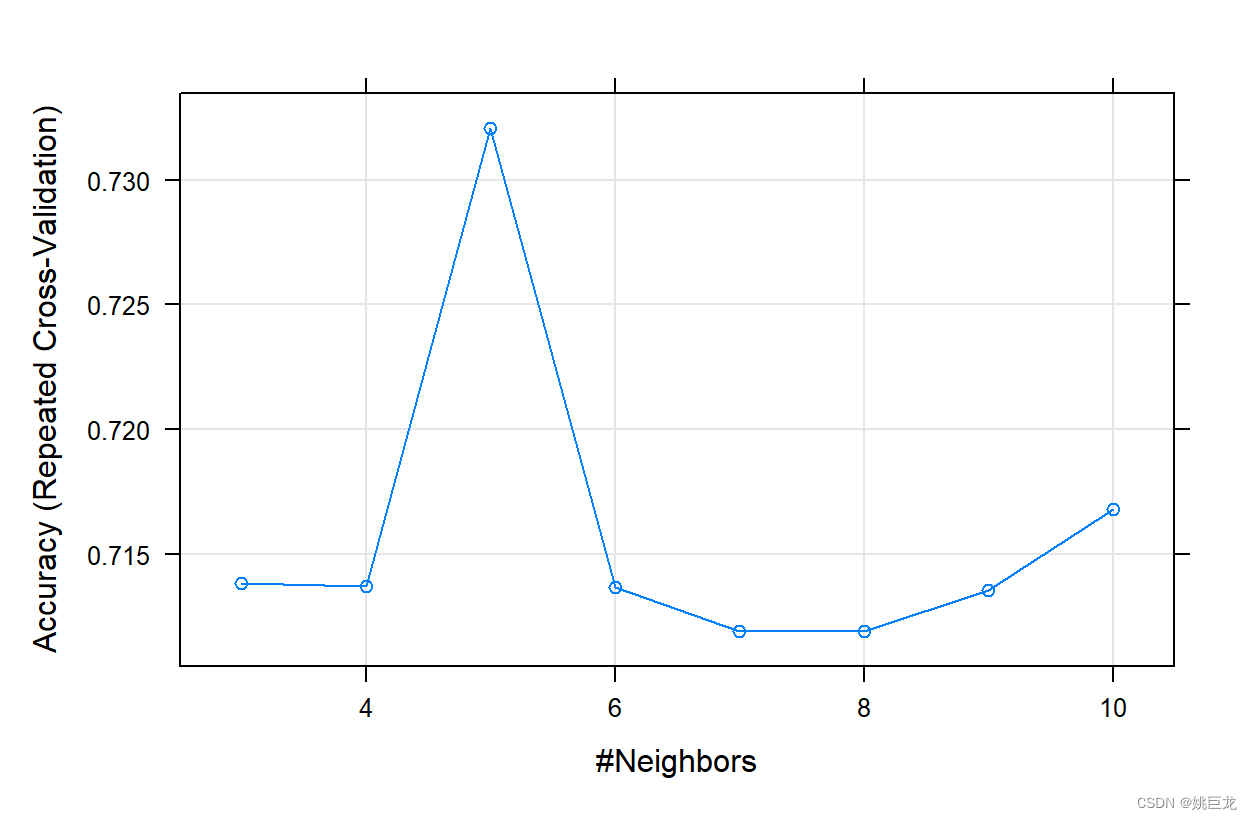
从图中可以看出,对于该数据集,当K取5时模型的预测效果最佳。
计算回判正确率和预测正确率:
knn.pred.train<-predict.train(knnmodel)
confusionMatrix(knn.pred.train,data.train$type)
knn.pred.test<-predict(knnmodel,newdata=data.test[,-8])
confusionMatrix(knn.pred.test,data.test$type)
结果如下:
> confusionMatrix(knn.pred.train,data.train$type)
Confusion Matrix and Statistics
Reference
Prediction No Yes
No 124 26
Yes 8 42
Accuracy : 0.83
95% CI : (0.7706, 0.8793)
No Information Rate : 0.66
P-Value [Acc > NIR] : 6.299e-08
Kappa : 0.5952
Mcnemar's Test P-Value : 0.003551
Sensitivity : 0.9394
Specificity : 0.6176
Pos Pred Value : 0.8267
Neg Pred Value : 0.8400
Prevalence : 0.6600
Detection Rate : 0.6200
Detection Prevalence : 0.7500
Balanced Accuracy : 0.7785
'Positive' Class : No
> confusionMatrix(knn.pred.test,data.test$type)
Confusion Matrix and Statistics
Reference
Prediction No Yes
No 196 54
Yes 27 55
Accuracy : 0.756
95% CI : (0.7062, 0.8013)
No Information Rate : 0.6717
P-Value [Acc > NIR] : 0.0005027
Kappa : 0.4094
Mcnemar's Test P-Value : 0.0038661
Sensitivity : 0.8789
Specificity : 0.5046
Pos Pred Value : 0.7840
Neg Pred Value : 0.6707
Prevalence : 0.6717
Detection Rate : 0.5904
Detection Prevalence : 0.7530
Balanced Accuracy : 0.6918
'Positive' Class : No
回判正确率为83.0%,预测正确率为75.6%。
这表明对于当前的数据集,KNN算法的分类效果比rpart算法稍差。
四、支持向量机
1.基本原理
支持向量机(support vector machine, SVM)是一种有监督学习的分类和回归分析方法。它的基本思想是对于给定的训练数据,在数据的特征空间中找到一个超平面(即分隔超平面),将数据划分为两个类别,并且使这个超平面与数据最近的样本点(支持向量)距离最大,从而得到一个最优的决策边界。SVM在解决高维数据分类问题上具有很高的效率,并且能够解决非线性分类问题。
笔者在2019年记录过SVM相关理论的学习,可以帮助更加详细理解理解SVM的4个关键概念:分隔超平面、最大边缘超平面、软边缘、核函数。
SVM学习笔记(一)——介绍与原理推导
SVM学习笔记(二)——软间隔(soft-margin)
SVM学习笔记(三)——核函数
SVM学习笔记(四)——SVM模型实例
SVM学习笔记(五)——在Python下使用不同核函数进行训练
2. R语言实现
现在仍以前面的例子,使用多重交叉验证的方法来建立模型:
set.seed(123)
ctrl<-trainControl(method="repeatedcv",number=10,repeats=3)
tunedf<-data.frame(C=seq(0.1,1,length=10))
svmmodel<-train(type~.,data=data.train,
method="svmRadialCost",
trControl=ctrl,
tuneGrid=tunedf)
plot(svmmodel)
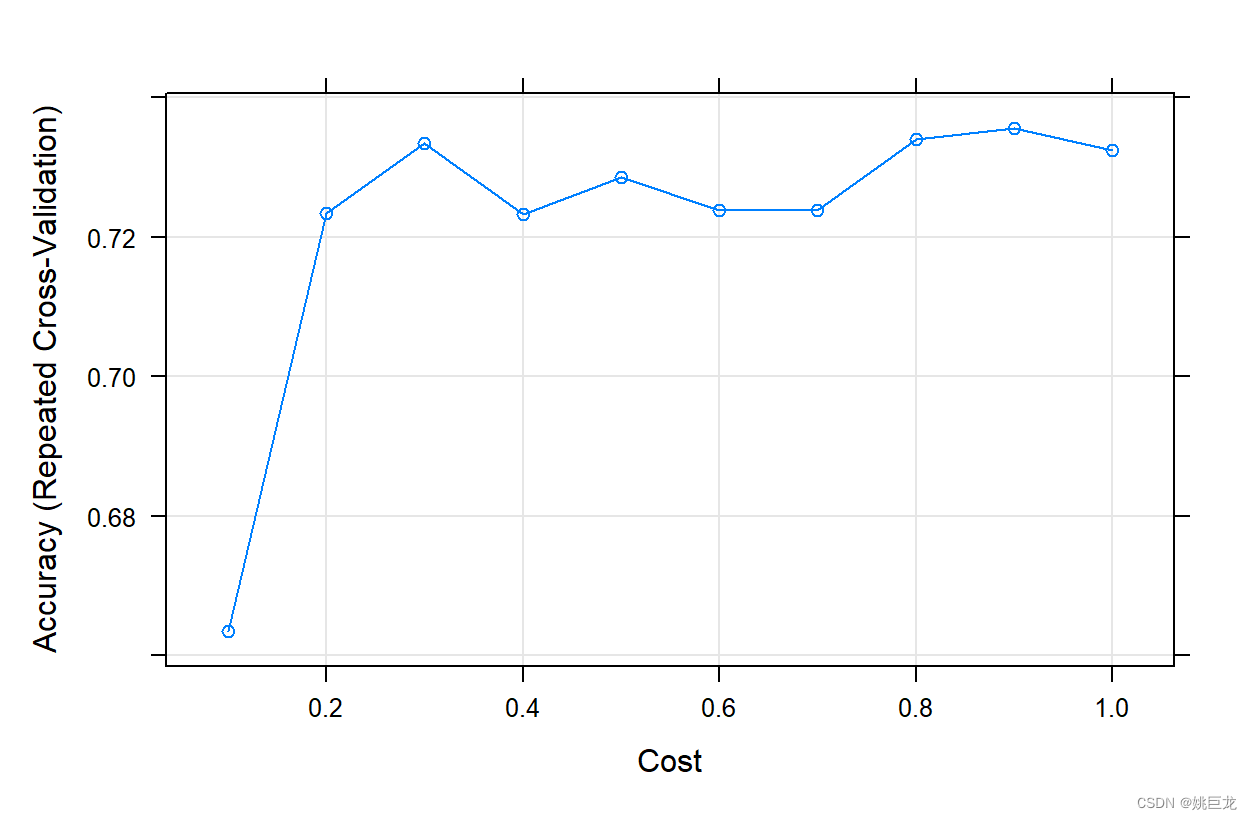
计算回判正确率和预测正确率:
svm.pred.train<-predict.train(svmmodel)
confusionMatrix(svm.pred.train,data.train$type)
svm.pred.test<-predict(svmmodel,newdata=data.test[,-8])
confusionMatrix(svm.pred.test,data.test$type)
结果如下:
> confusionMatrix(svm.pred.train,data.train$type)
Confusion Matrix and Statistics
Reference
Prediction No Yes
No 121 26
Yes 11 42
Accuracy : 0.815
95% CI : (0.7541, 0.8663)
No Information Rate : 0.66
P-Value [Acc > NIR] : 8.89e-07
Kappa : 0.5645
Mcnemar's Test P-Value : 0.02136
Sensitivity : 0.9167
Specificity : 0.6176
Pos Pred Value : 0.8231
Neg Pred Value : 0.7925
Prevalence : 0.6600
Detection Rate : 0.6050
Detection Prevalence : 0.7350
Balanced Accuracy : 0.7672
'Positive' Class : No
> confusionMatrix(svm.pred.test,data.test$type)
Confusion Matrix and Statistics
Reference
Prediction No Yes
No 200 47
Yes 23 62
Accuracy : 0.7892
95% CI : (0.7413, 0.8318)
No Information Rate : 0.6717
P-Value [Acc > NIR] : 1.53e-06
Kappa : 0.4934
Mcnemar's Test P-Value : 0.005977
Sensitivity : 0.8969
Specificity : 0.5688
Pos Pred Value : 0.8097
Neg Pred Value : 0.7294
Prevalence : 0.6717
Detection Rate : 0.6024
Detection Prevalence : 0.7440
Balanced Accuracy : 0.7328
'Positive' Class : No
结果表明,回判正确率为81.5%,预测正确率约为78.9%。
五、神经网络分类
1. 基本原理
神经网络是一种运算模型,它由大量的节点(或称神经元)和它们之间的相互连接构成,每个节点代表一种特定的输出函数,称为激励函数(activation function)。
每两个节点间的连接都代表一个对于通过该连接信号的加权值,称为权重。网络的输出则依网络的连接方式、权重值和激励函数的不同而不同。
2. BP神经网络
BP神经网络是一种按照误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一。
P神经网络模型的结构包括输入层(input layer)、隐层(hide layer)和输出层(output layer)。nnet包中的函数nnet()可以实现BP神经网络算法,其中的重要参数如下。
| 参数 | 含义 |
|---|---|
| size | 隐层神经元的个数,数字越大模型越复杂。 |
| decay | 学习速率,是为了避免过度拟合,这个值一般在0~0.1,默认为0。 |
| linout | 隐层到输出层的函数形式,若是回归问题则设为TRUE,表示线性输出,若是分类问题则设为FALSE,表示非线性输出。 |
3. R语言实现
set.seed(123)
ctrl<-trainControl(method="repeatedcv",number=10,repeats=3)
tunedf<-expand.grid(decay=0.1,size=3:10)
nnetmodel<-train(type~.,data=data.train,
method="nnet",
trControl=ctrl,
tuneGrid=tunedf,
trace=FALSE)
nnetmodel
plot(nnetmodel)
结果显示,BP神经网络模型的参数在隐层神经元为9个时,准确率最高:
> nnetmodel
Neural Network
200 samples
7 predictor
2 classes: 'No', 'Yes'
No pre-processing
Resampling: Cross-Validated (10 fold, repeated 3 times)
Summary of sample sizes: 179, 180, 180, 181, 180, 180, ...
Resampling results across tuning parameters:
size Accuracy Kappa
3 0.7091353 0.3369336
4 0.7057477 0.3245978
5 0.7154845 0.3372826
6 0.7073893 0.3293559
7 0.7184670 0.3464772
8 0.6969591 0.3122613
9 0.7187469 0.3546736
10 0.7075647 0.3238119
Tuning parameter 'decay' was held constant at a value of 0.1
Accuracy was used to select the optimal model using the largest value.
The final values used for the model were size = 9 and decay = 0.1.

计算回判正确率和预测正确率:
nnet.pred.train<-predict(nnetmodel)
confusionMatrix(nnet.pred.train,data.train$type)
nnet.pred.test<-predict(nnetmodel,newdata=data.test[,-8])
confusionMatrix(nnet.pred.test,data.test$type)
结果如下:
> confusionMatrix(nnet.pred.train,data.train$type)
Confusion Matrix and Statistics
Reference
Prediction No Yes
No 126 12
Yes 6 56
Accuracy : 0.91
95% CI : (0.8615, 0.9458)
No Information Rate : 0.66
P-Value [Acc > NIR] : <2e-16
Kappa : 0.7951
Mcnemar's Test P-Value : 0.2386
Sensitivity : 0.9545
Specificity : 0.8235
Pos Pred Value : 0.9130
Neg Pred Value : 0.9032
Prevalence : 0.6600
Detection Rate : 0.6300
Detection Prevalence : 0.6900
Balanced Accuracy : 0.8890
'Positive' Class : No
> confusionMatrix(nnet.pred.test,data.test$type)
Confusion Matrix and Statistics
Reference
Prediction No Yes
No 190 41
Yes 33 68
Accuracy : 0.7771
95% CI : (0.7285, 0.8207)
No Information Rate : 0.6717
P-Value [Acc > NIR] : 1.585e-05
Kappa : 0.485
Mcnemar's Test P-Value : 0.4158
Sensitivity : 0.8520
Specificity : 0.6239
Pos Pred Value : 0.8225
Neg Pred Value : 0.6733
Prevalence : 0.6717
Detection Rate : 0.5723
Detection Prevalence : 0.6958
Balanced Accuracy : 0.7379
'Positive' Class : No
回判正确率为91.0%,预测正确率约为77.7%。
六、随机森林分类
1. 基本原理
集成学习(ensemble learning) 试图通过连续调用单个学习算法,获得不同的模型,然后根据某种规则把这些模型进行组合来解决某一问题,这样做的目的是提高学习系统的泛化能力。组合多个模型预测结果主要采用加权平均或投票的方法。
随机森林(random forest) 是一种常用的集成学习算法,它是将许多棵决策树整合成森林并用来预测最终结果。决策树算法对样本的微小变化会很敏感。在使用分类树进行判别分析时,如果对单个分类树的判别结果不满意,可以考虑随机抽取样本来生成多个分类树,形成一批森林,然后综合森林中的所有树形成最终的单一树的预测结果。这样就能避免单棵树对样本变化敏感的问题,以提高模型的预测能力。
2. R语言实现
set.seed(123)
ctrl<-trainControl(method="repeatedcv",number=10,repeats=3)
rfmodel<-train(type~.,data=data.train,
method="rf",
trControl=ctrl,
tuneLength=5)
varImp(rfmodel)
varImp()函数用来返回各变量的重要程度:
> varImp(rfmodel)
rf variable importance
Overall
glu 100.000
age 46.892
ped 34.886
bmi 29.866
skin 7.340
npreg 6.708
bp 0.000
用图示法显示变量对于模型的重要程度:
library(randomForest)
varImpPlot(rfmodel$finalModel)
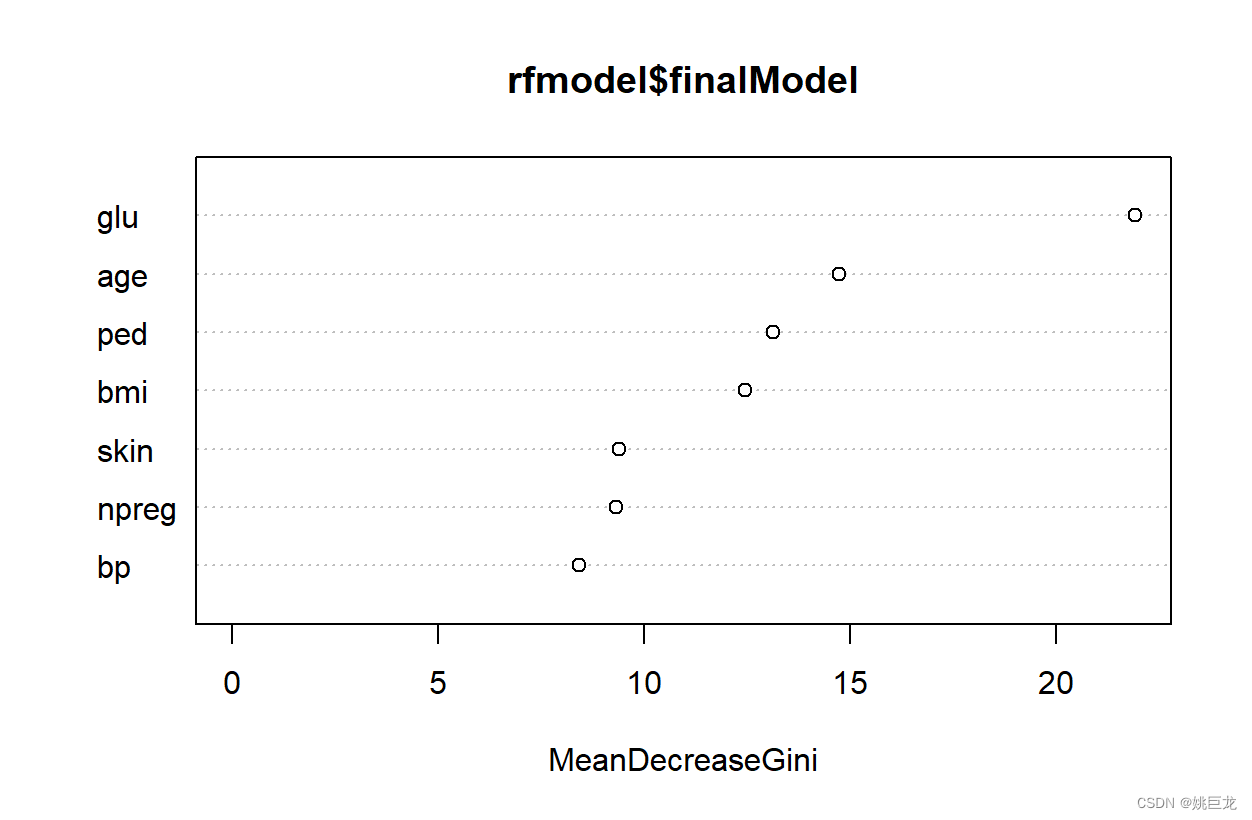
计算回判正确率和预测正确率:
rf.pred.train<-predict.train(rfmodel)
confusionMatrix(rf.pred.train,data.train$type)
rf.pred.test<-predict.train(rfmodel,newdata=data.test[,-8])
confusionMatrix(rf.pred.test,data.test$type)
结果如下:
> confusionMatrix(rf.pred.train,data.train$type)
Confusion Matrix and Statistics
Reference
Prediction No Yes
No 132 0
Yes 0 68
Accuracy : 1
95% CI : (0.9817, 1)
No Information Rate : 0.66
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 1
Mcnemar's Test P-Value : NA
Sensitivity : 1.00
Specificity : 1.00
Pos Pred Value : 1.00
Neg Pred Value : 1.00
Prevalence : 0.66
Detection Rate : 0.66
Detection Prevalence : 0.66
Balanced Accuracy : 1.00
'Positive' Class : No
> confusionMatrix(rf.pred.test,data.test$type)
Confusion Matrix and Statistics
Reference
Prediction No Yes
No 191 44
Yes 32 65
Accuracy : 0.7711
95% CI : (0.7221, 0.8152)
No Information Rate : 0.6717
P-Value [Acc > NIR] : 4.613e-05
Kappa : 0.4659
Mcnemar's Test P-Value : 0.207
Sensitivity : 0.8565
Specificity : 0.5963
Pos Pred Value : 0.8128
Neg Pred Value : 0.6701
Prevalence : 0.6717
Detection Rate : 0.5753
Detection Prevalence : 0.7078
Balanced Accuracy : 0.7264
'Positive' Class : No
回判正确率达到了100%,预测正确率约为77.1%。
七、总结
在选择分类算法时,需要考虑模型的泛化能力、算法复杂度以及对结果的可解释性,且应不断积累新的数据资料,对算法进行修正。
对于以上各类机器学习分类算法的基本原理和推导,有机会再单独做详细的介绍。(留个坑