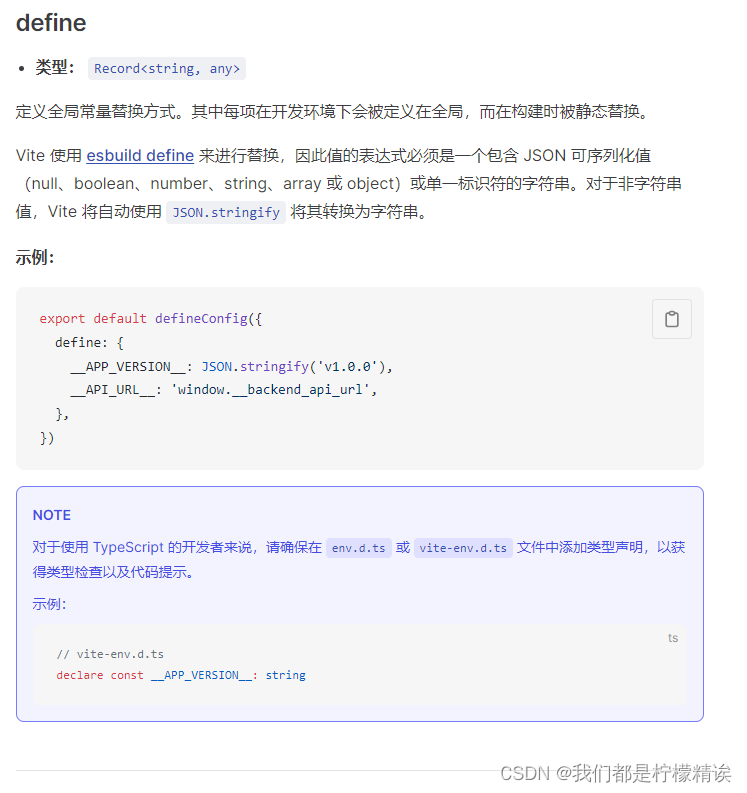
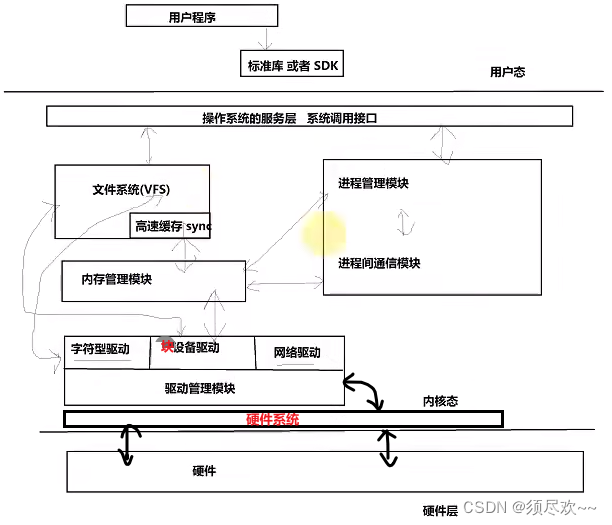
一、 前言
空间划分算法有很多,比如均匀网格,四/八叉树,k-d树,Bsp树,每一种算法都有自己的优缺点,我们需要从理论上理解这些算法,然后在实际项目中进行灵活的运用。
游戏中经常使用空间划分算法来优化碰撞,视锥体剔除,邻近查询,因此每当我们讨论一个算法的时候都会从这三方面进行探讨。另外我们还将考虑静态对象和动态对象对算法的影响,主要体现在空间节点的快速更新能力,以及对象快速变更节点的能力。
二、 均匀网格
我们可以把游戏场景均匀的划分成一个个小的网格如下图:
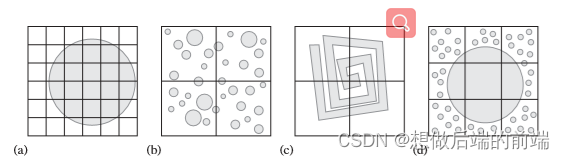
我们先简化讨论的情况,假定:
- 场景对象的坐标是中心位置坐标
- 场景对象的包围盒小于单位网格的尺寸
- 场景对象每帧只做部分对象的碰撞检测
那么碰撞检查只需要在对象中心坐标所属的网格及邻近网格之间进行相交测试,也就是在九宫格中进行碰撞检查。
为什么会得出这个结论呢?大家可以在纸上画一下,因为对象的包围盒小于单位网格,即便它在网格的边界处也无法超出邻近网格的范围。
假定场景被划分成50*50=2500个网格,我们可以根据对象的坐标快速的定位所属及相邻的9个网格。碰撞检测只需要拿出这9个网格中的对象,然后进行相交测试,这样就快速的排除了2491个网格(大部分空间),因此这个算法非常适合碰撞检测及邻近查询。但它对视锥体剔除并不友好,我们需要遍历大量的网格,检测它是否在视锥体中,这个算法并不高效。
对于移动的对象,我们不需要重新划分网格,而且也可以快速的进行网格变更,因此该算法对移动的对象特别友好。
综上所述,均匀网格算法特别适合做碰撞检测及邻近查询,不适合做视锥体剔除,对静态对象及动态对象特别友好。
所有的一切都基于我们之前的假定,但是如果场景中存在比较大的对象,我们就必须扩大单位网格的尺寸,我们希望可以不受对象的限制,合理的分配单位网格的尺寸,如何做到呢?
对大型模型进行切割,用更多小的包围体拆解模型
使用层次网格
ok,我们暂时先不讨论复杂的大型对象,让我们看看均匀网格的实现需要注意哪些问题。
我们需要选择一套数据结构来存储网格及对象,这里要思考静态场景和动态场景的区别,让我们先从简单的静态场景说起。
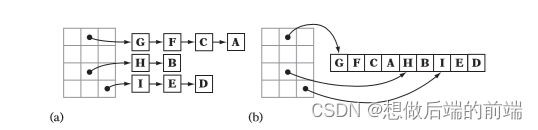
如上图a我们可以用数组下标来代表网格,数组里面存储一个指针,这个指针指向链表的表头。链表中的每一个元素就是网格中的场景对象。这套数据结构不仅可以支持静态场景,还可以支持动态场景,因为随时可以对链表进行增加或删除。但是方案a并不是一个高效的数据结构,因为它用链表来存储对象,会造成内存的浪费,也会降低cpu cache的命中。
方案b用数组取代了链表来存储场景中的对象。数组是一块连续的内存地址,可以提高cpu cache的命中,而且相对于链表可以节省内存空间。每一个网格需要记录存储对象的其实位置,以及所属对象的个数。这需要遍历两次场景第一次确定每个网格的对象数量及对象的总数,第二次遍历分配场景对象。方案b适合静态场景,并且可以离线预处理。
在实际应用中我们往往使用均匀网格处理动态场景,比如MMORPG中管理角色,怪物,npc。
之前介绍的a方案是可以支持动态场景的,但它的效率不高。因为存储对象的数据结构是单向链表,我们插入一个对象的时间复杂度是O(1),查询和删除的时间复杂是O(n)。我们希望查询和删除的时间复杂度也是O(1)。我们可以在对象内部保存链表元素的指针,这样就可以快速的定位元素进行查找和删除操作了。
假设我们的场景很大比如吃鸡游戏,但是场景中的角色数量不多,也就是说场景中大部分网格都是空的,如果为每一个网格分配内存即便是使用数组也是极大的内存浪费。我们希望分配的内存与对象的数量有关和单位网格的尺寸无关(听起来像延迟光照),这就需要请出哈希大神了。我们可以通过一个哈希函数,将网格映射到一个0~n的数组中,如下图:
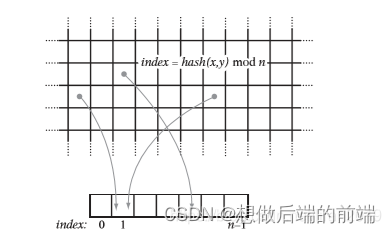
使用哈希表可以大大节省内存空间,但是要解决哈希冲突,如上图有两个网格被分配到了1中。解决哈希冲突又三种方法:
- 开放寻址法
- 再散列法
- 链地址法
之前我们把场景对象都看成是一个点,所以每个对象只存储在一个网格中。如果对象是一个包围盒,那么与包围盒相交的每一个网格都需要存储场景对象。如果包围盒占据44的网格那么它就需要在16个网格中记录对象。这不仅浪费内存空间,还会降低对象插入的速度。为了改善这种情况我们可以按照下图的方式组织对象:
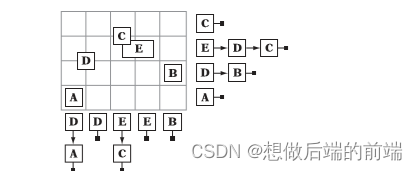
每一个行和列都存储一个链表,这样如果包围盒占据44的网格那么它只需要存储在4+4个网格中。对象的相交测试通过下列方式实现:考查该对象是否与其交叠的行网格单元和列网格单元的其他对象相交。这个方案可以改善最化的插入操作,但是当对象只是与少数网格交叠的时候相交测试的开销反而会变大。
一种较为新颖的存储算法是采用如下方案:针对网格的每一行和每一列及场景对象的数量,分配一个1维数组。
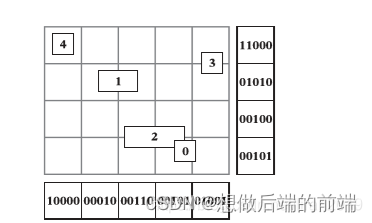
上图中有5个对象,所以每一行和每一列都有一个5位二进制数用来标记它们是否和网格相交。我们看第一行,它与4和3相交,那么第5位和第4位置1。再看第一列,它与4相交,那么第5位置1。我们要想看看第一行第一列的网格中有哪些对象,只需要将行和列的二进制数进行and操作。
11000 & 10000 = 10000,第5位是1其他位是0,说明4号对象在这个网格中(第五位代表4号对象,第一位代表0号对象)。
我们要想获得对象碰撞的潜在集合,只需要看看该对象占用的每一个网格上还有哪些对象,公式如下:
b = (r[i] & c[j]) | (r[i] & c[j+1]) | (r[i+1] & c[j]) | (r[i+1] & c[j+1])
上面的公式可以简化为:
b = (r[i] | r[i+1]) & (c[j] | c[j+1])
我们看看2号对象和哪些对象有可能相交,2号对象占据了3,4行及3,4列。
(00100 | 00101) & (00110 | 00101) = 00101 结果显示第1位和第3位为1,也就是0号对象和3号对象有可能相交。
我能来总结一下每一套数据结构占用内存的大小,如下图:
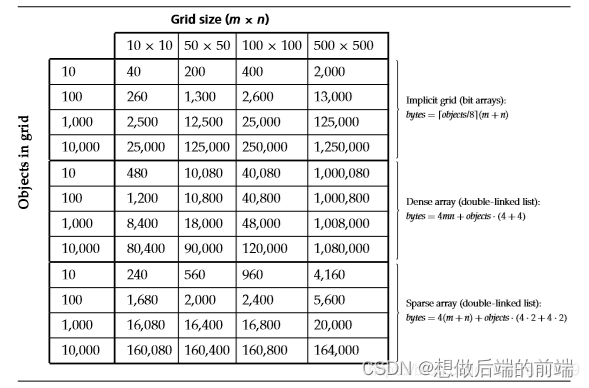
- 第一套是使用位数组,可以看到这套方案大部分情况下占用的内存都是最少的,只有在对象到达10000的时候内存才飙升上来。
- 第二套是紧凑数组+双向链表,可以看到这套数据结构大部分情况下占用的内存都是最高的。
- 第三套是哈希表+双向链表,可以看到这套数据结构的内存占用与对象的数量息息相关,对象数量越多,占用的内存越高。
假定我们在每帧中只测试部分对象
如果我们使用点代表对象,我们需要与所有的邻接网格进行测试,也就是9宫格。
如果我们使用AABB包围盒的最小顶点代表对象,我们可以采用如下算法优化测试:

如果我们用AABB包围盒代表对象,也就是说与AABB相交的网格都包含对象,我们可以使用更快速的测试算法:

最好的情况1次测试,最坏的情况4次测试。虽然加速了碰撞测试的速度,却增大了内存,而且还降低了对象移动更新的效率,因为点的更新速度要比包围盒快很多。所以每一种算法我们都需要根据实际情况进行权衡。
三、 四/八叉树
四叉树理解起来很简单,把蛋糕均匀的切成四份,然后再递归的把每一份切成四份,这样就形成了一棵含有四个子节点的四叉树。八叉树同理就是切成八份。可以想象四/八叉树把空间划分成了很多房间,每个房间中的对象都挂在相应的节点上。递归结束的条件有两种一种是规定树的最大深度,另一种是一直切到每个房间中的对象个数小于某一个阈值。无论是层次网格还是四/八叉树,都会遇到一个问题如下图:

图中灰色的圆球分布在多个网格的交界处,这些圆球到底应该分配到哪个房间中呢?
有两种处理方法一种是每个网格都包含圆球,另一种是把圆球存储到上层节点中。
存储到多个网格的弊端我们之前已经讨论了,把圆球存储到上层节点有什么问题么?如果一个很小的圆球恰好在世界的中心,那么它就会被分配到最上层的根节点。视锥体是无法通过四/八叉树剔除这个圆球的,因为它在最上层的根节点中。同理上面那些灰色的圆球很有可能因为存放在上层空间而无法被剔除,即便它们是很小的物体。这是一个无法彻底解决的问题,但是我们至少让那些小的物体下降到更低的层上,从而让他们能够被正确的剔除。这就需要使用松散四/八叉树。
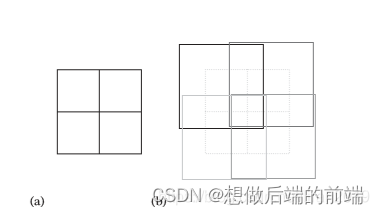
松散四叉树就是适当的扩大每一个网格的尺寸如上图,这样就可以把那些处在边界的小物体囊括到网格中。使用松散四叉树可以让大部分小物体下降到更低的层次,但是有一些真的很大并且在边界的物体依然会被分配到了上层空间中。使用松散四叉树虽然让很多物体下降到了更低的层次,但是空间网格被放大了,如果相机在网格的边缘,原先会被整体剔除的网格现在无法被剔除了,没有完美的结局,只有最适合的结局。
四/八叉树很适合做视锥体剔除,相机可以从根节点遍历树,如果节点被剔除,那么房间中的所有对象都会被剔除。
假定每个对象都被空间节点完全包裹,那么一个房间中的对象就只会和这个房间中的对象发生碰撞,另外处于同一空间中的父子节点也可能发生碰撞。简单的说碰撞检测就是当前节点及父子节点中的对象进行相交测是,这个有点类似层次网格,只是不需要再检测邻接节点了。
让我们来看看八叉树的存储结构,如下图:

节点的中心位置,节点的半径,指向子节点的指针,指向对象的表头指针,这是最简单的八叉树存储结构。如果八叉树是满树,也就是每个节点都包含8个子节点,那么我们也可以使用数组表示八叉树,这种数据结构更紧密。若树节点存储于数组node[N]中,则针对某一父节点node[i],其八叉树的子节点可以表示为node[8i + 1] ~ node[8i + 8]。一个7层的完全八叉树最多包含300000个节点,空间消耗太昂贵了,所以要控制满树的层数,最多不要超过6层。对于动态的八叉树,随着物体的移动八叉树的结构会发生变化,是不是可以直接使用满树来避免树结构的变化,虽然浪费了内存,却换取了计算的时间。
现在高效的做法都是使用哈希存储的线性树,存储结构如下图:、

相对于指针八叉树,每个节点节省了很多内存空间,这些节点会根据key值存储到哈希表中。这样访问节点的速度就从原先的O(logn)变成了O(1)。即节省了内存空间又提升了访问速度,两全其美的优化,吃起来很香。这里神秘的key是什么?它叫Morton code。
Morton order or Morton code map multidimensional data to one dimension while preserving locality of the data points.
莫顿序或莫顿码将多维数据映射到一维,同时保持数据点的局部性。这句话听起来好高大上,让我们用通俗的语言来解释它。
假设我们使用的是四叉树,四叉树中的每一个网格都对应了一个位置坐标(x,y),相当于二维数组的下标,我们把每个节点存储在一个二维数组中,那么根据这组坐标就可以确定节点的位置了。我们希望把这个二维数据(x,y)映射到一维数据中,这就好比将二维数组转换为一维数组,key = x * row_length + y。这里的(x,y)->key,就是morton code前半段话的意思。同时又保持数据节点的局部性这句话怎么解释呢?我们来看一张图

我们可以看到第一张图是一个Z,后面的图都是由Z组成的二维空间,三维空间。这里的局部型就是这个Z,这个曲线也就是Z-order curve曲线。这是感性的认识,让我们理性的看清它的真面目,如下图:
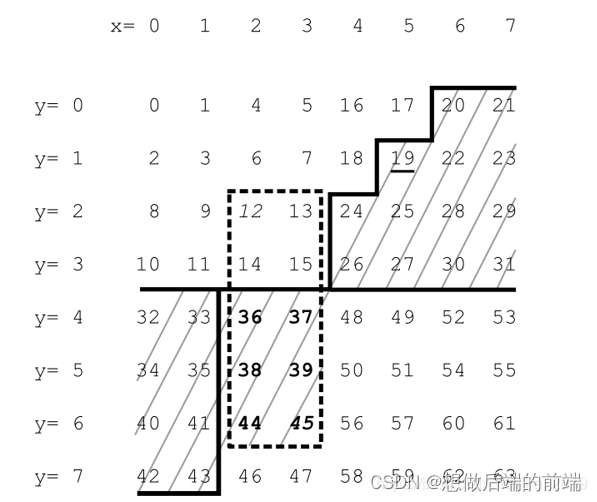
这里有64个节点,相当于四叉树的所有叶子节点。看看0,1,2,3的排列顺序是不是一个Z型,如果0,1,2,3看成是一个点,那么它所属的上层空间(4,5,6,7)(8,9,10,11) (12,13,14,15)组成的是不是也是一个Z型。为什么是Z型不是U型呢。看下面一张图:

我们只需要将x,y的二进制码交替组合就可以得出key值(y是奇数位,x是偶数位)。对于一棵八叉树,我们可以用3位代表子节点的位置(0~7),int是32位,可以代表一个10层的八叉树。为了能够区分011和000011我们需要在前面加上一个1,1011,1000011。这样我们就可以根据key值来计算出这个节点是在第几层,代码如下:

已知父节点的位置码,我们可以方便的计算出子节点的位置码childkey = (parentkey << 3) + childIndex。
已知子节点的位置码我们可以方便的得出父节点的位置码parentkey = childkey >> 3。
我们将位置码做为哈希表的key,这样我们就可以快速的访问八叉树的每一个节点了。
坐标转换 世界坐标->网格坐标(整型)->key。
四、k-d树
k-d树是将k维空间中的点进行分割的数据结构,k代表子划分空间的数量,d是dimension(维度)的意思,k-d树是bsp树的一种,另一种解释是k-d树是二分查找树在k维空间的泛化。
k-d树在一维空间是一棵二分查找树
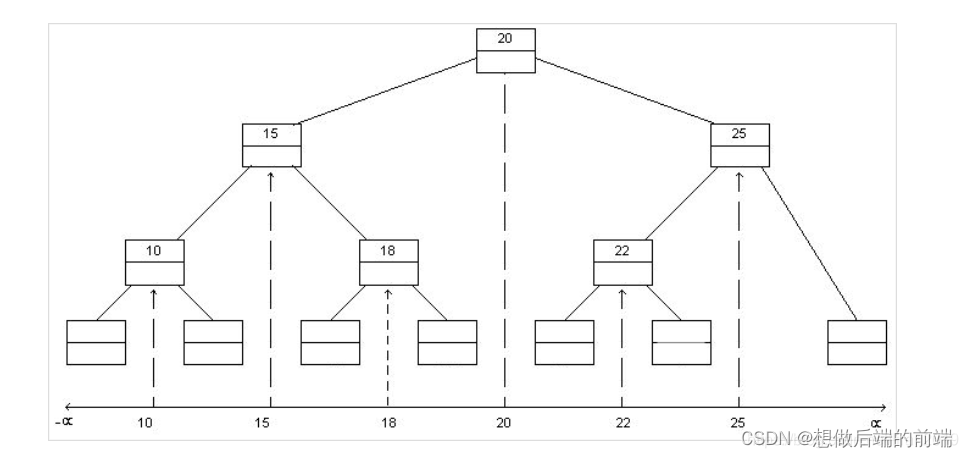
k-d树每次只会选取一个基轴方向进行分割,比如二维空间中先沿x方向分割,然后再沿y轴方向分割,以此循环。
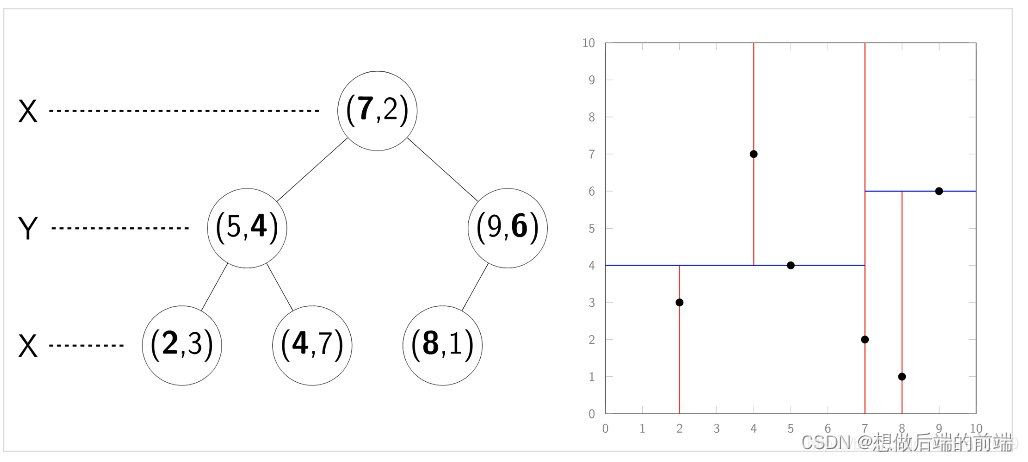
k-d数的建树过程分两步
- 选哪一个轴进行分割
- 沿分割轴方向上的哪个点进行分割
- 将中值左侧的数据挂在左子树,右侧的数据挂在右子树
我们希望构建的树尽量是平衡树而不是一个退化的链表如下图,因此常用的分割策略是
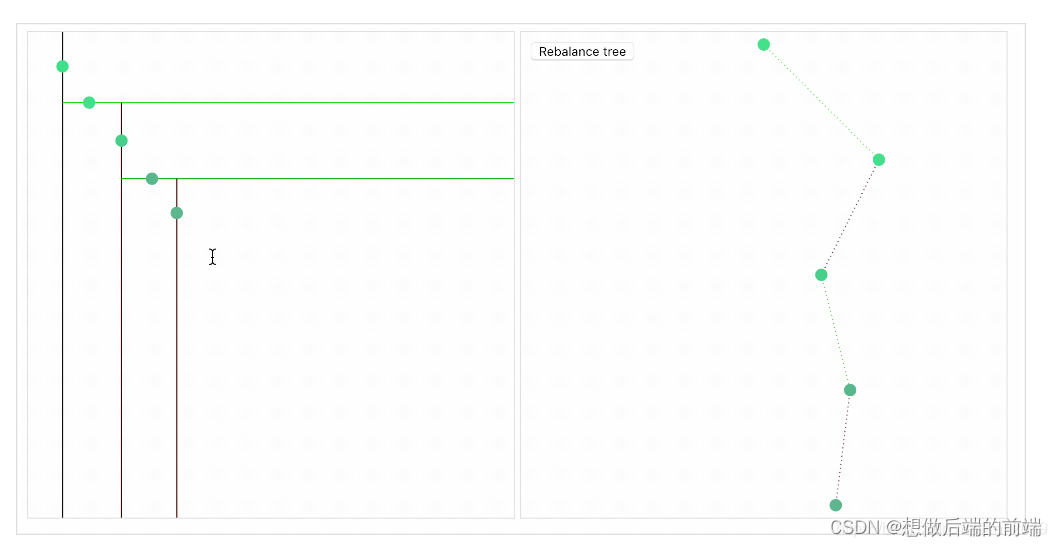
- 对比数据点在各维度的分布情况,数据点在某一维度坐标值的方差越大分布越分散,方差越小分布越集中。从方差大的维度开始切分可以取得很好的切分效果及平衡性。
- 选分割轴上的中值(中间的点)进行分割
k-d树可以做精确查找,也可以做范围查询,当然还可以做视锥体剔除,碰撞检测,确定渲染顺序,因为它也是一棵bsp树。
k-d树最强大的地方是它能对多个维度进行范围查询,比如想要查找年龄在20岁以上并且身高在170到180之间的所有人,用K-D树就能很好的解决。
由于K-D树的结构要求,上面的例子中要求每个人的年龄和身高各项数据必须齐全,如果某个人只有年龄或只有身高,就无法使用K-D树索引了。所以实际上K-D树更常见的应用是经纬度定位,或者三维空间定位(某个维度数据缺失,其他维度数据也就没有意义了)
高纬度数据查找效率并不一定好,有时候可能不如最原始的暴力查找。通常,如果维度为k,则k-d树中的点数N应远远大于2的k次方。否则查找时,节点中大多数节点都会被遍历到,效率上还不如原始的遍历。
说到邻近查询,我们就会和均匀网格进行比较,从查找的效率来看,我个人觉得均匀网格会更快,首先确定附近空间,均匀网格的查找复杂度是O(1)而k-d的复杂度是O(logn),其次动态生成k-d树是非常耗时的,所以k-d树不适合动态场景。k-d树的应用场景更多的应该是在多维度,以及可以是任意数据,比如年龄,身高,体重,财富等等。在游戏中k-d树并不是为了邻近查询,当然它也可以做邻近查询。比如遮挡剔除,需要按照由前到后的顺序渲染,这时候就可以使用k-d树,因为k-d树是bsp树,它可以提供任意视点的渲染顺序。
五、 bsp树
bsp(binary space partitioning )树是所有空间划分中最复杂的一种树形结构,它采用任意位置,方向的分割面递归地将空间划分成多个子空间对。对于n维空间,其分割面则为(n-1)维的超平面。之前说的k-d树就是bsp树的一种,它的划分面是平行于每个轴的面。
bsp树复杂就复杂在它太灵活,一个任意位置,方向的分割面就会让我们不知所措。其实也不是任意的了,每个划分都是为了达到某个目标,这里的任意其实可以理解为手动取选择分割面。(可以参考分离轴定理分割)
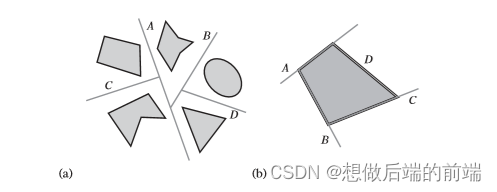
你可以使用bsp树来切割空间如图a,也可以使用bsp树来区分一个复杂多边形的内外区域,如图b。
bsp最初的设计需求是为了对渲染多边形进行排序,参考画家算法,因为当时z-buffer是一个非常昂贵的操作。
bsp的视锥体剔除技术和四/八叉树完全不一样,因此它们一个适合室外,一个适合室内。
四/八叉树的算法决定了它适合广阔的室外场景,而bsp技术则适合有很多房间的室内场景,因为房间中有很多墙,这些墙可以遮挡大片的物体。
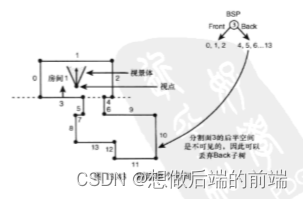
如上图,平面3位于视点的背面,那么3所有的子节点包含的物体都不会被相机看到,这些物体就可以快速的剔除掉。
这就是bsp的背面剔除技术,这里的背面剔除技术不是通过绕序进行裁剪的背面剔除。通过绕序进行裁剪的背面剔除,只需要考虑眼睛的位置,而bsp背面剔除技术需要考虑视点的位置以及视线的朝向还有视锥体的fov。
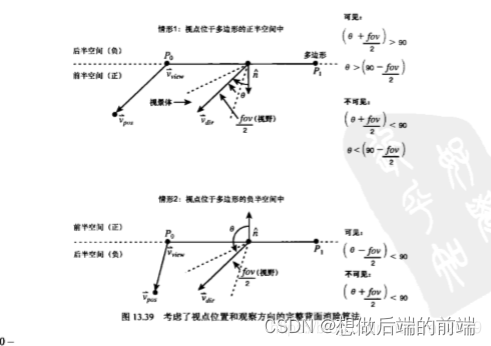
上图是计算背面剔除的方法,我就不详细介绍了,希望了解算法详情的参见《3D游戏大师编程技巧》一书。
做室内游戏,往往需要配一个关卡编辑器,这个编辑器应该有一个功能就是把室内场景中的房间的墙设定成bsp的分割面,然后将场景中的静态物体通过这些分割面生成一棵bsp树。这样就可以进行视锥体剔除了。当然手动设置分割面是一个很低效的做法,自动分割的算法很复杂,需要不停的试探找到一个最优解,因此bsp树通常是在离线预处理。
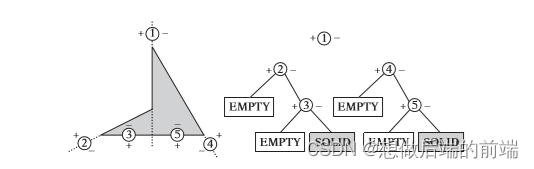
上图是一个凹面体,我们可以使用bsp树来把这个凹面体的内外区域标记出来,一个点从树根处开始遍历,一直找到叶子节点,这样就可以确定这个点是不是在凹面体中了。
bsp树的理论其实并不复杂,复杂在实现上,这里就不更多的介绍了。
六、 混合使用
很多时候我们可以混合使用空间划分算法,比如我们可以先将场景按照均匀网格划分,然后每一个网格再按照树型结构划分,这样就形成了一个森林。再比如我们可以通过均匀网格快速的定位一棵树的节点,这样可以加速树的访问,如下图:
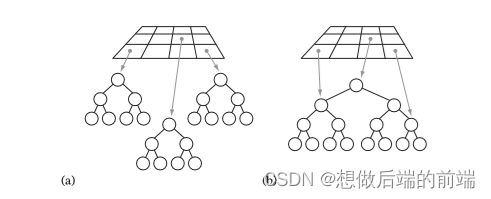
我们假设如果要做GTA5这样的游戏该如何进行场景管理呢?我们先约定一下需求
- GTA5中静态场景非常庞大,场景里面有许多的高楼大厦。
- GTA5里面有许多动态的物体比如汽车,npc而且数量庞大。
再也没有比GTA5更复杂的场景了,我也只是浅浅的做一下个人分析,算是对学习的小结。
- 复杂的城市场景一定要使用遮挡剔除技术,使用遮挡剔除就需要对渲染体进行从前往后的排序。
- 需要一种快速的剔除技术,剔除大量看不见的静态物体。
离线准备工作
- 为场景中的静态物体分配AABB包围盒,一些小的离的近的物体可以分配到一个包围盒中。为场景中所有不透明物体生成一棵k-d树。
- 使用八叉树划分静态场景。
实现
- 使用八叉树进行视锥体剔除,将被剔除的物体进行标记。
- 使用k-d树按照从前往后的顺序遍历场景,首先判断节点是否在视线的背面,如果在背面就剔除这棵子树。如果在前面就遍历节点中所有的包围盒进行遮挡剔除,如果物体已经被视锥体剔除了,那么这个物体就直接跳过。物体通过遮挡剔除后加入到渲染队列中。
- 以主角为中心,使用均匀网格在其周围生成动态的物件,比如行驶的汽车和行人。如果汽车和行人离开一定范围,那么这些动态物件将会被消耗(使用对象缓存技术,防止频繁的gc)。
- 对动态物体进行遮挡查询,之前那些大型的静态物体现在就变成了遮挡体,所以对于动态的物体无需排序,因为它们都是小物件,将测试通过的动态物体加入到渲染队列中。
- 将透明物体加入到渲染队列中。
先用八叉树对物体进行粗粒度剔除,然后再用k-d树进行细粒度剔除,在做遮挡剔除之前,会对物体做视锥体剔除,如果通过视锥体测试,并且通过了遮挡剔除,那么这个物体将会被渲染。对于动态物体我们使用均匀网格控制它们的创建和销毁,没必要整个世界中的动态物体都一直存在。因为动态物体都是小物件,没必要对他们进行排序以进行正确的遮挡剔除,小物件之间的遮挡就没必要测试了。之前的静态物体已经变成了遮挡体,动态物体可以根据这些遮挡体进行剔除。