一、前言

  卷积运算是一种在信号处理、图像处理和神经网络等领域中广泛应用的数学运算。在图像处理和神经网络中，卷积运算可以用来提取特征、模糊图像、边缘检测等。在信号处理中，卷积运算可以用来实现滤波器等操作。

二、实验环境

  本系列实验使用如下环境

conda create -n DL python==3.11

conda activate DL

conda install pytorch torchvision torchaudio pytorch-cuda=12.1 -c pytorch -c nvidia

三、PyTorch数据结构

1、Tensor（张量）

  Tensor（张量）是PyTorch中用于表示多维数据的主要数据结构，类似于多维数组，可以存储和操作数字数据。

1. 维度（Dimensions）

  Tensor（张量）的维度（Dimensions）是指张量的轴数或阶数。在PyTorch中，可以使用size()方法获取张量的维度信息，使用dim()方法获取张量的轴数。

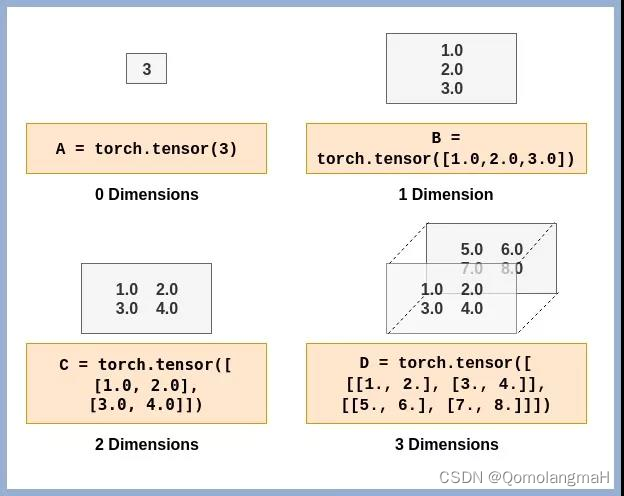
2. 数据类型（Data Types）

  PyTorch中的张量可以具有不同的数据类型：

• torch.float32或torch.float：32位浮点数张量。
• torch.float64或torch.double：64位浮点数张量。
• torch.float16或torch.half：16位浮点数张量。
• torch.int8：8位整数张量。
• torch.int16或torch.short：16位整数张量。
• torch.int32或torch.int：32位整数张量。
• torch.int64或torch.long：64位整数张量。
• torch.bool：布尔张量，存储True或False。

【深度学习】Pytorch 系列教程（一）：PyTorch数据结构：1、Tensor（张量）及其维度（Dimensions）、数据类型（Data Types）

3. GPU加速（GPU Acceleration）

【深度学习】Pytorch 系列教程（二）：PyTorch数据结构：1、Tensor（张量）： GPU加速（GPU Acceleration）

2、张量的数学运算

  PyTorch提供了丰富的操作函数，用于对Tensor进行各种操作，如数学运算、统计计算、张量变形、索引和切片等。这些操作函数能够高效地利用GPU进行并行计算，加速模型训练过程。

1. 向量运算

【深度学习】Pytorch 系列教程（三）：PyTorch数据结构：2、张量的数学运算（1）：向量运算（加减乘除、数乘、内积、外积、范数、广播机制）

2. 矩阵运算

【深度学习】Pytorch 系列教程（四）：PyTorch数据结构：2、张量的数学运算（2）：矩阵运算及其数学原理（基础运算、转置、行列式、迹、伴随矩阵、逆、特征值和特征向量）

3. 向量范数、矩阵范数、与谱半径详解

【深度学习】Pytorch 系列教程（五）：PyTorch数据结构：2、张量的数学运算（3）：向量范数（0、1、2、p、无穷）、矩阵范数（弗罗贝尼乌斯、列和、行和、谱范数、核范数）与谱半径详解

4. 一维卷积运算

  在离散的情况下，给定两个函数$f(n)$和$g(n)$，它们的卷积运算定义为：
$$(f\ast g)(n)=\sum _i(f(i)\cdot g(n-i))$$这里的 $\ast$ 代表卷积运算，$n$ 代表离散的变量。具体地，$f(n)$和$g(n)$的卷积运算$(f\ast g)(n)$表示在$n$位置上的加权求和，其中每个加权项是$f(i)$和$g(n-i)$的乘积，$i$是自由变量。
【深度学习】Pytorch 系列教程（六）：PyTorch数据结构：2、张量的数学运算（4）：一维卷积及其数学原理（步长stride、零填充pad；宽卷积、窄卷积、等宽卷积；卷积运算与互相关运算）

import torch


input_signal = torch.tensor([1, 1, 2, -1, 1, -3, 1], dtype=torch.float)
conv_kernel = torch.tensor([-1, 0, 1], dtype=torch.float)

# 反转卷积核~定义
conv_kernel_flipped = torch.flip(conv_kernel, [0])
K = conv_kernel.numel()
print(f"K:{K}")
# 零填充输入信号
padded_input = torch.nn.functional.pad(input_signal, (K - 1, K - 1), 'constant', 0)
print(f"输入信号:{padded_input}")
# 执行卷积运算
output1 = torch.nn.functional.conv1d(padded_input.view(1, 1, -1), conv_kernel_flipped.view(1, 1, -1))
# 输出结果
print(f"卷积运算:{output1}")
# 互相关运算
output2 = torch.nn.functional.conv1d(padded_input.view(1, 1, -1), conv_kernel.view(1, 1, -1))
# 输出结果
print(f"互相关运算:{output2}")

5. 二维卷积运算

a. 数学原理

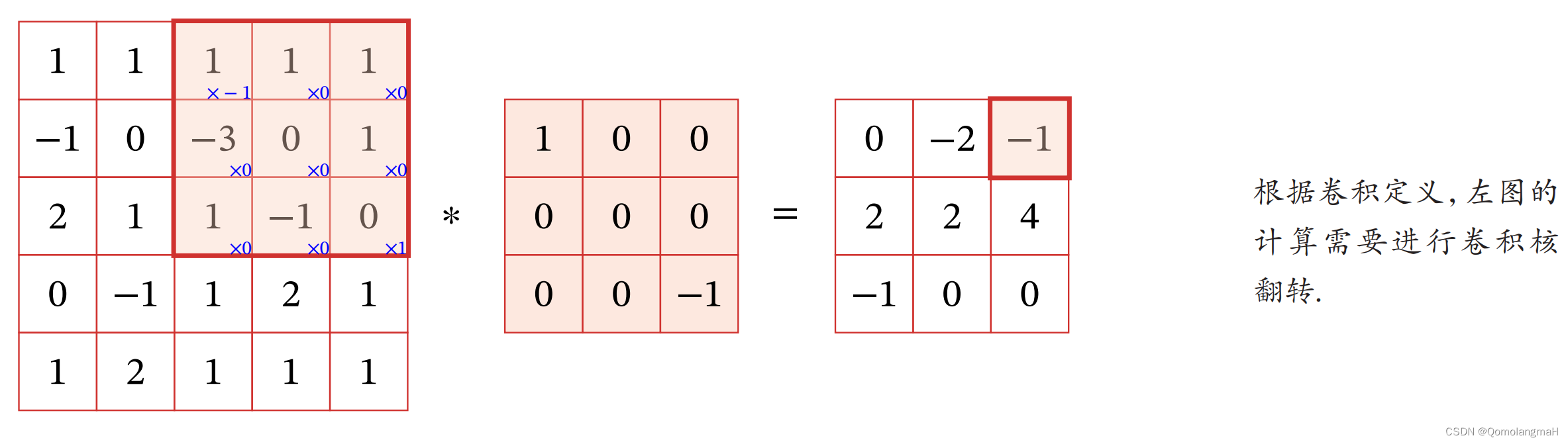
  二维卷积运算是信号处理和图像处理中常用的一种运算方式，当给定两个二维离散信号或图像 $f(x,y)$ 和 $g(x,y)$，其中 $f(x,y)$ 表示输入信号或图像，$g(x,y)$ 表示卷积核。二维卷积运算可以表示为：$$h(x,y)=\sum _m\sum _{n}f(m,n)\cdot g(x-m,y-n)$$其中 ${\sum }_m{\sum }_n$ 表示对所有 $m,n$ 的求和，$h(x,y)$ 表示卷积后的输出信号或图像。

  在数学上，二维卷积运算可以理解为将输入信号或图像 $f(x,y)$ 和卷积核 $g(x,y)$ 进行对应位置的乘法，然后将所有乘积值相加得到输出信号或图像 $h(x,y)$。这个过程可以用于实现一些信号处理和图像处理的操作，例如模糊、边缘检测、图像增强等。
  二维卷积运算在实际应用中有着广泛的应用，如卷积神经网络（CNN）中的卷积层就是利用了二维卷积运算来提取特征。因此，理解二维卷积运算的数学原理对于深度学习和图像处理有着重要的意义。

b. torch.nn.functional.conv2d

import torch
import torch.nn.functional as F


# 一个batch，一个通道，5x5的输入
# 一个通道，3x3的卷积核
input_signal = torch.tensor([[1, 1, 1, 1, 1],
                             [-1, 0, -3, 0, 1],
                             [2, 1, 1, -1, 0],
                             [0, -1, 1, 2, 1],
                             [1, 2, 1, 1, 1]
                             ], dtype=torch.float).view(1, 1, 5, 5)
conv_kernel = torch.tensor([[1, 0, 0],
                            [0, 0, 0],
                            [0, 0, -1]], dtype=torch.float).view(1, 1, 3, 3)
# 反转卷积核~定义
conv_kernel_flipped = torch.flip(conv_kernel, [2, 3])
# 使用conv2d进行卷积运算
# 通过view将形状变为合适的(batch, channel, height, width)
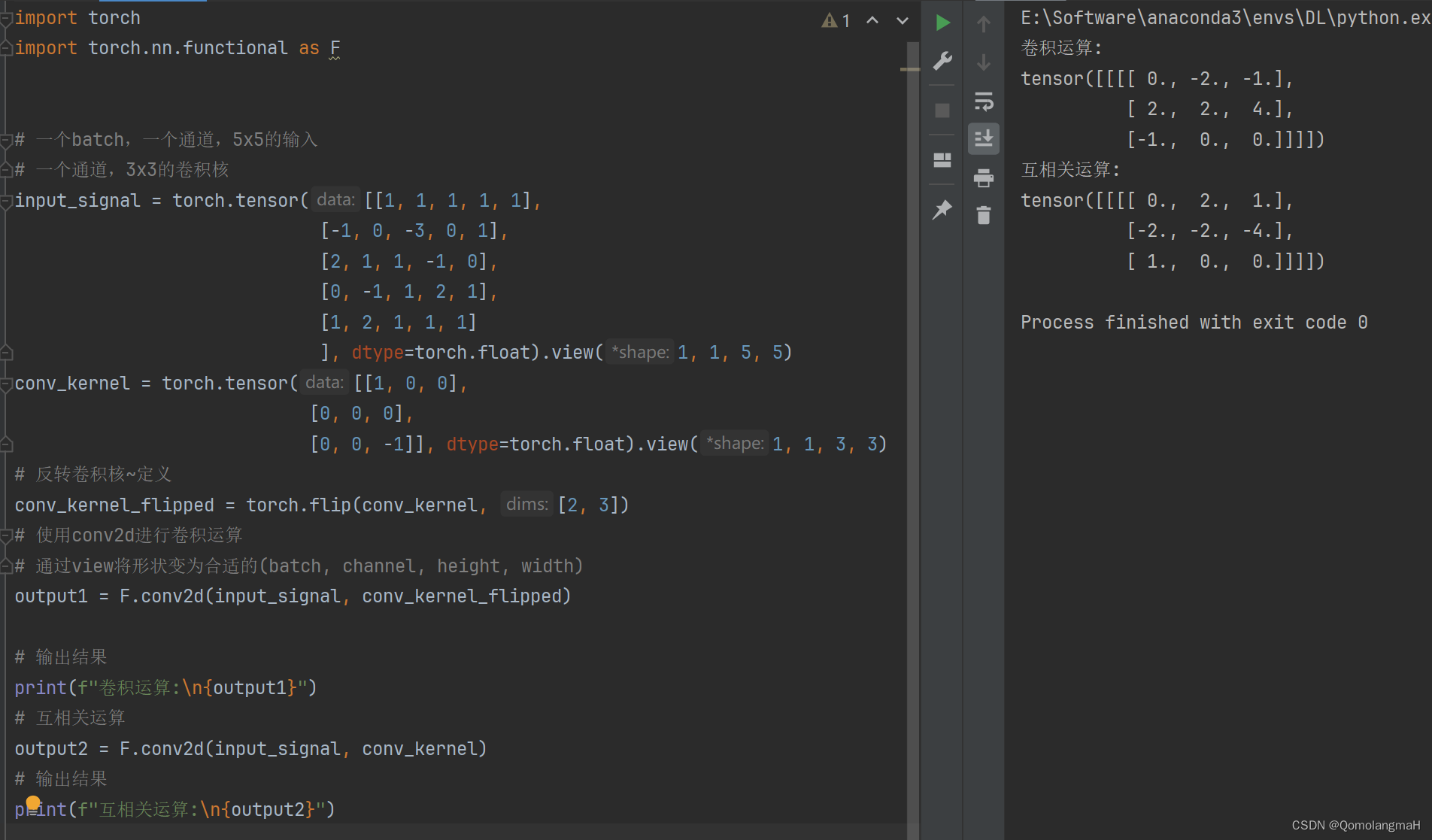
output1 = F.conv2d(input_signal, conv_kernel_flipped)
print(f"卷积运算:\n{output1}")
# 互相关运算
output2 = F.conv2d(input_signal, conv_kernel)
print(f"互相关运算:\n{output2}")

  在 torch.flip 函数中，参数 [2, 3] 指示了在每个维度上进行翻转的操作，[2, 3] 表示对张量的第3维和第4维进行翻转操作。这里卷积核是一个四维张量，第3维表示高度，第4维表示宽度。

c. 步长&零填充

  在卷积的标准定义基础上，还可以引入卷积核的滑动步长和零填充来增加卷积的多样性，可以更灵活地进行特征抽取：

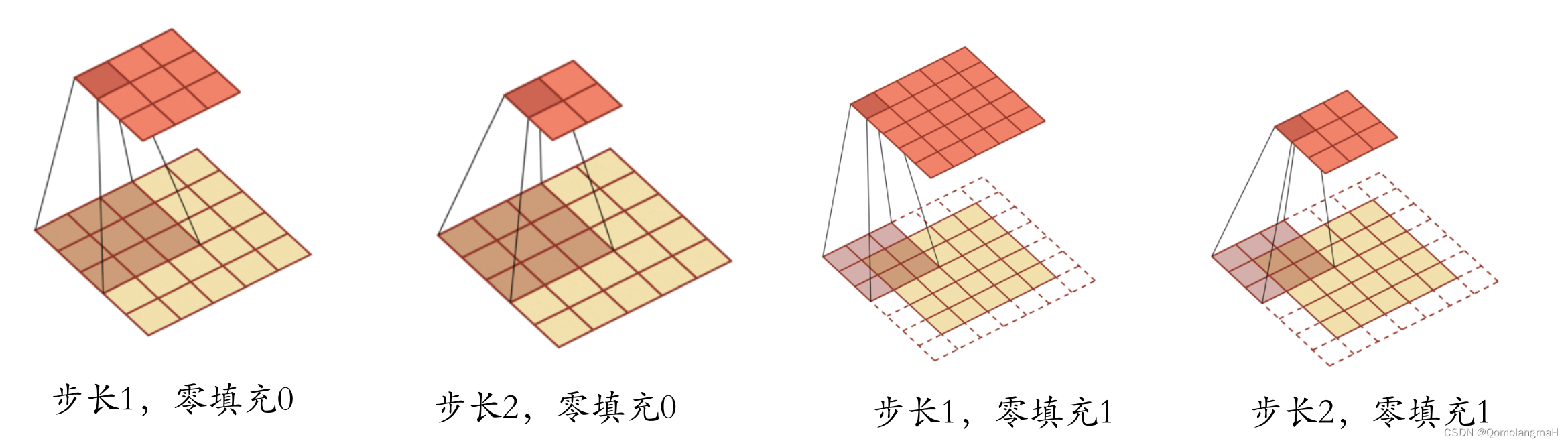
输出形状的计算公式：
  设输入的二维矩阵形状为 $I_H\times I_W$，卷积核形状为 $K_H\times K_W$，步长为 $S$，零填充为 $P$，输出的二维矩阵形状为 $O_H\times O_W$。

则输出矩阵的高度 $O_H$ 和宽度 $O_W$ 可以通过以下公式计算得到：$$O_H=\frac{I_H-K_H+2P}{S}+1$$$$O_W=\frac{I_W-K_W+2P}{S}+1$$

import torch
import torch.nn.functional as F


# 一个batch，一个通道，5x5的输入
# 一个通道，3x3的卷积核
input_signal = torch.tensor([[1, 1, 1, 1, 1],
                             [-1, 0, -3, 0, 1],
                             [2, 1, 1, -1, 0],
                             [0, -1, 1, 2, 1],
                             [1, 2, 1, 1, 1]
                             ], dtype=torch.float).view(1, 1, 5, 5)
conv_kernel = torch.tensor([[1, 0, 0],
                            [0, 0, 0],
                            [0, 0, -1]], dtype=torch.float).view(1, 1, 3, 3)
# 反转卷积核~定义
conv_kernel_flipped = torch.flip(conv_kernel, [2, 3])
# 使用conv2d进行卷积运算
# 通过view将形状变为合适的(batch, channel, height, width)
output1 = F.conv2d(input_signal, conv_kernel_flipped)
print(f"卷积运算:\n{output1}")
# 互相关运算
output2 = F.conv2d(input_signal, conv_kernel)
print(f"互相关运算:\n{output2}")

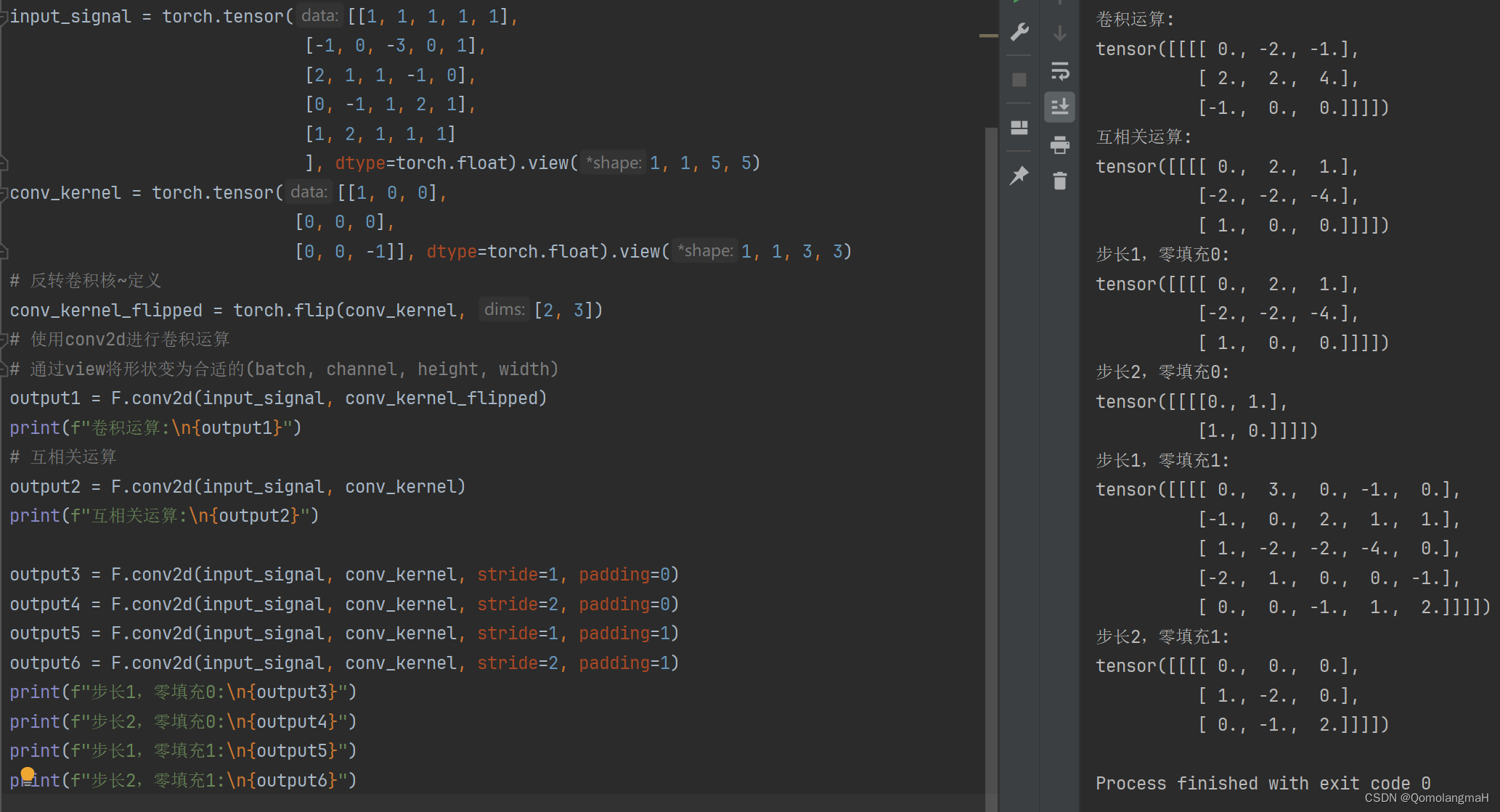
output3 = F.conv2d(input_signal, conv_kernel, stride=1, padding=0)
output4 = F.conv2d(input_signal, conv_kernel, stride=2, padding=0)
output5 = F.conv2d(input_signal, conv_kernel, stride=1, padding=1)
output6 = F.conv2d(input_signal, conv_kernel, stride=2, padding=1)
print(f"步长1，零填充0:\n{output3}")
print(f"步长2，零填充0:\n{output4}")
print(f"步长1，零填充1:\n{output5}")
print(f"步长2，零填充1:\n{output6}")

d. 图像处理~特征提取

  在图像处理中，卷积经常作为特征提取的有效方法．一幅图像在经过卷积操作后得到结果称为特征映射（Feature Map）。图5.3给出在图像处理中几种常用的滤波器，以及其对应的特征映射．图中最上面的滤波器是常用的高斯滤波器，可以用来对图像进行平滑去噪；中间和最下面的滤波器可以用来提取边缘特征。