【leetcode热题】不同的子序列

news2025/1/11 21:09:12

给你两个字符串 s 和 t ，统计并返回在 s 的 子序列 中 t 出现的个数，结果需要对 109 + 7 取模。

示例 1：

输入：s = "rabbbit", t = "rabbit"
输出：3
解释：
如下所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
rabbbit
rabbbit
rabbbit

示例 2：

输入：s = "babgbag", t = "bag"
输出：5
解释：
如下所示, 有 5 种可以从 s 中得到 "bag" 的方案。 
babgbag
babgbag
babgbag
babgbag
babgbag

解法一 递归之分治

S 中的每个字母就是两种可能选他或者不选他。我们用递归的常规思路，将大问题化成小问题，也就是分治的思想。

如果我们求 S[0，S_len - 1] 中能选出多少个 T[0，T_len - 1]，个数记为 n。那么分两种情况，

  • S[0] == T[0]，需要知道两种情况

    • 从 S 中选择当前的字母，此时 S 跳过这个字母, T 也跳过一个字母。

      去求 S[1，S_len - 1] 中能选出多少个 T[1，T_len - 1]，个数记为 n1

    • S 不选当前的字母，此时S跳过这个字母，T 不跳过字母。

      去求S[1，S_len - 1] 中能选出多少个 T[0，T_len - 1]，个数记为 n2

  • S[0] ！= T[0]

    S 只能不选当前的字母，此时S跳过这个字母， T 不跳过字母。

    去求S[1，S_len - 1] 中能选出多少个 T[0，T_len - 1]，个数记为 n1

也就是说如果求 S[0，S_len - 1] 中能选出多少个 T[0，T_len - 1]，个数记为 n。转换为数学式就是

if(S[0] == T[0]){
    n = n1 + n2;
}else{
    n = n1;
}

推广到一般情况，我们可以先写出递归的部分代码。

public int numDistinct(String s, String t) {
    return numDistinctHelper(s, 0, t, 0);
}

private int numDistinctHelper(String s, int s_start, String t, int t_start) {
    int count = 0;
    //当前字母相等
    if (s.charAt(s_start) == t.charAt(t_start)) {
        //从 S 选择当前的字母，此时 S 跳过这个字母, T 也跳过一个字母。
        count = numDistinctHelper(s, s_start + 1, t, t_start + 1, map)
        //S 不选当前的字母，此时 S 跳过这个字母，T 不跳过字母。
                + numDistinctHelper(s, s_start + 1, t, t_start,  map);
    //当前字母不相等  
    }else{ 
       //S 只能不选当前的字母，此时 S 跳过这个字母， T 不跳过字母。
       count = numDistinctHelper(s, s_start + 1, t, t_start,  map);
    }
    return count; 
}

递归出口的话，因为我们的S和T的开始下标都是增长的。

如果S[s_start, S_len - 1]中， s_start 等于了 S_len ，意味着S是空串，从空串中选字符串T，那结果肯定是0。

如果T[t_start, T_len - 1]中，t_start等于了 T_len，意味着T是空串，从S中选择空字符串T，只需要不选择 S 中的所有字母，所以选法是1。

综上，代码总体就是下边的样子

public int numDistinct(String s, String t) {
    return numDistinctHelper(s, 0, t, 0);
}

private int numDistinctHelper(String s, int s_start, String t, int t_start) {
    //T 是空串，选法就是 1 种
    if (t_start == t.length()) { 
        return 1;
    }
    //S 是空串，选法是 0 种
    if (s_start == s.length()) {
        return 0;
    }
    int count = 0;
    //当前字母相等
    if (s.charAt(s_start) == t.charAt(t_start)) {
        //从 S 选择当前的字母，此时 S 跳过这个字母, T 也跳过一个字母。
        count = numDistinctHelper(s, s_start + 1, t, t_start + 1)
        //S 不选当前的字母，此时 S 跳过这个字母，T 不跳过字母。
              + numDistinctHelper(s, s_start + 1, t, t_start);
    //当前字母不相等  
    }else{ 
        //S 只能不选当前的字母，此时 S 跳过这个字母， T 不跳过字母。
        count = numDistinctHelper(s, s_start + 1, t, t_start);
    }
    return count; 
}

遗憾的是，这个解法对于如果S太长的 case 会超时。

原因就是因为递归函数中，我们多次调用了递归函数，这会使得我们重复递归很多的过程，解决方案就很简单了，Memoization 技术，把每次的结果利用一个map保存起来，在求之前，先看map中有没有，有的话直接拿出来就可以了。

map的key的话就标识当前的递归，s_start 和 t_start 联合表示，利用字符串 s_start + '@' + t_start。

value的话就保存这次递归返回的count。

public int numDistinct(String s, String t) {
    HashMap<String, Integer> map = new HashMap<>();
    return numDistinctHelper(s, 0, t, 0, map);
}

private int numDistinctHelper(String s, int s_start, String t, int t_start, HashMap<String, Integer> map) {
    //T 是空串，选法就是 1 种
    if (t_start == t.length()) { 
        return 1;
    }
    //S 是空串，选法是 0 种
    if (s_start == s.length()) {
        return 0;
    }
    String key = s_start + "@" + t_start;
    //先判断之前有没有求过这个解
    if (map.containsKey(key)) {
        return map.get(key); 
    }
    int count = 0;
    //当前字母相等
    if (s.charAt(s_start) == t.charAt(t_start)) {
        //从 S 选择当前的字母，此时 S 跳过这个字母, T 也跳过一个字母。
        count = numDistinctHelper(s, s_start + 1, t, t_start + 1, map)
        //S 不选当前的字母，此时 S 跳过这个字母，T 不跳过字母。
              + numDistinctHelper(s, s_start + 1, t, t_start, map);
    //当前字母不相等  
    }else{ 
        //S 只能不选当前的字母，此时 S 跳过这个字母， T 不跳过字母。
        count = numDistinctHelper(s, s_start + 1, t, t_start, map);
    }
    //将当前解放到 map 中
    map.put(key, count);
    return count; 
}

解法二 递归之回溯

回溯的思想就是朝着一个方向找到一个解，然后再回到之前的状态，改变当前状态，继续尝试得到新的解。可以类比于二叉树的DFS，一路走到底，然后回到之前的节点继续递归。

对于这道题，和二叉树的DFS很像了，每次有两个可选的状态，选择S串的当前字母和不选择当前字母。

当S串的当前字母和T串的当前字母相等，我们就可以选择S的当前字母，进入递归。

递归出来以后，继续尝试不选择S的当前字母，进入递归。

代码可以是下边这样。

public int numDistinct3(String s, String t) { 
    numDistinctHelper(s, 0, t, 0);
}

private void numDistinctHelper(String s, int s_start, String t, int t_start) {
    //当前字母相等，选中当前 S 的字母，s_start 后移一个
    //选中当前 S 的字母，意味着和 T 的当前字母匹配，所以 t_start 后移一个
    if (s.charAt(s_start) == t.charAt(t_start)) {
        numDistinctHelper(s, s_start + 1, t, t_start + 1);
    }
    //出来以后，继续尝试不选择当前字母，s_start 后移一个，t_start 不后移
    numDistinctHelper(s, s_start + 1, t, t_start);
}

递归出口的话，就是两种了。

  • 当t_start == T_len，那么就意味着当前从S中选择的字母组成了T，此时就代表一种选法。我们可以用一个全局变量count，count计数此时就加一。然后return，返回到上一层继续寻求解。

  • 当s_start == S_len，此时S到达了结尾，直接 return。

int count = 0;
public int numDistinct(String s, String t) { 
    numDistinctHelper(s, 0, t, 0);
    return count;
}

private void numDistinctHelper(String s, int s_start, String t, int t_start) {
    if (t_start == t.length()) {
        count++; 
        return;
    }
    if (s_start == s.length()) {
        return;
    }
    //当前字母相等，s_start 后移一个，t_start 后移一个
    if (s.charAt(s_start) == t.charAt(t_start)) {
        numDistinctHelper(s, s_start + 1, t, t_start + 1);
    }
    //出来以后，继续尝试不选择当前字母，s_start 后移一个，t_start 不后移
    numDistinctHelper(s, s_start + 1, t, t_start);
}

好吧，这个熟悉的错误又出现了，同样是递归中调用了两次递归，会重复计算一些解。怎么办呢？Memoization 技术。

map的key和之前一样，标识当前的递归，s_start 和 t_start 联合表示，利用字符串 s_start + '@' + t_start。

map的value的话？存什么呢。区别于解法一，我们每次都得到了当前条件下的count，然后存起来了。而现在我们只有一个全局变量，该怎么办呢？存全局变量count吗？

如果递归过程中

if (map.containsKey(key)) {
   ... ...
}

遇到了已经求过的解该怎么办呢？

我们每次得到一个解后增加全局变量count，所以我们map的value存两次递归后 count 的增量。这样的话，第二次遇到同样的情况的时候，就不用递归了，把当前增量加上就可以了。

if (map.containsKey(key)) {
    count += map.get(key);
    return; 
}

综上，代码就出来了

int count = 0;
public int numDistinct(String s, String t) { 
    HashMap<String, Integer> map = new HashMap<>();
    numDistinctHelper(s, 0, t, 0, map);
    return count;
}

private void numDistinctHelper(String s, int s_start, String t, int t_start, 
            HashMap<String, Integer> map) {
    if (t_start == t.length()) {
        count++; 
        return;
    }
    if (s_start == s.length()) {
        return;
    }
    String key = s_start + "@" + t_start;
    if (map.containsKey(key)) {
        count += map.get(key);
        return; 
    }
    int count_pre = count;
    //当前字母相等，s_start 后移一个，t_start 后移一个
    if (s.charAt(s_start) == t.charAt(t_start)) {
        numDistinctHelper(s, s_start + 1, t, t_start + 1, map);
    }
    //出来以后，继续尝试不选择当前字母，s_start 后移一个，t_start 不后移
    numDistinctHelper(s, s_start + 1, t, t_start, map);

    //将增量存起来
    int count_increment = count - count_pre;
    map.put(key, count_increment); 
}

解法三 动态规划

让我们来回想一下解法一做了什么。s_start 和 t_start 不停的增加，一直压栈，压栈，直到

//T 是空串，选法就是 1 种
if (t_start == t.length()) { 
    return 1;
}
//S 是空串，选法是 0 种
if (s_start == s.length()) {
    return 0;
}

T 是空串或者 S 是空串，我们就直接可以返回结果了，接下来就是不停的出栈出栈，然后把结果通过递推关系取得。

递归的过程就是由顶到底再回到顶。

动态规划要做的就是去省略压栈的过程，直接由底向顶。

这里我们用一个二维数组 dp[m][n] 对应于从 S[m，S_len) 中能选出多少个 T[n，T_len)。

当 m == S_len，意味着S是空串，此时dp[S_len][n]，n 取 0 到 T_len - 1的值都为 0。

当 n == T_len，意味着T是空串，此时dp[m][T_len]，m 取 0 到 S_len的值都为 1。

然后状态转移的话和解法一分析的一样。如果求dp[s][t]。

  • S[s] == T[t]，当前字符相等，那就对应两种情况，选择S的当前字母和不选择S的当前字母

    dp[s][t] = dp[s+1][t+1] + dp[s+1][t]

  • S[s] != T[t]，只有一种情况，不选择S的当前字母

    dp[s][t] = dp[s+1][t]

代码就可以写了。

public int numDistinct(String s, String t) {
    int s_len = s.length();
    int t_len = t.length();
    int[][] dp = new int[s_len + 1][t_len + 1];
    //当 T 为空串时，所有的 s 对应于 1
    for (int i = 0; i <= s_len; i++) {
        dp[i][t_len] = 1;
    }

    //倒着进行，T 每次增加一个字母
    for (int t_i = t_len - 1; t_i >= 0; t_i--) {
        dp[s_len][t_i] = 0; // 这句可以省去，因为默认值是 0
        //倒着进行，S 每次增加一个字母
        for (int s_i = s_len - 1; s_i >= 0; s_i--) {
            //如果当前字母相等
            if (t.charAt(t_i) == s.charAt(s_i)) {
                //对应于两种情况，选择当前字母和不选择当前字母
                dp[s_i][t_i] = dp[s_i + 1][t_i + 1] + dp[s_i + 1][t_i];
            //如果当前字母不相等
            } else {
                dp[s_i][t_i] = dp[s_i + 1][t_i];
            }
        }
    }
    return dp[0][0];
}

对比于解法一和解法二，如果Memoization 技术我们不用hash，而是用一个二维数组，会发现其实我们的递归过程，其实就是在更新下图中的二维表，只不过更新的顺序没有动态规划这么归整。这也是不用Memoization 技术会超时的原因，如果把递归的更新路线画出来，会发现很多路线重合了，意味着我们进行了很多没有必要的递归，从而造成了超时。

我们画一下动态规划的过程。

S = "babgbag", T = "bag"

T 为空串时，所有的 s 对应于 1。 S 为空串时，所有的 t 对应于 0。

此时我们从 dp[6][2] 开始求。根据公式，因为当前字母相等，所以 dp[6][2] = dp[7][3] + dp[7][2] = 1 + 0 = 1 。

接着求dp[5][2]，当前字母不相等，dp[5][2] = dp[6][2] = 1。

一直求下去。

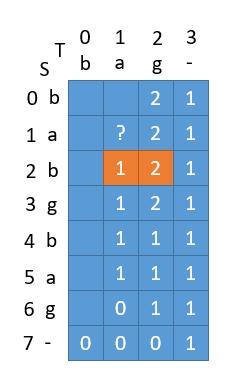
求当前问号的地方的值的时候，我们只需要它的上一个值和斜对角的值。

换句话讲，求当前列的时候，我们只需要上一列的信息。比如当前求第1列，第3列的值就不会用到了。

所以我们可以优化算法的空间复杂度，不需要二维数组，需要一维数组就够了。

此时需要解决一个问题，就是当求上图的dp[1][1]的时候，需要dp[2][1]和dp[2][2]的信息。但是如果我们是一维数组，dp[2][1]之前已经把dp[2][2]的信息覆盖掉了。所以我们需要一个pre变量保存之前的值。

public int numDistinct(String s, String t) {
    int s_len = s.length();
    int t_len = t.length();
    int[]dp = new int[s_len + 1];
    for (int i = 0; i <= s_len; i++) {
        dp[i] = 1;
    }
  //倒着进行，T 每次增加一个字母
    for (int t_i = t_len - 1; t_i >= 0; t_i--) {
        int pre = dp[s_len];
        dp[s_len] = 0; 
         //倒着进行，S 每次增加一个字母
        for (int s_i = s_len - 1; s_i >= 0; s_i--) {
            int temp = dp[s_i];
            if (t.charAt(t_i) == s.charAt(s_i)) {
                dp[s_i] = dp[s_i + 1] + pre;
            } else {
                dp[s_i] = dp[s_i + 1];
            }
            pre = temp;
        }
    }
    return dp[0];
}

利用temp和pre两个变量实现了保存之前的值。

其实动态规划优化空间复杂度的思想，在 5题，10题，53题，72题 等等都已经用了，是非常经典的。

上边的动态规划是从字符串末尾倒着进行的，其实我们只要改变dp数组的含义，用dp[m][n]表示S[0,m)和T[0,n)，然后两层循环我们就可以从 1 往末尾进行了，思想是类似的，leetcode 高票答案也都是这样的，如果理解了上边的思想，代码其实也很好写。这里只分享下代码吧。

public int numDistinct(String s, String t) {
    int s_len = s.length();
    int t_len = t.length();
    int[] dp = new int[s_len + 1];
    for (int i = 0; i <= s_len; i++) {
        dp[i] = 1;
    }
    for (int t_i = 1; t_i <= t_len; t_i++) {
        int pre = dp[0];
        dp[0] = 0;
        for (int s_i = 1; s_i <= s_len; s_i++) {
            int temp = dp[s_i];
            if (t.charAt(t_i - 1) == s.charAt(s_i - 1)) {
                dp[s_i] = dp[s_i - 1] + pre;
            } else {
                dp[s_i] = dp[s_i - 1];
            }
            pre = temp;
        }
    }
    return dp[s_len];
}

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1466746.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

挑战杯 基于大数据的时间序列股价预测分析与可视化 - lstm

挑战杯 基于大数据的时间序列股价预测分析与可视化 - lstm

文章目录 1 前言2 时间序列的由来2.1 四种模型的名称&#xff1a; 3 数据预览4 理论公式4.1 协方差4.2 相关系数4.3 scikit-learn计算相关性 5 金融数据的时序分析5.1 数据概况5.2 序列变化情况计算 最后 1 前言 &#x1f525; 优质竞赛项目系列&#xff0c;今天要分享的是 &…
阅读更多...
K8S-001-Virtual box - Network Config

K8S-001-Virtual box - Network Config

A. 配置两个IP&#xff0c; 一个连接内网&#xff0c;一个链接外网: 1. 内网配置(Host only&#xff0c; 不同的 virutal box 的版本可以不一样&#xff0c;这些窗口可能在不同的地方&#xff0c;但是配置的内容是一样的): 静态IP 动态IP 2. 外网&#xff08;创建一个 Networ…
阅读更多...
网络安全笔记总结

网络安全笔记总结

IAE引擎 1.深度检测技术--DFI和DPI技术 DFI和DPI都是流量解析技术&#xff0c;对业务的应用、行为及具体信息进行识别&#xff0c;主要应用于流量分析及流量检测。 DPI&#xff1a;深度包检测技术 DPI是一种基于应用层的流量检测和控制技术&#xff0c;对流量进行拆包&#x…
阅读更多...
信号系统之傅里叶变换属性

信号系统之傅里叶变换属性

1 傅里叶变换的线性度 傅里叶变换是线性的&#xff0c;即具有均匀性和可加性的性质。对于傅里叶变换家族的所有四个成员&#xff08;傅里叶变换、傅里叶级数、DFT 和 DTFT&#xff09;都是如此。 图 10-1 提供了一个示例&#xff0c;说明均匀性如何成为傅里叶变换的一个属性。…
阅读更多...
第八篇【传奇开心果系列】python的文本和语音相互转换库技术点案例示例：Google Text-to-Speech虚拟现实（VR）沉浸式体验经典案例

第八篇【传奇开心果系列】python的文本和语音相互转换库技术点案例示例：Google Text-to-Speech虚拟现实（VR）沉浸式体验经典案例

传奇开心果博文系列 系列博文目录python的文本和语音相互转换库技术点案例示例系列 博文目录前言一、雏形示例代码二、扩展思路介绍三、虚拟导游示例代码四、交互式学习示例代码五、虚拟角色对话示例代码六、辅助用户界面示例代码七、实时语音交互示例代码八、多语言支持示例代…
阅读更多...
vue 手势解锁功能

vue 手势解锁功能

效果 实现 <script setup lang"ts"> const canvasRef ref<HTMLCanvasElement>() const ctx ref<CanvasRenderingContext2D | null>(null) const width px2px(600) const height px2px(700) const radius ref(px2px(50))const init () > …
阅读更多...
Java面试问题集锦

Java面试问题集锦

1.JDK、JRE、JVM 三者有什么关系&#xff1f; JDK&#xff08;全称 Java Development Kit&#xff09;&#xff0c;Java开发工具包&#xff0c;能独立创建、编译、运行程序。 JDK JRE java开发工具&#xff08;javac.exe/java.exe/jar.exe) JRE&#xff08;全称 Java Runtim…
阅读更多...
MyBatis之Mapper.xml文件中parameterType，resultType，resultMap的用法

MyBatis之Mapper.xml文件中parameterType，resultType，resultMap的用法

MyBatis之自定义数据类型转换器 前言1.parameterType2.resultType3.resultMap实例代码总结 前言 今天我们来学习Mapper.xml&#xff08;编写SQL的&#xff09;文件中&#xff0c;增删改查标签中&#xff0c;使用parameterType属性指定传递参数类型&#xff0c;resultType属性指…
阅读更多...
C# OpenCvSharp 利用白平衡技术进行图像修复

C# OpenCvSharp 利用白平衡技术进行图像修复

目录 效果 灰度世界(GrayworldWB)-白平衡算法 完美反射(SimpleWB)-白平衡算法 基于学习的(LearningBasedWB)-白平衡算法 代码 下载 C# OpenCvSharp 利用白平衡技术进行图像修复 OpenCV xphoto模块中提供了三种不同的白平衡算法&#xff0c;分别是&#xff1a;灰度世界(G…
阅读更多...
Linux进一步研究权限-----------ACL使用

Linux进一步研究权限-----------ACL使用

一、使用情况 1.1、场景: 某个大公司&#xff0c;在一个部门&#xff0c;有一个经理和手下有两个员工&#xff0c;在操控一个Linux项目,项目又分为三期做&#xff0c;然而一期比较重要&#xff0c;经理带着员工做完了&#xff0c;公司就觉得技术难点已经做完攻克了&#xff0…
阅读更多...
npm install报错解决记录

npm install报错解决记录

npm install报错解决记录 常见错误类型 权限错误: EACCES: permission denied EPERM: operation not permitted网络错误: ECONNREFUSED: Connection refused ETIMEDOUT: connect ETIMEDOUT包解析错误: Cannot find module ‘xxx’ Error: No compatible version found编译错误…
阅读更多...
飞行机器人专栏（十三）-- 智能优化算法之粒子群优化算法与多目标优化

飞行机器人专栏（十三）-- 智能优化算法之粒子群优化算法与多目标优化

一、理论基础 1.1 引言 粒子群优化算法&#xff08;Particle Swarm Optimization, PSO&#xff09;自1995年由Eberhart和Kennedy提出以来&#xff0c;已经成为解决优化问题的一种有效且广泛应用的方法。作为一种进化计算技术&#xff0c;PSO受到社会行为模式&#xff0c;特别是…
阅读更多...
互联设备-中继器-路由器等

互联设备-中继器-路由器等

网卡的主要作用 1 在发送方 把从计算机系统要发送的数据转换成能在网线上传输的bit 流 。 2 在接收方 把从网线上接收来的 bit 流重组成计算机系统可以 处理的数据 。 3 判断数据是否是发给自己的 4 发送和控制计算机系统和网线数据流 计算机的分类 1、台式机 2、小型机和服…
阅读更多...
【DDD】学习笔记-薪资管理系统的测试驱动开发

【DDD】学习笔记-薪资管理系统的测试驱动开发

回顾薪资管理系统的设计建模 在 3-15 课&#xff0c;我们通过场景驱动设计完成了薪资管理系统的领域设计建模。既然场景驱动设计可以很好地与测试驱动开发融合在一起&#xff0c;因此根据场景驱动设计的成果来开展测试驱动开发&#xff0c;就是一个水到渠成的过程。让我们先来…
阅读更多...
rem适配方案

rem适配方案

目录 一&#xff0c;rem实际开发适配方案 二&#xff0c;rem适配方案技术使用&#xff08;市场主流&#xff09; 方案一&#xff1a; 方案二&#xff1a;​编辑 一&#xff0c;rem实际开发适配方案 ① 按照设计稿与设备宽度的比例&#xff0c;动态计算并设置html根标签的fo…
阅读更多...
【自然语言处理-二-attention注意力 是什么】

【自然语言处理-二-attention注意力 是什么】

自然语言处理二-attention 注意力机制 自然语言处理二-attention 注意力记忆能力回顾下RNN&#xff08;也包括LSTM GRU&#xff09;解决memory问题改进后基于attention注意力的modelmatch操作softmax操作softmax值与hidder layer的值做weight sum 计算和将计算出来的和作为memo…
阅读更多...
Jetpack Compose 架构层

Jetpack Compose 架构层

点击查看&#xff1a;Jetpack Compose 架构层 官网 本页面简要介绍了组成 Jetpack Compose 的架构层&#xff0c;以及这种设计所依据的核心原则。 Jetpack Compose 不是一个单体式项目&#xff1b;它由一些模块构建而成&#xff0c;这些模块组合在一起&#xff0c;构成了一个完…
阅读更多...
基于YOLOv8/YOLOv7/YOLOv6/YOLOv5的人脸表情识别系统（附完整资源+PySide6界面+训练代码）

基于YOLOv8/YOLOv7/YOLOv6/YOLOv5的人脸表情识别系统（附完整资源+PySide6界面+训练代码）

摘要&#xff1a;本篇博客呈现了一种基于深度学习的人脸表情识别系统&#xff0c;并详细展示了其实现代码。系统采纳了领先的YOLOv8算法&#xff0c;并与YOLOv7、YOLOv6、YOLOv5等早期版本进行了比较&#xff0c;展示了其在图像、视频、实时视频流及批量文件中识别人脸表情的高…
阅读更多...
【elementUi-table表格】 滚动条 新增监听事件； 滚动条滑动到指定位置；

【elementUi-table表格】 滚动条 新增监听事件； 滚动条滑动到指定位置；

1、给滚动条增加监听 this.dom this.$refs.tableRef.bodyWrapperthis.dom.scrollTop 0let _that thisthis.dom.addEventListener(scroll, () > {//获取元素的滚动距离let scrollTop _that.dom.scrollTop//获取元素可视区域的高度let clientHeight this.dom.clientHeigh…
阅读更多...
springboot+vue项目基础开发(17)路由使用

springboot+vue项目基础开发(17)路由使用

路由 在前端中，路由指的是根据不同的访问路径，展示不同的内容 vue Router的vue.js的官方路由 安装vue Router 再启动 在src下面新建router文件,创建index.js 代码 import {createRouter,createWebHashHistory} from vue-router //导入组件 import Login from @/views/Log…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023