891. 子序列宽度之和

一个序列的 宽度 定义为该序列中最大元素和最小元素的差值。

给你一个整数数组 nums ，返回 nums 的所有非空 子序列 的 宽度之和 。由于答案可能非常大，请返回对 109 + 7 取余 后的结果。

子序列 定义为从一个数组里删除一些（或者不删除）元素，但不改变剩下元素的顺序得到的数组。例如，[3,6,2,7] 就是数组 [0,3,1,6,2,2,7] 的一个子序列。

示例 1：

输入：nums = [2,1,3]
输出：6
解释：子序列为 [1], [2], [3], [2,1], [2,3], [1,3], [2,1,3] 。
相应的宽度是 0, 0, 0, 1, 1, 2, 2 。 宽度之和是 6 。

示例 2：

输入：nums = [2]
输出：0

提示：

1 <= nums.length <= 1e5
1 <= nums[i] <= 1e5

解析：

• 方法1，我们可以根据长度暴力枚举每个子序列，然后找出每个子序列的最大值最小值，这种思考方法属于，子序列为主，在考虑最大最小值。
• 显然，方法1不适合。我们可以转换思考角度，可以先针对每个元素考虑，枚举每个元素作为最大值最小值的情况，然后再考虑这个元素作为最大值或者最小值能出现在多少个子序列中。
• 然后，计算每个元素的贡献值。如果 a 元素作为最大值出现在10个子序列中，那么贡献值为 10a，如果作为最小值出现在20个子序列中那么贡献值为 -20a 。就这样计算出所有元素的贡献值之和。
• 怎样计算每个元素作为最大最小出现再多少个子序列中呢？
• 例如：1 2 4 3，
• 1作为最小值会出现在2 4 3这三个元素任意组成的子序列中（不考虑顺序问题）；
• 2作为最小值会出现4，3组成的子序列中；
• …
• 1作为最大值会出现在 1 组成的子序列中；
• 2作为最大值会出现在1 2组成的子序列中；
• 3作为最大值会出现在1 2 3组成的子序列中；
• 可以发现，每个元素作为最大值的子序列个数，是由比他小的元素组成；每个元素作为最小值的子序列个数，是由比他大的元素组成；因此，只需要统计每个元素的较小，较大元素个数（排序），然后再根据元素个数计算元素组合个数即可。
• 怎么计算元素组合个数 ? f[i]表示i个元素的组合数

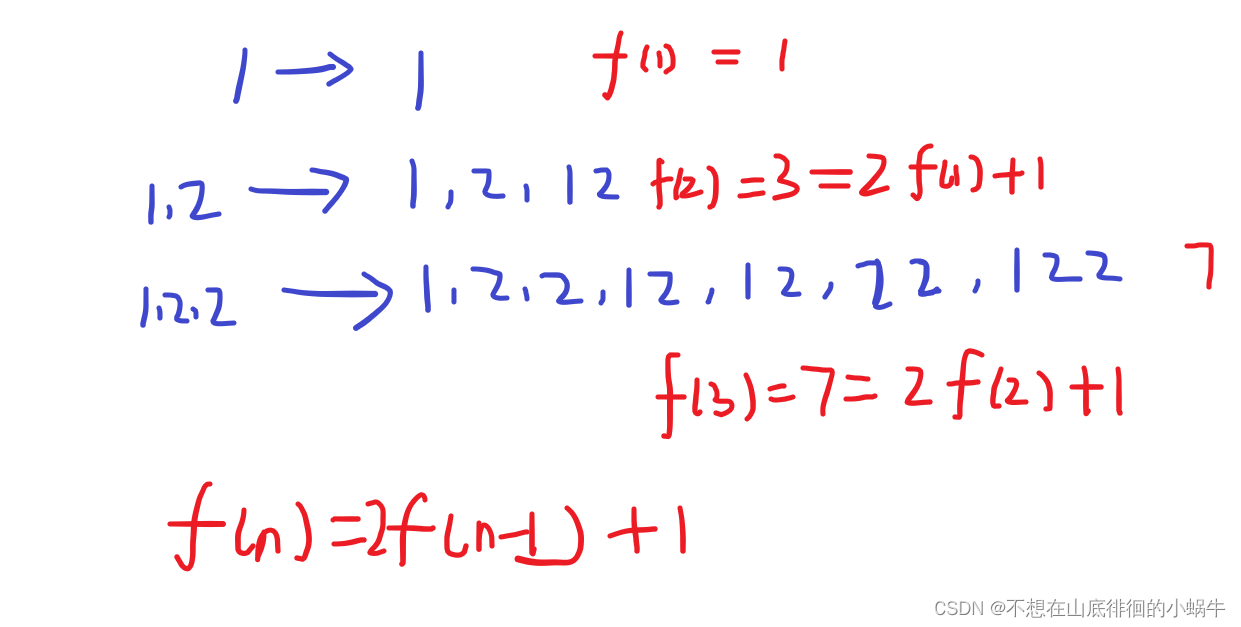
总结：子序列问题+不依赖相对位置（不考虑顺序）==》 不需要保留原有位置 ==》可以排序。

代码：

class Solution {
    int mod=1e9+7;
public:
    int sumSubseqWidths(vector<int>& nums) {
        int n=nums.size();
        long f[n+1];
        f[0]=0;
        for(int i=1;i<n+1;i++){
            f[i]=2*f[i-1]+1;
            f[i]%=mod;
        }

        sort(nums.begin(),nums.end());
        long res=0;
        // 每个元素作为最大最小的元素个数
        for(int i=0;i<n;i++){
            res += (f[i]-f[n-i-1])*nums[i];
            res%=mod;
        }
        return (int)res;
    }
};