第一章 绪论

考点 1：时间复杂度与空间复杂度

时间复杂度

定义：将算法中基本运算的执行次数的数量级作为时间复杂度，记为$O(n)$。

计算原则

• 加法法则：$T(n)=T_1(n)+T_2(n)=O(f(n))+O(g(n))=O(\max (f(n),g(n)))$
• 乘法法则：$T(n)=T_1(n)T_2(n)=O(f(n))O(g(n))=O(f(n)g(n))$

计算方法

• 列方程法：用于递推实现的算法中，设基本运算运行$x$次，找出与问题规模$n$之间的方程关系式，解出$x=f\left(n\right)$，$f\left(n\right)$的最高次数为$k$，则算法的时间复杂度为$O\left(n^k\right)$。
• 递推公式法：用于递归实现的算法中，设$T\left(n\right)$是问题规模为$n$的算法的时间复杂度，$T(n-1)$是问题规模为$n-1$的算法的时间复杂度，建立$T(n)$与$T(n-1)$[或$T(n-2)$等]的递推关系式，根据关系式，解出$T(n)$。

空间复杂度

定义：指算法运行过程中所使用的辅助空间的大小，记为$S(n)$。算法原地工作是指算法所需辅助空间是常量，即$O(1)$。

递归算法特性：

• 一个算法直接或间接调用自身，称为递归调用。
• 必须有一个明确的递归结束条件，称为递归出口。
• 实现递归的关键是建立递归调用工作栈。栈的大小也就是递归深度和递归算法空间复杂度的。

第二章 线性表

考点 2：顺序表

定义：指用一组连续的存储单元，依次存储线性表中的各个元素，从而使得逻辑上相邻的元素在物理位置上也相邻，因此可以随机存取（根据首元素地址和元素序号）表中任何一个元素。

基本操作

• 结构

• 插入

  若表长为$n$,下标从0开始，则在第$i$位置插入元素$e$，则从$a_n$到$a_i$都要向后移动一个位置，共需移动$n-i+1$个元素，平均时间复杂度为$O(n)$。

  //判断1的范围是否有效，否则非法
  //判断当前存储空间是否已满，否则不能插入
  for(int j=L.length;j>=i;--)     //将第1个位置及之后的元素后移
    L.data[j]=L.data[j-1];
  L.data[i-1]=e;                 //在位置i处放入e,数组从0开始存储
  L.length++;                    //线性表长度加1
  

• 删除

  若表长为$n$,下标从$0$开始，当删除第$i个元素时，则从$$a_{i+1}$ 到$a_n$都要向前移动一个位置，共需移动$n-i$个元素，平均时间复杂度为$O(n)$。

  //判断1的范围是否有效
  for(int j=i;j<L.length;j++)     //将第i个位置及之后的元素前移
    L.data[j-1]=L.data[j];
  L.length--;                    //线性表长度减1
  

• 查找

  1. 按序号（下标）查找：顺序表具有随机存取（根据首元地址和序号）的特点，时间复杂度为$O(1)$。
  2. 按值查找：主要运算是比较操作，比较的次数与值在表中的位置和表长有关，平均比较次数为$(n+1)/2$，时间复杂度为$O(n)$。

考点 3：单链表

定义：为了建立元素之间的线性关系，对每个链表结点，除了存放元素自身的信息，还需要存放一个指向其后继的指针。

基本操作

• 查找

  只能从表中第一个结点出发顺序查找，顺着指针$next$域逐个往下搜索，直到找到满足条件的结点为止。时间复杂度为$O(n)$。

• 创建

  1. 头插法：从一个空表开始，然后将新结点插入到当前链表的表头，即头结点之后。

     

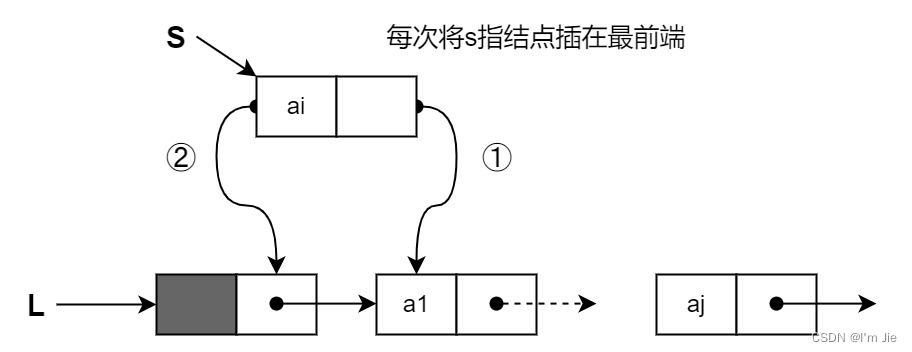
     s->next=L->next;  //①新结点的指针指向原链表的第一个结点
     L->next=s;        //②头结点的指针指向新结点，L为头指针
     

  2. 尾插法：将新结点插入到当前链表的表尾上，为此必须增加一个尾指针 $$r$$，使其始终指向当前链表的尾结点。

     

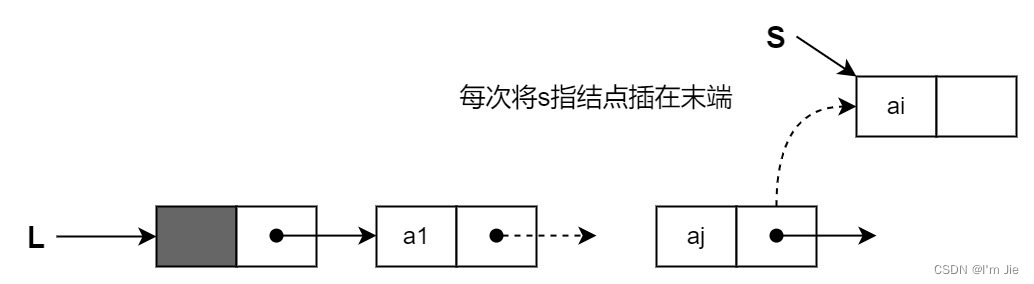
     r->next=s;  //原链表中的尾结点（r所指）的指针指向新结点
     r=s;        //r指向新的表尾结点
     

• 插入

  将值为$x$的新结点插入到单链表的第$i$个位置。先检查插入位置的合法性，然后找到待插入位置的前驱结点，即第$i-1$ 个结点，再在其后插入新结点。

  

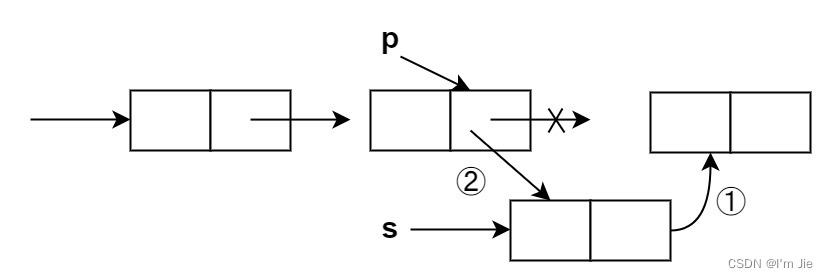
  p=GetElem(L,i-1);   //查找插入位置的前驱结点
  s->next=p->next;    //①s的指针指向p的下一结点
  p->next-s;          //②p的指针指向s
  

• 删除

  将单链表的第$i$个结点删除。先检查删除位置的合法性，然后查找表中第$i-1$ 个结点，即被删结点的前驱结点，再将其删除。

  

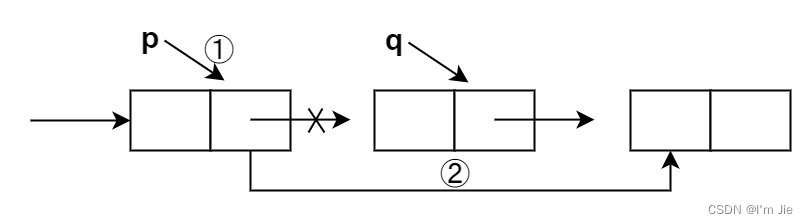
  p=GetElem(L,i-1);    //查找删除位置的前驱结点
  q=p->next;           //令q指向被删除结点
  p->next=q->next;     //将*q结点从链中"断开"
  delete q;            //释放待删结点所占空间
  

• 求表长

  1. 不含头结点：从首结点开始依次顺序访问表中的每个结点，为此需要设置一个计数器变量，每访问一个结点，计数器加$1$，直到访问到$NULL$为止。
  2. 不带头结点的单链表的表长时，对空结点需要单独处理。

  len=0;    //1en表示单链表长度，初值设为0
  LNode *p=L->next;    //令p指向单链表的第一个结点
  while(p) {len++;p=p->next;}    //跳出循环时，len的值即为单链表的长度
  

第三章 栈和队列