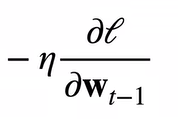---

如有错误，恳请指出。

---

之前有记录过关于图像语义分割的相关评价指标与经典网络，在看PointNet++的语义分割训练脚本的时候，图像的语义分割和点云的语义分割其实本质上是一致的。所以这里想记录一下语义分割的评价指标代码。

1. 定义解析

对于语义分割的准确率评价方法来说，经过资料查询有4种方式：

• 1. pixel accuracy（PA）

定义：分类正确的像素点与所有的像素点数的比例

• 2. mean pixel accuracy（MPA）

定义：计算每一类分类正确的像素点和该类的所有的像素点的比例然后求平均

• 3. mean intersection over union（MIOU）

定义：计算每一类的iou然后求平均（真是集合与预测集合的交并比）

• 4. frequencecy weighted intersection over union （FWIOU）

定义：根据每一类出现的频率对每一类的iou进行加权求和

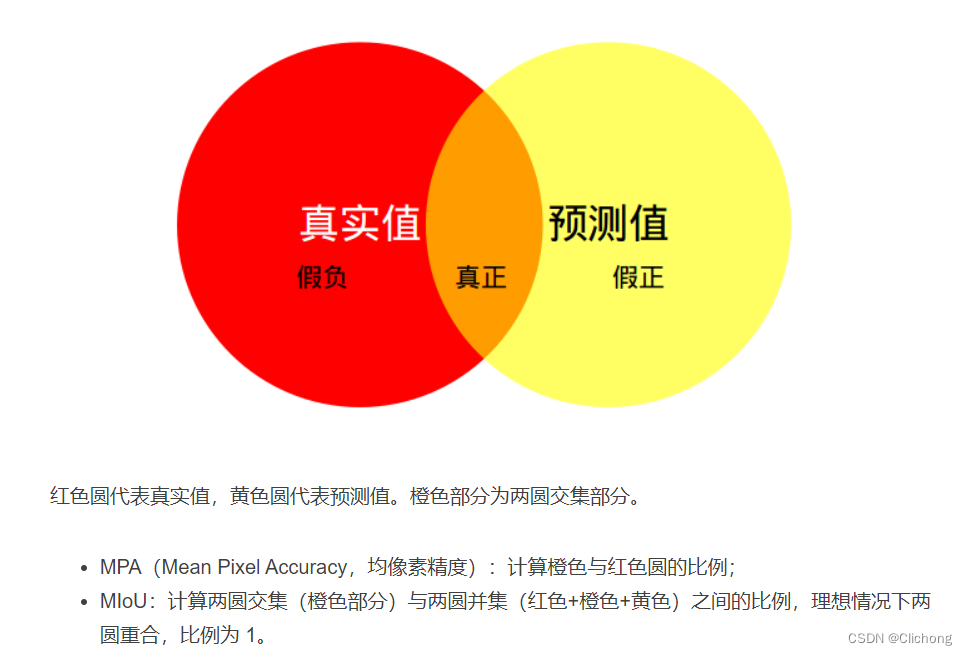
直观理解：

$$MIOU=\frac{1}{k+1}\sum _{k+1}^k\frac{TP}{FN+FP+TP}$$
TP(真正): 预测正确, 预测结果是正类, 真实是正类
FP(假正): 预测错误, 预测结果是正类, 真实是负类
FN(假负): 预测错误, 预测结果是负类, 真实是正类
TN(真负): 预测正确, 预测结果是负类, 真实是负类 #跟类别1无关,所以不包含在并集中

---

2. 代码解析

• 先求出混淆矩阵

• 再根据混淆矩阵进行各指标计算

import numpy as np
import cv2
"""
confusionMetric,真真假假
P\L     P    N
 
P      TP    FP
 
N      FN    TN
 
"""


class Evaluator(object):
    def __init__(self, num_class):
        self.num_class = num_class
        self.confusion_matrix = np.zeros((self.num_class,)*2)
	
	# PA指标计算
    def Pixel_Accuracy(self):
        # acc = (TP + TN) / (TP + TN + FP + TN)
        Acc = np.diag(self.confusion_matrix).sum() / \	# 预测正确总个数
            self.confusion_matrix.sum()					# 全部预测总个数
        return Acc
	
	# MPA指标计算
    def Pixel_Accuracy_Class(self):
        # acc = (TP) / TP + FP
        Acc = np.diag(self.confusion_matrix) / \	# 预测该类别的正确个数
            self.confusion_matrix.sum(axis=1)		# 预测该类别的总个数
        Acc_class = np.nanmean(Acc)
        return Acc_class
	
	# MIOU指标计算
    def Mean_Intersection_over_Union(self):
    	# MIOU = TP / [FN + FP + TP] 
        MIoU = np.diag(self.confusion_matrix) / (		# 预测该类别的正确个数
            np.sum(self.confusion_matrix, axis=1) + 	# 预测该类别的总个数
            np.sum(self.confusion_matrix, axis=0) -		# 该类别真实的总个数
            np.diag(self.confusion_matrix))				# 重叠部分
        MIoU = np.nanmean(MIoU)
        return MIoU
	
	# FWIOU指标计算
    def Frequency_Weighted_Intersection_over_Union(self):
        # FWIOU = [(TP+FN)/(TP+FP+TN+FN)] *[TP / (TP + FP + FN)]
        freq = np.sum(self.confusion_matrix, axis=1) / \	# 每个类别出现的频率
            np.sum(self.confusion_matrix)
        iu = np.diag(self.confusion_matrix) / (				# 每个类别的iou
            np.sum(self.confusion_matrix, axis=1) + 
            np.sum(self.confusion_matrix, axis=0) -
            np.diag(self.confusion_matrix))

        FWIoU = (freq[freq > 0] * iu[freq > 0]).sum()	# 根据频率对iou进行加权
        return FWIoU
	
	# 混淆矩阵生成
	# 参数说明：以图片来说明
	# 		gt_image: target  图片的真实标签            [batch_size, 512, 512]
    # 		per_image: preb   网络生成的图片的预测标签   [batch_size, 512, 512]
    # 如果是点云的话，每个点会预测一个值，所以维度应该如下所示
    # 		gt_point: target  点云的真实标签			   [batch_size, n_points]
    # 		pre_point: pred   网络生成的点云的预测标签   [batch_size, n_points]
    def _generate_matrix(self, gt_image, pre_image):
    	# 对于gt值需要在类别范围内
        mask = (gt_image >= 0) & (gt_image < self.num_class)
        # 核心代码：混淆矩阵是num_class*num_class大小，利用num_class * gt_image是进行预测值的偏移，
      	# 如果预测值与真实值一直，那么相加得到的值会在混淆矩阵的对角线上，表示预测正确(TP),否则会偏移到其他位置则是预测错误
        label = self.num_class * gt_image[mask].astype('int') + pre_image[mask]
        # 利用bincount统计label中每个位置出现的次数
        count = np.bincount(label, minlength=self.num_class**2)
        # reshape构建真正的混淆矩阵，行代表真实类别,列代表预测的类别
        confusion_matrix = count.reshape(self.num_class, self.num_class)
        return confusion_matrix
	
	# 与另一批次的统计结果相加一同计算
    def add_batch(self, gt_image, pre_image):
        assert gt_image.shape == pre_image.shape
        self.confusion_matrix += self._generate_matrix(gt_image, pre_image)
	
	# 重置混淆矩阵
    def reset(self):
        self.confusion_matrix = np.zeros((self.num_class,) * 2)

测试例子，帮助理解（其中a是预测值, b是ground truth）：

>>> b
array([[0, 0, 0, 2],
       [0, 0, 2, 1],
       [1, 1, 1, 0],
       [1, 0, 1, 2]])
>>> a
array([[0, 0, 0, 2],
       [0, 0, 2, 1],
       [1, 1, 1, 2],
       [1, 0, 1, 2]])
>>> label = 3 * b[mask] + a[mask]
>>> count = numpy.bincount(label)
>>> count
array([6, 0, 1, 0, 6, 0, 0, 0, 3])
>>> count = count.reshape(3, 3)
>>> numpy.sum(count, axis=1)
array([7, 6, 3])
>>> numpy.sum(count, axis=0)
array([6, 6, 4])
>>> numpy.sum(count, axis=1) + numpy.sum(count, axis=0)
array([13, 12,  7])
>>> numpy.sum(count, axis=1) + numpy.sum(count, axis=0) - numpy.diag(count)
array([7, 6, 4])

---

参考资料：

1. 语义分割代码阅读—评价指标mIoU的计算

2. 语义分割评价指标，附代码可直接运行

3. Semantic Segmentation | 评价指标与经典网络（FCN，DeepLab系列，UNet，LR-ASPP）

4. MIoU 源码解析