图的生成树与生成森林

news2024/11/23 3:49:50

文章目录

      • 连通图与连通分量
      • 强连通图与强连通分量
      • 图的连通性判断
      • 生成树
        • 深度优先生成树
          • 邻接表
          • 邻接矩阵
        • 广度优先生成树
          • 邻接表
          • 邻接矩阵
        • 生成森林
      • 获取边弧的权值
      • 源代码

连通图与连通分量

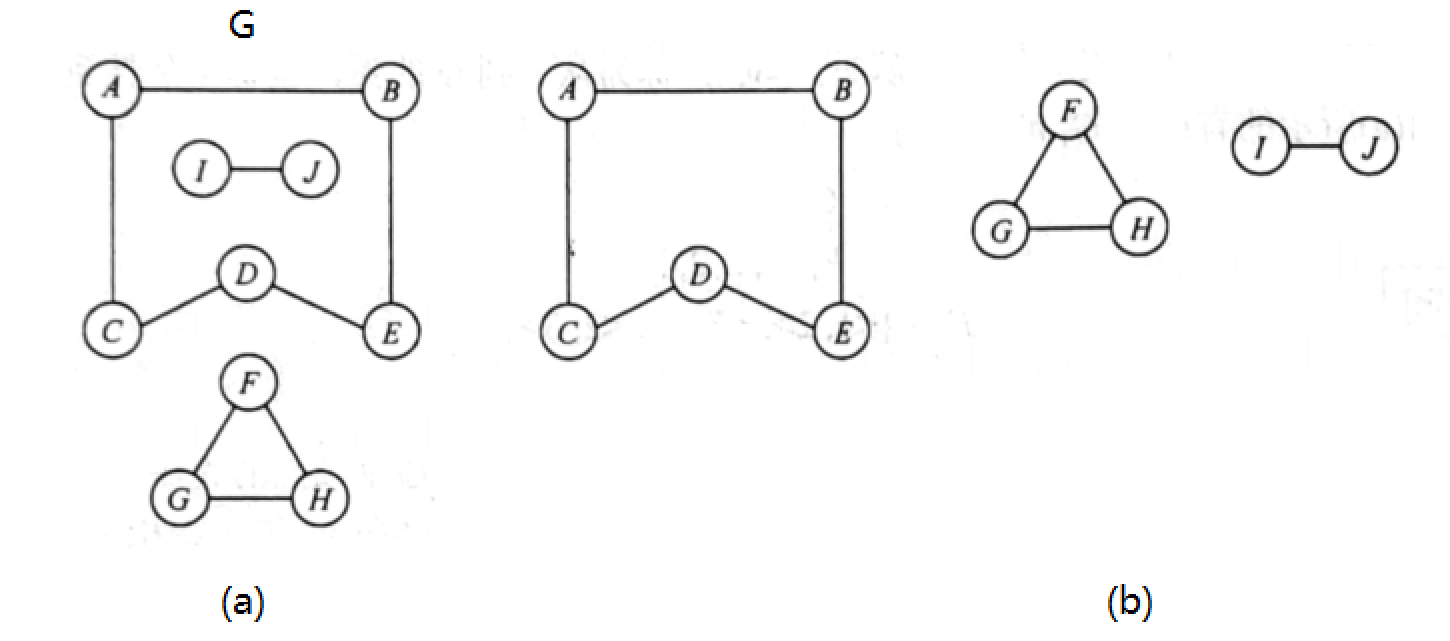
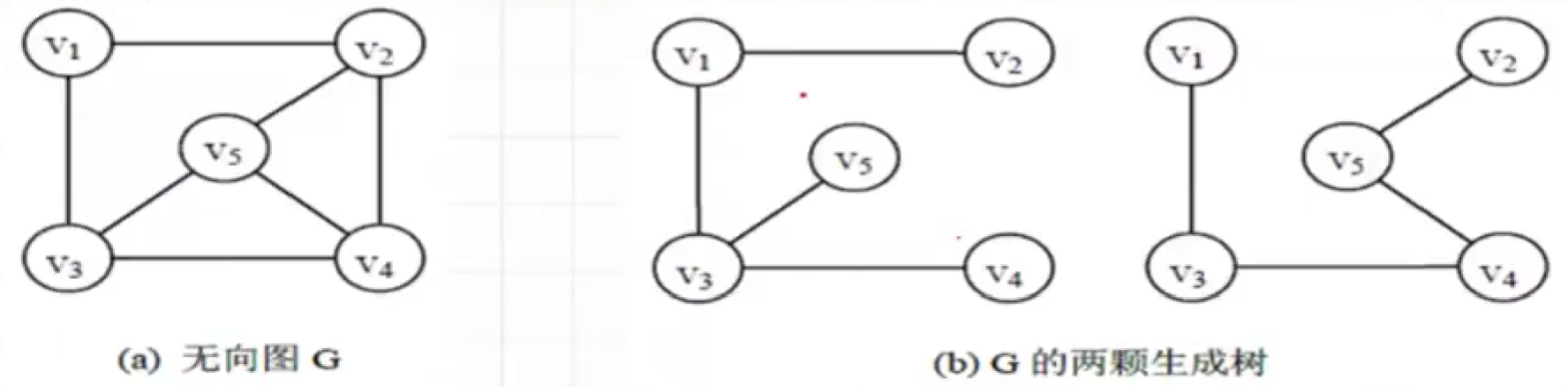
在无向图中, 若从顶点v到顶点w有路径存在, 则称v和w是连通的. 若图G中任意两个顶点都是连通的, 则称图G为连通图, 否则称为非连通图. 无向图中的极大连通子图称为连通分量, 在图(a)中, 图G有3个连通分量如图(b)所示.

假设一个图有n个顶点, 如果边数小于n-1, 那么此图必是非连通图. 如果图是非连通图, 那么最多可以有多少条边?

image-20230106170643111

强连通图与强连通分量

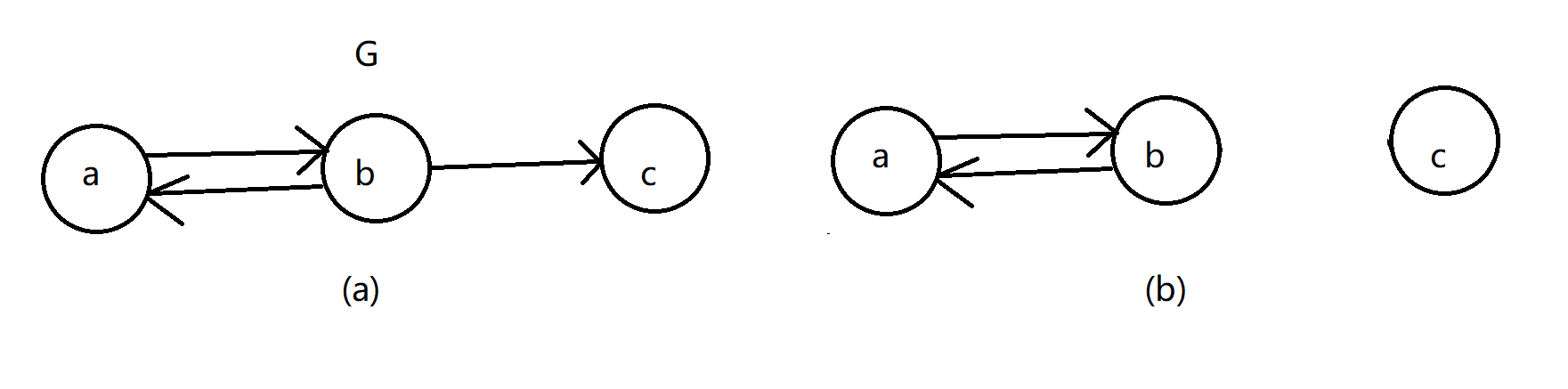
在有向图中, 如果有一对顶点v和w, 从v到w和从w到v之间都有路径, 则称这两个顶点是强连通的. 若图中任何一对顶点都是强连通的, 则称此图为强连通图. 有向图中的极大强连通子图称为有向图的强连通分量, 图G的强连通分量如图(b)所示。

假设一个有向图有n个顶点, 如果是强连通图, 那么最少需要有多少条边.

image-20230106172402815

图的连通性判断

图的遍历算法可以用来判断图的连通性.

对于无向图来说, 若无向图是连通的, 则从任一结点出发, 仅需一次遍历就能够访问图中的所有顶点; 若无向图是非连通的, 则从某一个顶点出发, 一次遍历只能访问到该顶点所在连通分量的所有顶点, 而对于图中其他连通分量的顶点, 则无法通过这次遍历访问.

对于有向图来说, 若从某一顶点到图中的每个顶点都有路径, 则能够访问到图中的所有顶点, 否则不能访问到所有顶点. 因此判断有向图的强连通性, 需要依次从所有顶点出发遍历, 只有从所有顶点出发遍历到其它所有顶点, 该有向图才具有强连通性, 如果从某一个顶点出发遍历, 不能连续遍历到其它顶点, 则该有向图不具有强连通性.

邻接表

		bool _IsConnected(int srci)
		{
			int n = static_cast<int>(_vertexSet.size());

			vector<bool> markbit(n, false);

			queue<int> q;
			q.push(srci);
			markbit[srci] = true;
			// 类似广度优先遍历的思想
			while (!q.empty())
			{
				auto front = q.front();
				q.pop();

				Edge* curr = _table[front];

				while (curr != nullptr)
				{
					if (!markbit[curr->_dsti])
					{
						q.push(curr->_dsti);
						markbit[curr->_dsti] = true;
					}
					curr = curr->_next;
				}
			}
			// 如果还有顶点没有遍历到,说明不是连通图
			for (int i = 0; i < n; i++)
			{
				if (!markbit[i])
				{
					return false;
				}
			}

			return true;
		}

		bool IsConnected()
		{
			if (_vertexSet.empty())
				return true;

			if (Directed) // 有向图的强连通性判断
			{
				int n = static_cast<int>(_vertexSet.size());
				// 需要依次从所有顶点出发遍历
				for (int i = 0; i < n; i++)
				{
					if (!_IsConnected(i))
					{
						return false;
					}
				}

				return true;
			}
			else // 无向图的连通性判断
			{
				return _IsConnected(0);
			}
		}

邻接矩阵

		bool _IsConnected(int srci)
		{
			int n = static_cast<int>(_vertexSet.size());

			vector<bool> markbit(n, false);

			queue<int> q;
			q.push(srci);
			markbit[srci] = true;

			while (!q.empty())
			{
				auto front = q.front();
				q.pop();

				for (int i = 0; i < n; i++)
				{
					if (_matrix[front][i] != W_MAX && !markbit[i])
					{
						q.push(i);
						markbit[i] = true;
					}
				}
			}

			for (int i = 0; i < n; i++)
			{
				if (!markbit[i])
				{
					return false;
				}
			}

			return true;
		}

		bool IsConnected()
		{
			if (_vertexSet.empty())
				return false;

			if (Directed)
			{
				int n = static_cast<int>(_vertexSet.size());

				for (int i = 0; i < n; i++)
				{
					if (!_IsConnected(i))
					{
						return false;
					}
				}

				return true;
			}
			else
			{
				return _IsConnected(0);
			}
		}

生成树

一个连通图的生成树是一个极小连通子图, 它含有图中全部n个顶点, 但只有足以构成一棵树的n-1条边. 在生成树中添加一条边之后, 必然会形成回路/环. 一般来说, 一个连通图的生成树并不是唯一的, 除非原图本身就是一棵树.

image-20230106172904827

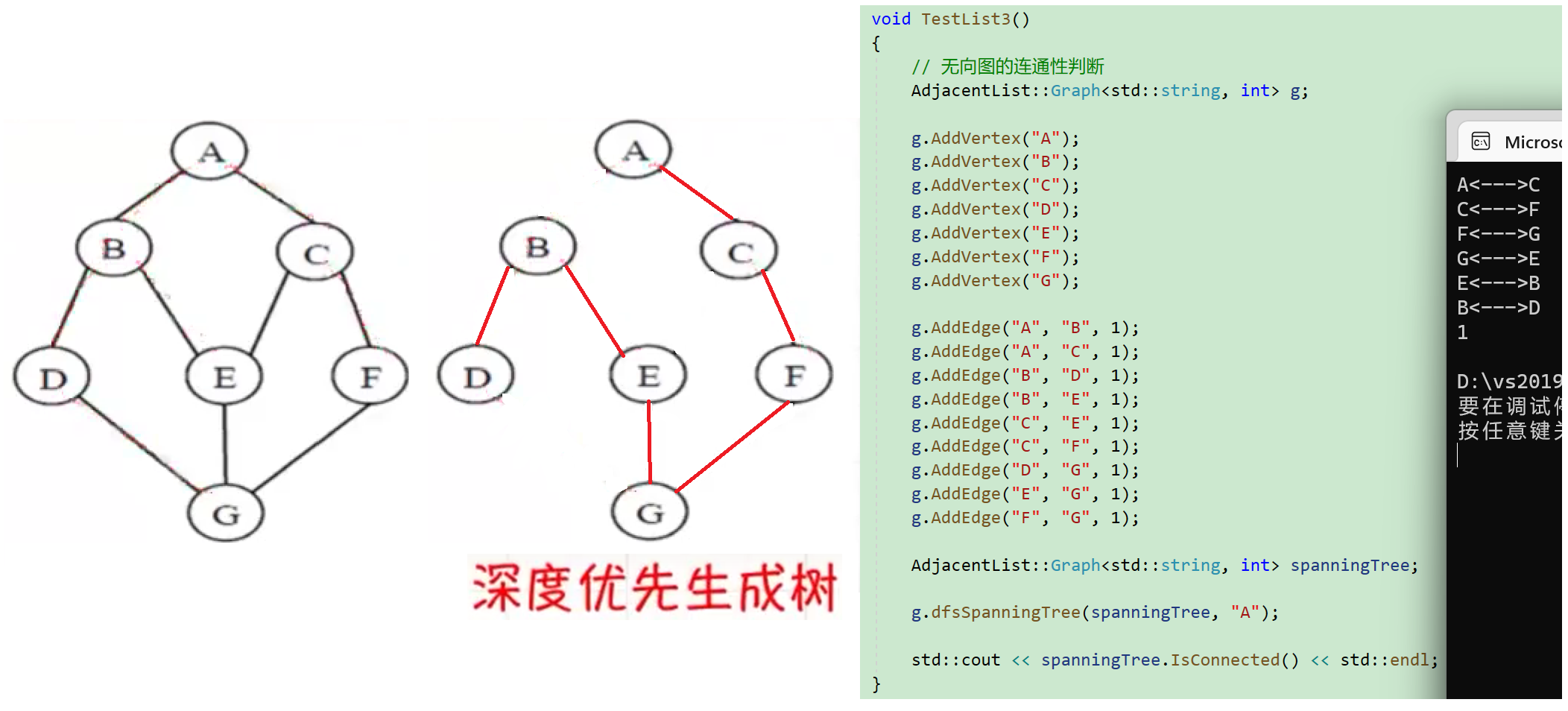
深度优先生成树

采用DFS算法遍历图所得到的生成树称为深度优先生成树.

邻接表

image-20230106190130787

image-20230106185955661

邻接矩阵

image-20230106184009105

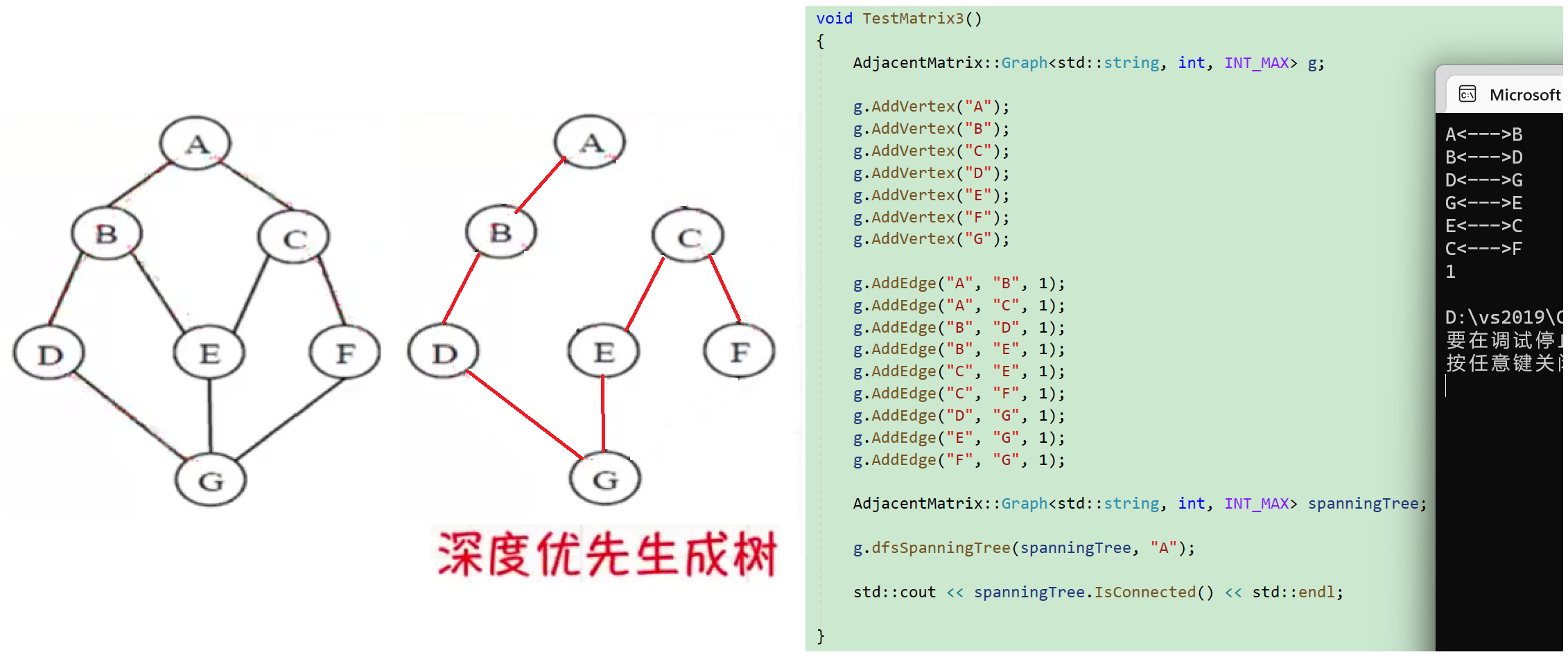
image-20230106185654288

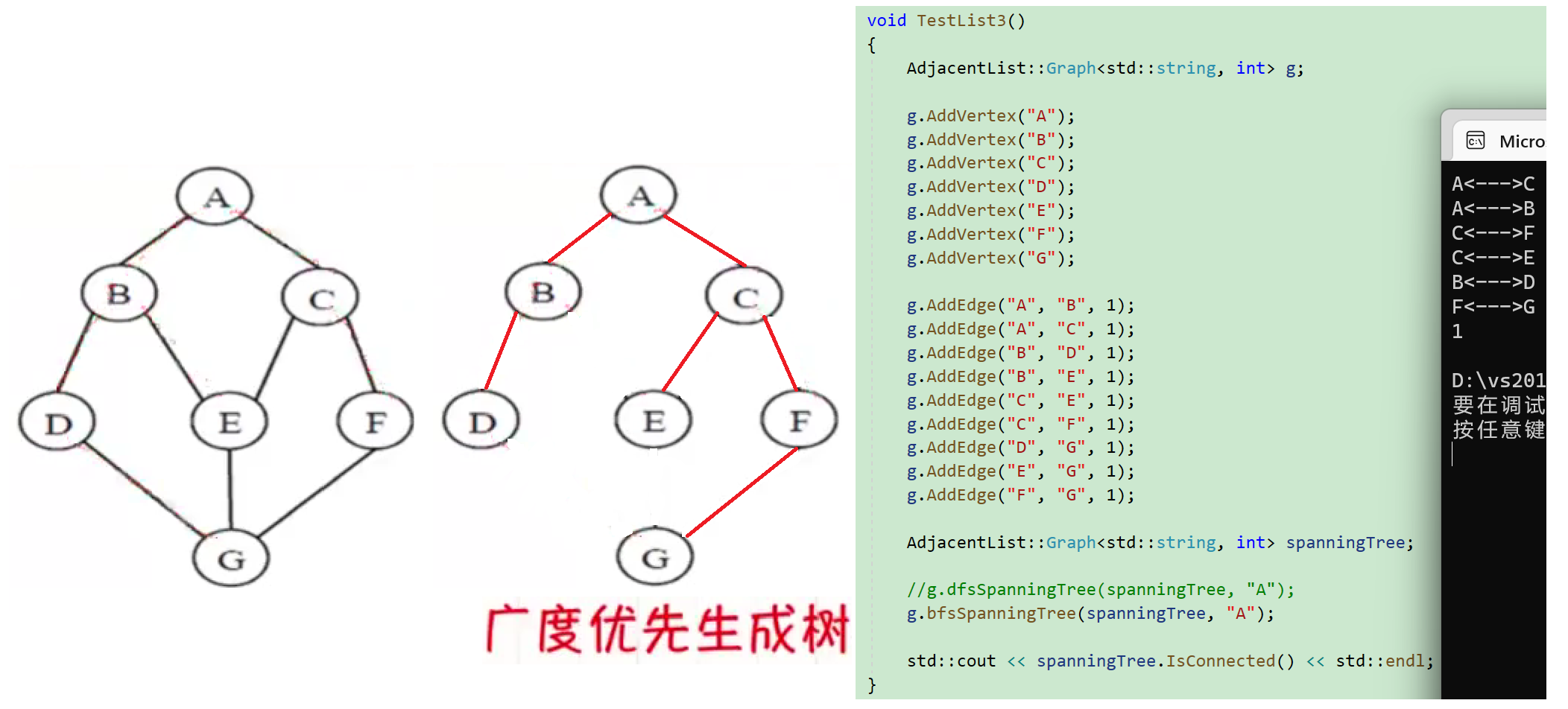
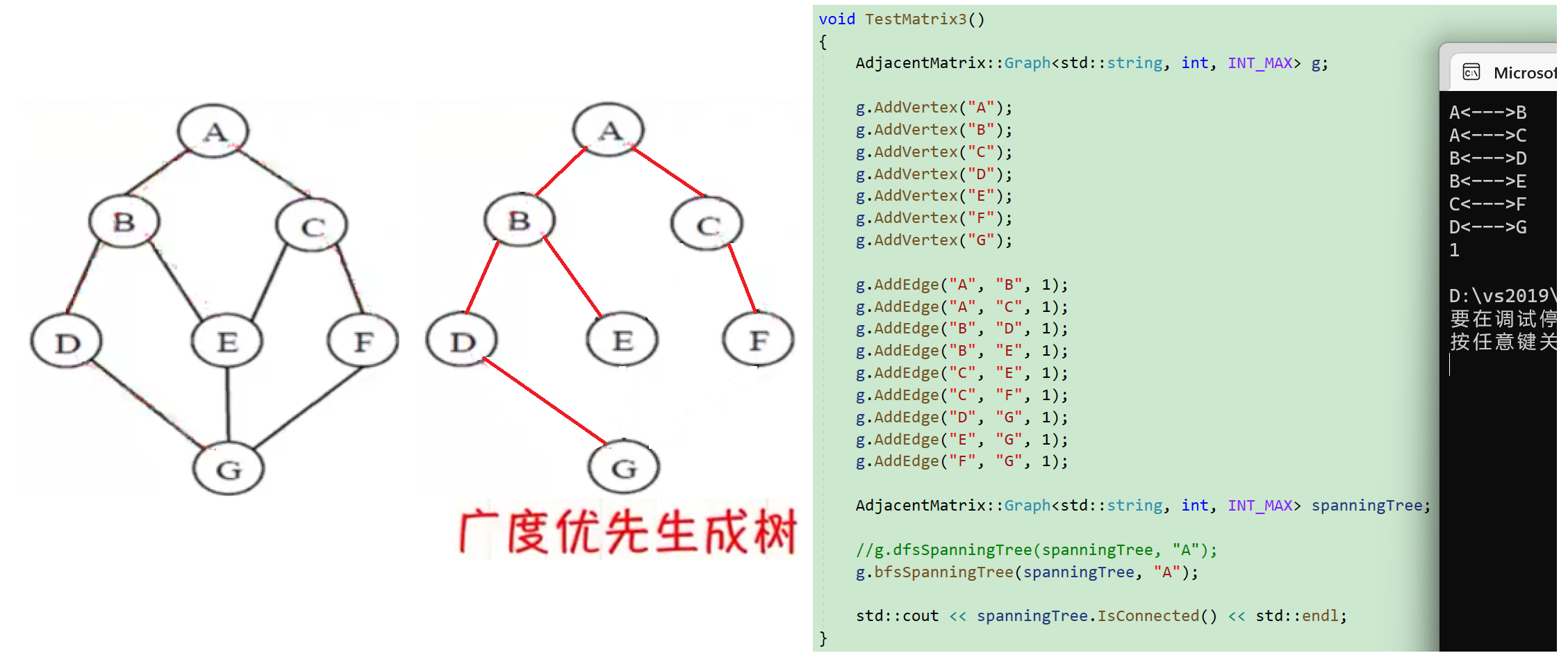
广度优先生成树

采用BFS算法遍历图所得到的生成树称为广度优先生成树.

邻接表

image-20230106203533536

image-20230106203430722

邻接矩阵

image-20230106202923949

image-20230106195948832

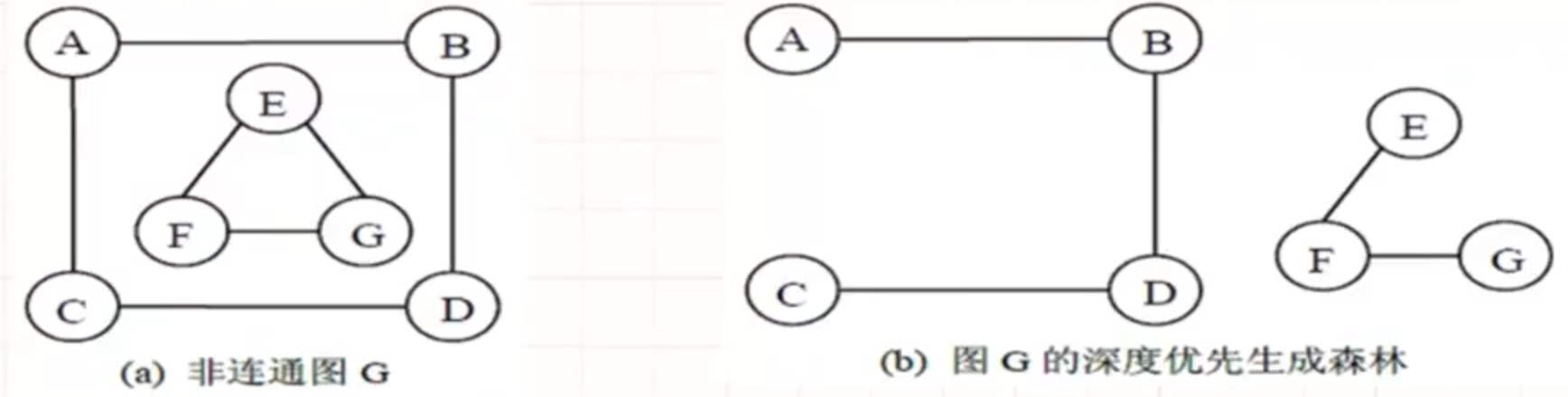
生成森林

若无向图G是非连通图, 从图中某一顶点出发遍历图, 不能访问到该图的所有顶点, 需要依次对图中的每一个连通分量进行深度优先遍历或者广度优先遍历, 即需要从多个顶点出发进行DFS或者BFS.

在遍历过程中, 如果将每次前进途中路过的顶点与边记录下来, 将会得到多棵树, 从而构成森林.

  • 采用DFS算法遍历图所得到的生成森林称为广度优先生成森林.
  • 采用BFS算法遍历图所得到的生成森林称为广度优先生成森林.

image-20230106204243884

获取边弧的权值

邻接表

		// 获取两个相连顶点之间边的权值
		const W& GetEdgeWeight(const V& src, const V& dst)
		{
			int srci = GetVertexIndex(src);
			int dsti = GetVertexIndex(dst);

			if (srci == -1 || dsti == -1)
			{
				return W(); // 可以选择抛异常
			}

			Edge* curr = _table[srci];

			while (curr!=nullptr)
			{
				if (curr->_dsti == dsti)
				{
					return curr->_weight;
				}
				curr=curr->_next;
			}

			return W();
		}

邻接矩阵

		// 获取两个相连顶点之间边的权值
		const W& GetEdgeWeight(const V& src, const V& dst)
		{
			int srci = GetVertexIndex(src);
			int dsti = GetVertexIndex(dst);

			if (srci == -1 || dsti == -1)
			{
				return W(); // 可以选择抛异常
			}
			
			return _matrix[srci][dsti];
		}

源代码

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <cstdio>
#include <vector>
#include <string>
#include <queue>
#include <map>

using namespace std;

namespace AdjacentMatrix
{
	template<typename V, typename W, W W_MAX, bool Directed = false>
	class Graph
	{
	private:
		std::vector<V> _vertexSet;
		std::map<V, int> _vertexIndex;
		std::vector<std::vector<W>> _matrix;
	public:

		typedef Graph<V, W, W_MAX, Directed> Self;

		Graph() = default;

		int GetVertexIndex(const V& v)
		{
			typename std::map<V, int>::iterator pos = _vertexIndex.find(v);
			if (pos != _vertexIndex.end())
			{
				return pos->second;
			}
			else
			{
				return -1;
			}
		}

		// 获取两个相连顶点之间边的权值
		const W& GetEdgeWeight(const V& src, const V& dst)
		{
			int srci = GetVertexIndex(src);
			int dsti = GetVertexIndex(dst);

			if (srci == -1 || dsti == -1)
			{
				return W(); // 可以选择抛异常
			}
			
			return _matrix[srci][dsti];
		}

		bool AddVertex(const V& v)
		{
			// 顶点存在不需要继续增加
			if (GetVertexIndex(v) != -1)
				return false;

			_vertexSet.push_back(v);
			_vertexIndex.insert(std::make_pair(v, _vertexSet.size() - 1));

			// 先在原有的行上一列
			for (int i = 0; i < _matrix.size(); i++)
			{
				_matrix[i].push_back(W_MAX);
			}

			// 增加一行
			_matrix.push_back(std::vector<W>(_vertexSet.size(), W_MAX));

			return true;
		}

		bool AddEdge(const V& src, const V& dst, const W& weight)
		{
			int srci = GetVertexIndex(src);
			int dsti = GetVertexIndex(dst);

			// 顶点不在图中,添加边失败
			if (srci == -1 || dsti == -1)
				return false;

			_matrix[srci][dsti] = weight;

			// 如果为无向图,则需要再添加一条dst->src的边
			if (!Directed)
			{
				_matrix[dsti][srci] = weight;
			}

			return true;
		}

		bool bfsSpanningTree(Self& spanningTree, const V& src)
		{
			int srci = GetVertexIndex(src);

			// 遍历源点不存在,不能进行遍历
			if (srci == -1)
			{
				return false;
			}

			// 只有图为无向图且是连通图才能选出生成树
			if (Directed && !IsConnected())
				return false;
			// 将spanningTree拷贝成与当前图相同顶点的零图
			spanningTree._vertexSet = _vertexSet;
			spanningTree._vertexIndex = _vertexIndex;
			spanningTree._matrix.resize(_vertexSet.size(), vector<W>(_vertexSet.size(), W_MAX));

			vector<bool> visited(_vertexSet.size(), false);
			
			// pair.first是pair.second的上一层顶点下标
			queue<pair<int,int>> q;
			// 将遍历源点下标入队,并标记访问过
			q.push({-1,srci});
			visited[srci] = true;

			while (!q.empty())
			{
				pair<int,int> front = q.front();
				q.pop();

				int first = front.first; // 当前遍历顶点的上一层顶点
				int second = front.second; // 当前遍历顶点

				if (first != -1)
				{
					// 将选出的边添加到spanningTree中
					std::cout << _vertexSet[first] << "<--->" << _vertexSet[second] << std::endl;
					spanningTree.AddEdge(_vertexSet[first], _vertexSet[second], _matrix[first][second]);
				}

				// 将与front.second相连的顶点且没有被访问的顶点入队
				for (int i = 0; i < static_cast<int>(_vertexSet.size()); i++)
				{
					if (_matrix[second][i] != W_MAX && !visited[i])
					{
						// 入队之后标记访问过
						q.push({second,i});
						visited[i] = true; 
					}
				}
			}

			return spanningTree.IsConnected();
		}

		void _dfsSpanningTree(Self& spanningTree, int srci, int& previ, vector<bool>& visited)
		{
			if (previ != -1)
			{
				// 将选出的边添加到spanningTree中
				std::cout << _vertexSet[previ] << "<--->" << _vertexSet[srci] << std::endl;
				spanningTree.AddEdge(_vertexSet[previ], _vertexSet[srci],_matrix[previ][srci]);
			}
			// 标记访问过
			visited[srci] = true;
			// 更新前一个顶点的下标
			previ = srci; 
			// 与DFS遍历的思想相同
			for (int i = 0; i < static_cast<int>(_vertexSet.size()); i++)
			{
				if (_matrix[srci][i] != W_MAX && !visited[i])
				{
					_dfsSpanningTree(spanningTree, i, previ, visited);
				}
			}
			
		}

		bool dfsSpanningTree(Self& spanningTree, const V& src)
		{
			int srci = GetVertexIndex(src);

			// 遍历源点不存在,不能进行遍历
			if (srci == -1)
			{
				return false;
			}

			// 只有图为无向图且是连通图才能选出生成树
			if (Directed && !IsConnected())
				return false;
			// 将spanningTree拷贝成与当前图相同顶点的零图
			spanningTree._vertexSet = _vertexSet;
			spanningTree._vertexIndex = _vertexIndex;
			spanningTree._matrix.resize(_vertexSet.size(), vector<W>(_vertexSet.size(), W_MAX));

			vector<bool> visited(_vertexSet.size(), false);

			int previ = -1; // 遍历访问的前一个顶点下标

			_dfsSpanningTree(spanningTree, srci, previ, visited);

			return spanningTree.IsConnected(); // 如果spanningTree是连通图则说明构建生成树成功
		}

		bool _IsConnected(int srci)
		{
			int n = static_cast<int>(_vertexSet.size());

			vector<bool> markbit(n, false);

			queue<int> q;
			q.push(srci);
			markbit[srci] = true;

			while (!q.empty())
			{
				auto front = q.front();
				q.pop();

				for (int i = 0; i < n; i++)
				{
					if (_matrix[front][i] != W_MAX && !markbit[i])
					{
						q.push(i);
						markbit[i] = true;
					}
				}
			}

			for (int i = 0; i < n; i++)
			{
				if (!markbit[i])
				{
					return false;
				}
			}

			return true;
		}

		bool IsConnected()
		{
			if (_vertexSet.empty())
				return false;

			if (Directed)
			{
				int n = static_cast<int>(_vertexSet.size());

				for (int i = 0; i < n; i++)
				{
					if (!_IsConnected(i))
					{
						return false;
					}
				}

				return true;
			}
			else
			{
				return _IsConnected(0);
			}
		}

	};

	void TestMatrix3()
	{
		AdjacentMatrix::Graph<std::string, int, INT_MAX> g;

		g.AddVertex("A");
		g.AddVertex("B");
		g.AddVertex("C");
		g.AddVertex("D");
		g.AddVertex("E");
		g.AddVertex("F");
		g.AddVertex("G");

		g.AddEdge("A", "B", 1);
		g.AddEdge("A", "C", 1);
		g.AddEdge("B", "D", 1);
		g.AddEdge("B", "E", 1);
		g.AddEdge("C", "E", 1);
		g.AddEdge("C", "F", 1);
		g.AddEdge("D", "G", 1);
		g.AddEdge("E", "G", 1);
		g.AddEdge("F", "G", 1);

		AdjacentMatrix::Graph<std::string, int, INT_MAX> spanningTree;

		//g.dfsSpanningTree(spanningTree, "A");
		g.bfsSpanningTree(spanningTree, "A");

		std::cout << spanningTree.IsConnected() << std::endl;
	}

}

namespace AdjacentList
{
	template<typename W>
	struct Edge
	{
		int _dsti;
		W _weight;

		struct Edge<W>* _next;

		Edge(int dsti, const W& weight)
			:_dsti(dsti)
			, _weight(weight)
			, _next(nullptr)
		{}
	};

	template<typename V, typename W, bool Directed = false>
	class Graph
	{
		using Edge = Edge<W>;
	private:
		std::vector<V> _vertexSet; // 顶点的集合
		std::map<V, int> _vertexIndex; // 顶点映射下标
		std::vector<Edge*> _table; // 出度边表
	public:

		typedef Graph<V, W,Directed> Self;

		Graph() = default;

		int GetVertexIndex(const V& v)
		{
			typename std::map<V, int>::iterator pos = _vertexIndex.find(v);
			if (pos != _vertexIndex.end())
			{
				return pos->second;
			}
			else
			{
				return -1;
			}
		}

		bool AddVertex(const V& v)
		{
			if (GetVertexIndex(v) != -1)
				return false;

			_vertexSet.push_back(v);

			_vertexIndex.insert(std::make_pair(v, _vertexSet.size() - 1));

			_table.push_back(nullptr);

			return true;
		}

		bool AddEdge(const V& src, const V& dst, const W& weight)
		{
			int srci = GetVertexIndex(src);
			int dsti = GetVertexIndex(dst);

			// 顶点不在图中,添加边失败
			if (srci == -1 || dsti == -1)
				return false;

			Edge* edge = new Edge(dsti, weight);

			// 头插
			edge->_next = _table[srci];
			_table[srci] = edge;

			// 无向图
			if (!Directed)
			{
				edge = new Edge(srci, weight);

				edge->_next = _table[dsti];
				_table[dsti] = edge;
			}

			return true;
		}

		bool _IsConnected(int srci)
		{
			int n = static_cast<int>(_vertexSet.size());

			vector<bool> markbit(n, false);

			queue<int> q;
			q.push(srci);
			markbit[srci] = true;
			// 类似广度优先遍历的思想
			while (!q.empty())
			{
				auto front = q.front();
				q.pop();

				Edge* curr = _table[front];

				while (curr != nullptr)
				{
					if (!markbit[curr->_dsti])
					{
						q.push(curr->_dsti);
						markbit[curr->_dsti] = true;
					}
					curr = curr->_next;
				}
			}
			// 如果还有顶点没有遍历到,说明不是连通图
			for (int i = 0; i < n; i++)
			{
				if (!markbit[i])
				{
					return false;
				}
			}

			return true;
		}

		bool IsConnected()
		{
			if (_vertexSet.empty())
				return true;

			if (Directed) // 有向图的强连通性判断
			{
				int n = static_cast<int>(_vertexSet.size());
				// 需要依次从所有顶点出发遍历
				for (int i = 0; i < n; i++)
				{
					if (!_IsConnected(i))
					{
						return false;
					}
				}

				return true;
			}
			else // 无向图的连通性判断
			{
				return _IsConnected(0);
			}
		}

		// 获取两个相连顶点之间边的权值
		const W& GetEdgeWeight(const V& src, const V& dst)
		{
			int srci = GetVertexIndex(src);
			int dsti = GetVertexIndex(dst);

			if (srci == -1 || dsti == -1)
			{
				return W(); // 可以选择抛异常
			}

			Edge* curr = _table[srci];

			while (curr!=nullptr)
			{
				if (curr->_dsti == dsti)
				{
					return curr->_weight;
				}
				curr=curr->_next;
			}

			return W();
		}

		bool bfsSpanningTree(Self& spanningTree, const V& src)
		{
			int srci = GetVertexIndex(src);

			// 遍历源点不存在,不能进行遍历
			if (srci == -1)
			{
				return false;
			}

			// 只有图为无向图且是连通图才能选出生成树
			if (Directed && !IsConnected())
				return false;
			// 将spanningTree拷贝成与当前图相同顶点的零图
			spanningTree._vertexSet = _vertexSet;
			spanningTree._vertexIndex = _vertexIndex;
			spanningTree._table.resize(_vertexSet.size(), nullptr);

			vector<bool> visited(_vertexSet.size(), false);

			// pair.first是pair.second的上一层顶点下标
			queue<pair<int, int>> q;
			// 将遍历源点下标入队,并标记访问过
			q.push({ -1,srci });
			visited[srci] = true;

			while (!q.empty())
			{
				pair<int, int> front = q.front();
				q.pop();

				int first = front.first; // 当前遍历顶点的上一层顶点
				int second = front.second; // 当前遍历顶点

				if (first != -1)
				{
					// 将选出的边添加到spanningTree中
					std::cout << _vertexSet[first] << "<--->" << _vertexSet[second] << std::endl;
					spanningTree.AddEdge(_vertexSet[first], _vertexSet[second], 
						GetEdgeWeight(_vertexSet[first], _vertexSet[second]));
				}

				Edge* curr = _table[second];

				// 将与front.second相连的顶点且没有被访问的顶点入队
				while (curr != nullptr)
				{
					if (!visited[curr->_dsti])
					{
						q.push({ second,curr->_dsti });
						visited[curr->_dsti] = true;
					}

					curr = curr->_next;
				}
			}

			return spanningTree.IsConnected();
		}

		void _dfsSpanningTree(Self& spanningTree, int srci, int& previ, vector<bool>& visited)
		{
			if (previ != -1)
			{
				// 将选出的边添加到spanningTree中
				std::cout << _vertexSet[previ] << "<--->" << _vertexSet[srci] << std::endl;
				spanningTree.AddEdge(_vertexSet[previ], _vertexSet[srci], GetEdgeWeight(_vertexSet[previ], _vertexSet[srci]));
			}
			// 标记访问过
			visited[srci] = true;
			// 更新前一个顶点的下标
			previ = srci;

			Edge* curr = _table[srci];

			while (curr != nullptr)
			{
				if (!visited[curr->_dsti])
				{
					_dfsSpanningTree(spanningTree, curr->_dsti, previ, visited);
				}
				curr = curr->_next;
			}
		}
		// spanningTree为输出型参数,src为遍历源点
		bool dfsSpanningTree(Self& spanningTree, const V& src)
		{
			int srci = GetVertexIndex(src);

			// 遍历源点不存在,不能进行遍历
			if (srci == -1)
			{
				return false;
			}

			// 只有图为无向图且是连通图才能选出生成树
			if (Directed && !IsConnected())
				return false;
			// 将spanningTree拷贝成与当前图相同顶点的零图
			spanningTree._vertexSet = _vertexSet;
			spanningTree._vertexIndex = _vertexIndex;
			spanningTree._table.resize(_vertexSet.size(), nullptr);

			vector<bool> visited(_vertexSet.size(), false);

			int previ = -1; // 遍历访问的前一个顶点下标

			_dfsSpanningTree(spanningTree, srci, previ, visited);

			return spanningTree.IsConnected(); // 如果spanningTree是连通图则说明构建生成树成功
		}

	};

	void TestList3()
	{ 
		AdjacentList::Graph<std::string, int> g;

		g.AddVertex("A");
		g.AddVertex("B");
		g.AddVertex("C");
		g.AddVertex("D");
		g.AddVertex("E");
		g.AddVertex("F");
		g.AddVertex("G");

		g.AddEdge("A", "B", 1);
		g.AddEdge("A", "C", 1);
		g.AddEdge("B", "D", 1);
		g.AddEdge("B", "E", 1);
		g.AddEdge("C", "E", 1);
		g.AddEdge("C", "F", 1);
		g.AddEdge("D", "G", 1);
		g.AddEdge("E", "G", 1);
		g.AddEdge("F", "G", 1);

		AdjacentList::Graph<std::string, int> spanningTree;

		//g.dfsSpanningTree(spanningTree, "A");
		g.bfsSpanningTree(spanningTree, "A");

		std::cout << spanningTree.IsConnected() << std::endl;
	}
}


int main(int, char**, char**)
{

	AdjacentList::TestList3();
	//AdjacentMatrix::TestMatrix3();
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/144625.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

动态规划--矩阵链相乘问题

动态规划--矩阵链相乘问题

明确原始问题A[1:n]&#xff1a;计算矩阵链 所需的最小乘法次数。 &#xff08;1&#xff09;是否满足最优子结构&#xff0c;问题的解是否包含子问题的优化解&#xff1f; 若计算A[1:n]的优化顺序在k处断开矩阵链&#xff0c;即A[1:n]A[1:k]A[k1:n],则在A[1:n]的优化顺序中&a…
阅读更多...
ReFactor GNN：从消息传递角度重新审视FMs

ReFactor GNN：从消息传递角度重新审视FMs

分享嘉宾 | 陈艺虹 文稿整理 | William Knowledge Graph Completion(KGC) 知识图谱一般会有多个节点&#xff0c;包括性别、国家等各种各样的节点(也可理解为实体)&#xff0c;节点之间会有不同的关系&#xff0c;可以通过其他的一些节点预测出当前节点的其他信息。恢复这些信…
阅读更多...
2023/1/6 Vue学习笔记-1

2023/1/6 Vue学习笔记-1

尝试 Vue.js 最简单的方法是使用 Hello World 例子。你可以在浏览器新标签页中打开它&#xff0c;跟着例子学习一些基础用法。或者你也可以创建一个 .html 文件&#xff0c;然后通过如下方式引入 Vue&#xff1a; <!-- 开发环境版本&#xff0c;包含了有帮助的命令行警告 -…
阅读更多...
设计模式——建造者模式

设计模式——建造者模式

文章目录模式理解基本概念使用示例建造者模式延展模式理解 建造者模式&#xff08;Builder Pattern&#xff09;&#xff1a;建造者模式是一种对象创建型模式。将一个复杂对象的构建与它的表示分离&#xff0c;使得同样的构建过程可以创建不同的表示。这句话理解起来太抽象了&…
阅读更多...
B. Dima and a Bad XOR(构造 + 异或性质)

B. Dima and a Bad XOR(构造 + 异或性质)

Problem - 1151B - Codeforces 来自Kremland的学生Dima有一个大小为nm的非负整数矩阵a。 他希望从矩阵的每一行中选择一个整数&#xff0c;以便所选整数的按位互斥或严格大于0。帮助他! 形式上&#xff0c;他想选择一个整数序列c1,c2&#xff0c;…&#xff0c;cn(1≤cj≤m)&am…
阅读更多...
Integer包装类详解(java)

Integer包装类详解(java)

文章目录&#x1f4d6;前言&#xff1a;&#x1f380;包装类概念&#xff1a;&#x1f380;包装类分类&#xff1a;&#x1f380;包装类integer介绍&#xff1a;&#x1f387;自动装箱和自动拆箱问题【⚠注意面试常考点】&#x1f387;Integer常用方法&#xff1a;&#x1f4d6…
阅读更多...
2023真无线蓝牙耳机推荐：高性价比真无线蓝牙耳机各价位蓝牙耳机推荐！

2023真无线蓝牙耳机推荐：高性价比真无线蓝牙耳机各价位蓝牙耳机推荐！

2023年了&#xff0c;蓝牙耳机赛道依然很卷&#xff01;性价比是反映物品可买程度的一种量化的计量方式。现如今&#xff0c;蓝牙耳机市场上主打高性价比的不在少数&#xff0c;而高性价比的东西往往更能精准抓住用户“痛点”&#xff0c;从而受到了不少用户的欢迎。 既然高性…
阅读更多...
面试20分钟就完事了，问的实在是太......

面试20分钟就完事了，问的实在是太......

干了两年外包&#xff0c;本来想出来正儿八经找个互联网公司上班&#xff0c;没想到算法死在另一家厂子。 自从加入这家外包公司&#xff0c;每天都在加班&#xff0c;钱倒是给的不少&#xff0c;所以也就忍了。没想到11月一纸通知&#xff0c;所有人不许加班&#xff0c;薪资…
阅读更多...
Spring Boot整合Junit

Spring Boot整合Junit

系列文章目录 Spring Boot[概述、功能、快速入门]_心态还需努力呀的博客-CSDN博客 Spring Boot读取配置文件内容的三种方式_心态还需努力呀的博客-CSDN博客 该系列文章持续更新中~ 目录 系列文章目录 前言 一、搭建SpringBoot工程 二、引入starter-test起步依赖 三、编…
阅读更多...
2022年全国研究生数学建模竞赛华为杯F题COVID-19疫情期间生活物资的科学管理问题求解全过程文档及程序

2022年全国研究生数学建模竞赛华为杯F题COVID-19疫情期间生活物资的科学管理问题求解全过程文档及程序

2022年全国研究生数学建模竞赛华为杯 F题 COVID-19疫情期间生活物资的科学管理问题 原题再现&#xff1a; 一、背景介绍   进入2022年以来全国范围内陆续出现了多次较大规模疫情爆发事件[1-2]。在大规模疫情爆发期间由于我国采用封闭式管理方式来实现疫情的快速清零&#x…
阅读更多...
Vue组件之间的通信（组件之间的数据传递）

Vue组件之间的通信（组件之间的数据传递）

一、Vue组件之间的关系 父子关系&#xff1a;A组件和B组件、B组件和C组件、B组件和D组件​ 兄弟关系&#xff1a;C组件和D组件​ 隔代关系&#xff1a;A组件和C组件、A组件和D组件 二、父组件向子组件传递数据 通过props方式向子组件传递数据&#xff08;在子组件中添加props属…
阅读更多...
为什么选型低代码平台时，需要注重私有化部署能力？

为什么选型低代码平台时，需要注重私有化部署能力？

编者按&#xff1a;低代码平台&#xff0c;目前分为私有化部署和公有化部署&#xff0c;企业为什么倾向于选择私有化部署的低代码平台&#xff1f;本文从私有化部署的概念出发&#xff0c;分析了私有化部署的优势&#xff0c;并进一步介绍了支持私有化部署的老牌低代码平台。关…
阅读更多...
工控安全-使用Metasploit攻击Modbus设备

工控安全-使用Metasploit攻击Modbus设备

文章目录实验内容环境介绍实验开始开启Modbus从站主机和从站服务利用Metasploit工具扫描Modbus从站中的ID访问从站2的寄存器数据修改从站4线圈值可选择的action实验内容 利用Metasploit工具针对Modbus协议进行攻击&#xff0c;读取Modbus从站寄存器数值以及修改Modbus从站寄存…
阅读更多...
应届生学习Java八个月，offer年薪28W，这一年我经历了什么？

应届生学习Java八个月，offer年薪28W，这一年我经历了什么？

自我介绍 首页和大家介绍一下我&#xff0c;我叫 阿杆&#xff08;笔名及游戏名&#x1f923;&#xff09;&#xff0c;19级本科在读&#xff0c;双非院校&#xff0c;主修软件工程&#xff0c;学习方向是后端开发&#xff0c;主要语言Java、Python&#xff0c;今年秋招拿到了…
阅读更多...
三、Gtk4-Widgets（1）

三、Gtk4-Widgets（1）

1 GtkLavel&#xff0c;GtkButton and GtkBox 1.1 GtkLabel 在前一节中&#xff0c;我们创建了一个窗口并将其显示在屏幕上。现在我们进入下一个主题&#xff0c;在这个窗口中添加部件。最简单的部件是GtkLabel。它是一个包含文本的部件。 1 #include <gtk/gtk.h>2 3 s…
阅读更多...
spark sql 执行流程

spark sql 执行流程

最近学习了spark sql执行流程&#xff0c;从网上搜到了大都是sql解析、analyzer、optimizer阶段、sparkplan阶段&#xff0c;但是我比较好奇的是&#xff0c;这几个阶段是怎么串起来的&#xff0c;于是花了好几天着重从源码层面看看了看具体实现&#xff0c;写了几点自己认为应…
阅读更多...
聊聊Mybatis的缓存

聊聊Mybatis的缓存

Mybatis缓存是内存中的数据&#xff0c;主要是对数据库查询结果的保存&#xff0c;使用缓存的好处是避免频繁与数据库进行交互&#xff0c;提升查询的响应速度。 数据库缓存扩展 聊到Mybatis缓存。我们可以扩展聊一下MySQL缓存。MySQL缓存其实与Mybatis类似&#xff0c;在查询…
阅读更多...
物联网架构实例—Ubuntu 安装MongoDB及完全卸载

物联网架构实例—Ubuntu 安装MongoDB及完全卸载

1.安装1.1.导入公钥wget -qO - https://www.mongodb.org/static/pgp/server-4.4.asc | sudo apt-key add -如果收到指示gnupg未安装的错误&#xff0c;则可以先执行&#xff1a;sudo apt-get install gnupg然后再执行一次导入公钥命令&#xff1a;wget -qO - https://www.mongo…
阅读更多...
React（coderwhy）- 08(Hooks)

React（coderwhy）- 08(Hooks)

认识和体验Hooks 为什么需要Hook? ◼ Hook 是 React 16.8 的新增特性&#xff0c;它可以让我们在不编写class的情况下使用state以及其他的React特性&#xff08;比如生命周期&#xff09;。 ◼ 我们先来思考一下class组件相对于函数式组件有什么优势&#xff1f;比较常见的是下…
阅读更多...
Exynos_4412——IIC总线概述

Exynos_4412——IIC总线概述

目录 一、IIC总线概述 1.1IIC总线简介 1.2IIC总线通信过程 1.3IIC总线寻址方式 二、IIC总线信号实现 2.1起始信号与停止信号 2.2字节传送与应答 2.3同步信号 三、典型IIC时序 四、小作业 一、IIC总线概述 1.1IIC总线简介 IIC总线IIC总线是Philips公司在八十年代初推…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023