论文阅读
- 1. 本周计划
- 2. 完成情况
- 2.1 论文摘要
- 2.2 网络结构
- 2.3 损失函数
- 2.4 优化器
- 2.5 代码
- 2.5.1 代码结果
- 2.5.2 代码大致流程
- 4. 总结及收获
- 4. 下周计划
1. 本周计划
阅读论文《Data-Driven Seismic Waveform Inversion: A Study on the Robustness and Generalization》并实现论文代码,学习代码套路
2. 完成情况
2.1 论文摘要
Full-waveform inversion is an important and widely used method to reconstruct subsurface velocity images. Waveform inversion is a typical nonlinear and ill-posed inverse problem. Existing physics-driven computational methods for solving waveform inversion suffer from the cycle-skipping and local-minima issues, and do not mention that solving waveform inversion is computationally expensive. In recent years, data-driven methods become a promising way to solve the waveform-inversion problem. However, most deep-learning frameworks suffer from the generalization and overfitting issue. In this article, we developed a real-time data-driven technique and we call it VelocityGAN, to reconstruct accurately the subsurface velocities. Our VelocityGAN is built on a generative adversarial network (GAN) and trained end to end to learn a mapping function from the raw seismic waveform data to the velocity image. Different from other encoder–decoder-based data-driven seismic waveform-inversion approaches, our VelocityGAN learns regularization from data and further imposes the regularization to the generator so that inversion accuracy is improved. We further develop a transfer-learning strategy based on VelocityGAN to alleviate the generalization issue. A series of experiments is conducted on the synthetic seismic reflection data to evaluate the effectiveness, efficiency, and generalization of VelocityGAN. We not only compare it with the existing physics-driven approaches and datadriven frameworks but also conduct several transfer-learning experiments. The experimental results show that VelocityGAN achieves the state-of-the-art performance among the baselines and can improve the generalization results to some extent.
在摘要部分,论文作者提出了解决FWI的物理驱动计算方法主要面临的问题
- 周期跳跃问题
- 局部最小值问题
- 计算成本很高
论文中提出了一种实时的数据驱动技术VelocityGAN,利用生成对抗网络(GAN)从原始地震波形数据到速度图像的映射函数,论文主要的创新点:
- 实时数据驱动技术
- 从数据中学习正则化,并将正则化施加给生成器,
- 基于VelocityGAN的迁移学习策略来缓解泛化问题
2.2 网络结构
VelocityGan 由两部分组成:生成器和判别器;其中生成器是一种编码器-解码器结构,将原始地震数据映射到速度图像;鉴别器是一个卷积神经网络(CNN),对真实或假的速度图像进行分类.如下是网络结构图:
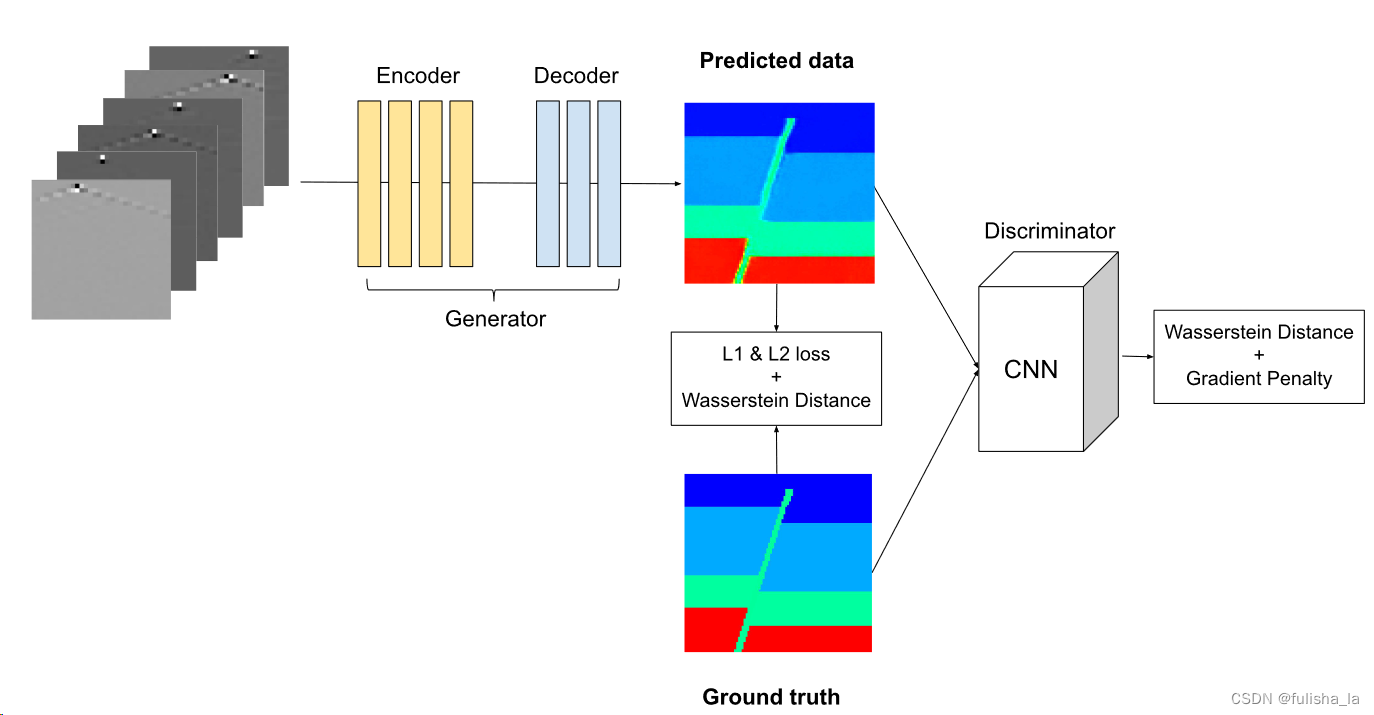
-
生成器Generator
在论文中生成器的结构如下表TABLE I所示,这个结构其实和InversionNet的网络结构很相似


但是在最新的代码中,输入的图像为 5 ∗ 1000 ∗ 70 5*1000*70 5∗1000∗70,输出为 1 ∗ 70 ∗ 70 1*70*70 1∗70∗70 为啥要改变尺寸大小? 为啥要改变尺寸大小? 为啥要改变尺寸大小? -
判别器Generator
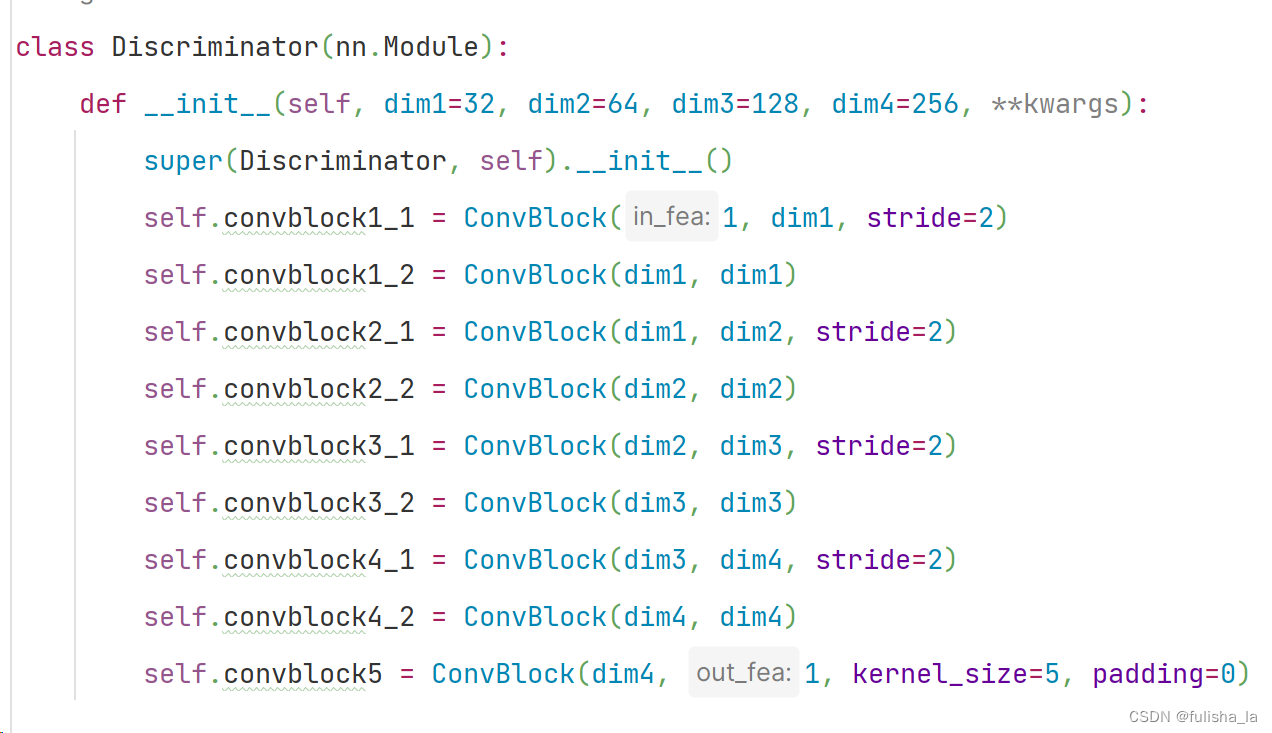
Discriminator: Similar to Radford et al. [35], we adapt our discriminator from a CNN architecture. In particular, it consists of five convolution blocks, a global average pooling layer, and fully connected layers. Each convolutional block involves a combination of Convolutional, BatchNormalization, LeakyReLU, and MaxPooling layers. We apply the “PatchGAN” classifier [18] in the discriminator to capture local style statistics. We set the patch size as 4 and calculate the mean loss value of all patches in an image
在论文中,判别器主要由五个卷积块、一个全局平均池化层和全连接层组成,还应用了PatchGAN分类器,而在现在的代码中发现已经取消了PathGan.也没由全连接层和平均池化层了。 这貌似就和论文中的出入较大。(patchGan: 主要用在判别器上,比如的GAN网络输入为一张图像输出一个单一的判别结果true or false, 而patchGan使用了局部感受野,转为对图像局部区域进行判别,若输入一张图像,输出就是一个N*N的矩阵。)
2.3 损失函数
- 生成器损失函数
def criterion_g(pred, gt, model_d=None): # 预测值和真实值?
loss_g1v = l1loss(pred, gt)
loss_g2v = l2loss(pred, gt)
loss = args.lambda_g1v * loss_g1v + args.lambda_g2v * loss_g2v
if model_d is not None:
loss_adv = -torch.mean(model_d(pred))
loss += args.lambda_adv * loss_adv
return loss, loss_g1v, loss_g2v
生成器损失函数公式:
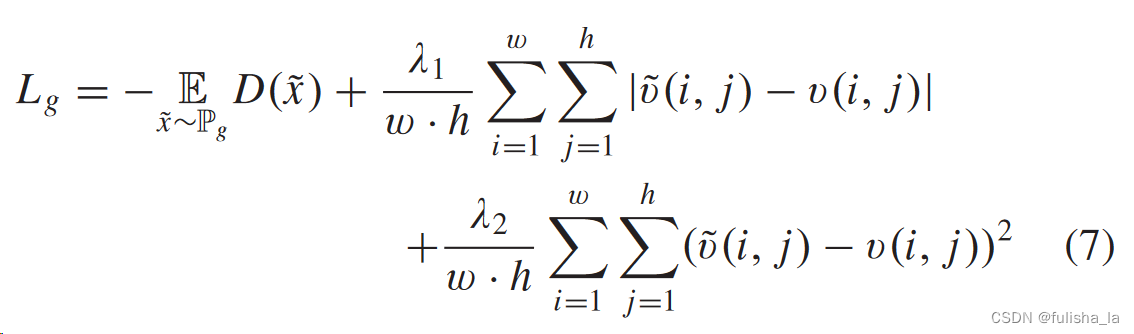
-
L1loss函数是MAE(MAE loss performs better on revealing the geological interfaces); L2loss函数是MSE(MSE loss is good at capturing the geological faults)
-
loss 总损失值是根据权重系数计算得到。(平衡损失项的重要性)
-
loss_adv:在生成器损失函数中,若提供了判别器,则需要计算对抗损失项loss_adv,首先需要将预测值输入到判别器模型中得到判别结果。再将判别结果取负均值。 这样的目的是最大化生成器生成图像被判别器判别为真的概率。即负均值越接近0,则说明生成的图像被判别为真实图像的概率越高,从而生成器的性能越好。并最后将这个损失函数加入到总损失函数 中。
最后返回生成器相关的损失函数 -
判别器损失函数
class Wasserstein_GP(nn.Module):
def __init__(self, device, lambda_gp):
super(Wasserstein_GP, self).__init__()
self.device = device
self.lambda_gp = lambda_gp
def forward(self, real, fake, model):
gradient_penalty = self.compute_gradient_penalty(model, real, fake)
loss_real = torch.mean(model(real))
loss_fake = torch.mean(model(fake))
loss = -loss_real + loss_fake + gradient_penalty * self.lambda_gp
return loss, loss_real-loss_fake, gradient_penalty
def compute_gradient_penalty(self, model, real_samples, fake_samples):
alpha = torch.rand(real_samples.size(0), 1, 1, 1, device=self.device) # 生成一个张量值,值是在 [0, 1) 范围内随机
interpolates = (alpha * real_samples + ((1 - alpha) * fake_samples)).requires_grad_(True) # 线性插值生成样本并跟踪这个张量的梯度
d_interpolates = model(interpolates) #获取插值样本在生成器上的,以便计算梯度惩罚
gradients = autograd.grad(
outputs=d_interpolates,
inputs=interpolates,
grad_outputs=torch.ones(real_samples.size(0), d_interpolates.size(1)).to(self.device),
create_graph=True,
retain_graph=True,
only_inputs=True,
)[0]
gradients = gradients.view(gradients.size(0), -1)
gradient_penalty = ((gradients.norm(2, dim=1) - 1) ** 2).mean()
return gradient_penalty
判别器的损失函数在论文中描述到
A Wasserstein GAN (WGAN) with gradient penalty [14] has been proven to be robust of a wide variety of generator architectures. Considering the modified structure in our generator, we use Wasserstein loss with a gradient penalty to distinguish the real and generated velocity maps
- WGAN(Wasserstein GAN)
wasserstein距离:度量两个概率分布之间差异的距离度量。参考文章 - 判别器损失函数
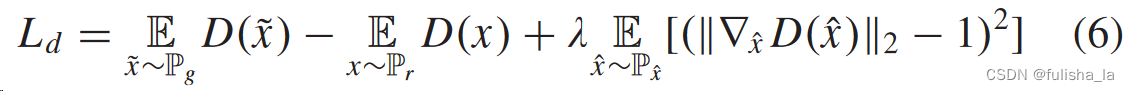
注:在GAN训练中,若把判别器训练得太好反而在实验中生成器会完全学不动。
P g P_g Pg生成器速度模型预测, P r P_r Pr真实速度模型预测, P x ^ P_{\hat{x}} Px^是 P g P_g Pg和 P r P_r Pr之间的随机样本, E D ( ⋅ ) ED(·) ED(⋅)代表判别器输出的期望值
- loss_real 真实样本在判别器上的损失的平均值
- loss_fake 生成样本在判别器上的损失的平均值
- gradient_penalty 梯度惩罚项
最后计判别器的损失函数
2.4 优化器
- Adam优化器
Adam算法是自适应学习率的优化算法,尤其在Transforms架构出现后,调整学习率是很困难的,使用SGD类似算法可能效果没有那么有用,采用Adam算法,结合了一阶矩阵动量和二阶矩阵动量来调整学习率。
input : γ (lr) , β 1 , β 2 (betas) , θ 0 (params) , f ( θ ) (objective) λ (weight decay) , amsgrad , maximize initialize : m 0 ← 0 ( first moment) , v 0 ← 0 (second moment) , v 0 ^ m a x ← 0 for t = 1 to … do if maximize : g t ← − ∇ θ f t ( θ t − 1 ) else g t ← ∇ θ f t ( θ t − 1 ) if λ ≠ 0 g t ← g t + λ θ t − 1 m t ← β 1 m t − 1 + ( 1 − β 1 ) g t v t ← β 2 v t − 1 + ( 1 − β 2 ) g t 2 m t ^ ← m t / ( 1 − β 1 t ) v t ^ ← v t / ( 1 − β 2 t ) if a m s g r a d v t ^ m a x ← m a x ( v t ^ m a x , v t ^ ) θ t ← θ t − 1 − γ m t ^ / ( v t ^ m a x + ϵ ) else θ t ← θ t − 1 − γ m t ^ / ( v t ^ + ϵ ) r e t u r n θ t \begin{aligned} &\rule{110mm}{0.4pt} \\ &\textbf{input} : \gamma \text{ (lr)}, \beta_1, \beta_2 \text{ (betas)},\theta_0 \text{ (params)},f(\theta) \text{ (objective)} \\ &\hspace{13mm} \lambda \text{ (weight decay)}, \: \textit{amsgrad}, \:\textit{maximize} \\ &\textbf{initialize} : m_0 \leftarrow 0 \text{ ( first moment)}, v_0\leftarrow 0 \text{ (second moment)},\: \widehat{v_0}^{max}\leftarrow 0\\[-1.ex] &\rule{110mm}{0.4pt} \\ &\textbf{for} \: t=1 \: \textbf{to} \: \ldots \: \textbf{do} \\ &\hspace{5mm}\textbf{if} \: \textit{maximize}: \\ &\hspace{10mm}g_t \leftarrow -\nabla_{\theta} f_t (\theta_{t-1}) \\ &\hspace{5mm}\textbf{else} \\ &\hspace{10mm}g_t \leftarrow \nabla_{\theta} f_t (\theta_{t-1}) \\ &\hspace{5mm}\textbf{if} \: \lambda \neq 0 \\ &\hspace{10mm} g_t \leftarrow g_t + \lambda \theta_{t-1} \\ &\hspace{5mm}m_t \leftarrow \beta_1 m_{t-1} + (1 - \beta_1) g_t \\ &\hspace{5mm}v_t \leftarrow \beta_2 v_{t-1} + (1-\beta_2) g^2_t \\ &\hspace{5mm}\widehat{m_t} \leftarrow m_t/\big(1-\beta_1^t \big) \\ &\hspace{5mm}\widehat{v_t} \leftarrow v_t/\big(1-\beta_2^t \big) \\ &\hspace{5mm}\textbf{if} \: amsgrad \\ &\hspace{10mm}\widehat{v_t}^{max} \leftarrow \mathrm{max}(\widehat{v_t}^{max}, \widehat{v_t}) \\ &\hspace{10mm}\theta_t \leftarrow \theta_{t-1} - \gamma \widehat{m_t}/ \big(\sqrt{\widehat{v_t}^{max}} + \epsilon \big) \\ &\hspace{5mm}\textbf{else} \\ &\hspace{10mm}\theta_t \leftarrow \theta_{t-1} - \gamma \widehat{m_t}/ \big(\sqrt{\widehat{v_t}} + \epsilon \big) \\ &\rule{110mm}{0.4pt} \\[-1.ex] &\bf{return} \: \theta_t \\[-1.ex] &\rule{110mm}{0.4pt} \\[-1.ex] \end{aligned} input:γ (lr),β1,β2 (betas),θ0 (params),f(θ) (objective)λ (weight decay),amsgrad,maximizeinitialize:m0←0 ( first moment),v0←0 (second moment),v0 max←0fort=1to…doifmaximize:gt←−∇θft(θt−1)elsegt←∇θft(θt−1)ifλ=0gt←gt+λθt−1mt←β1mt−1+(1−β1)gtvt←β2vt−1+(1−β2)gt2mt ←mt/(1−β1t)vt ←vt/(1−β2t)ifamsgradvt max←max(vt max,vt )θt←θt−1−γmt /(vt max+ϵ)elseθt←θt−1−γmt /(vt +ϵ)returnθt
γ \gamma γ:学习率; β 1 , β 2 \beta_1, \beta_2 β1,β2 第一个,第二个动量的指数衰减率; θ 0 \theta_0 θ0:模型参数的初始值; λ \lambda λ 权重衰减参数(控制参数更新的正则化项); maximize \textit{maximize} maximize:是否为最大化问题
初始化一阶动量 m 0 m_0 m0和二阶动量 v 0 v_0 v0为0, 在每次迭代中,计算梯度 g t g_t gt,若 λ \lambda λ 不为0将其添加到梯度中,更新一阶动量 m t m_t mt和二阶动量 v t v_t vt,再对一阶动量 m t m_t mt和二阶动量 v t v_t vt进行偏差矫正。(为什么要进行偏差矫正? 因为在初始化时一阶动量 m 0 m_0 m0和二阶动量 v 0 v_0 v0为0,会导致一阶动量和二阶动量的估计存在较大的偏差,影响到优化算法的收敛速度和稳定性,故加入了偏差矫正项 1 − β 1 t 1-\beta_{1}^{t} 1−β1t和 1 − β 2 t 1-\beta_{2}^{t} 1−β2t, 随着迭代次数增加,偏差矫正项逐渐减小) - AdamW优化器
AdamW算法相比于Adam算法,引入更加稳定的权重衰减方式,AdamW 在计算梯度时会将权重衰减项直接加到梯度上,而不是像 Adam 算法那样在参数更新时再单独处理。在VelocityGan中,优化器采用了AdamW优化器进行参数优化
input : γ (lr) , β 1 , β 2 (betas) , θ 0 (params) , f ( θ ) (objective) , ϵ (epsilon) λ (weight decay) , amsgrad , maximize initialize : m 0 ← 0 (first moment) , v 0 ← 0 ( second moment) , v 0 ^ m a x ← 0 for t = 1 to … do if maximize : g t ← − ∇ θ f t ( θ t − 1 ) else g t ← ∇ θ f t ( θ t − 1 ) θ t ← θ t − 1 − γ λ θ t − 1 m t ← β 1 m t − 1 + ( 1 − β 1 ) g t v t ← β 2 v t − 1 + ( 1 − β 2 ) g t 2 m t ^ ← m t / ( 1 − β 1 t ) v t ^ ← v t / ( 1 − β 2 t ) if a m s g r a d v t ^ m a x ← m a x ( v t ^ m a x , v t ^ ) θ t ← θ t − γ m t ^ / ( v t ^ m a x + ϵ ) else θ t ← θ t − γ m t ^ / ( v t ^ + ϵ ) r e t u r n θ t \begin{aligned} &\rule{110mm}{0.4pt} \\ &\textbf{input} : \gamma \text{(lr)}, \: \beta_1, \beta_2 \text{(betas)}, \: \theta_0 \text{(params)}, \: f(\theta) \text{(objective)}, \: \epsilon \text{ (epsilon)} \\ &\hspace{13mm} \lambda \text{(weight decay)}, \: \textit{amsgrad}, \: \textit{maximize} \\ &\textbf{initialize} : m_0 \leftarrow 0 \text{ (first moment)}, v_0 \leftarrow 0 \text{ ( second moment)}, \: \widehat{v_0}^{max}\leftarrow 0 \\[-1.ex] &\rule{110mm}{0.4pt} \\ &\textbf{for} \: t=1 \: \textbf{to} \: \ldots \: \textbf{do} \\ &\hspace{5mm}\textbf{if} \: \textit{maximize}: \\ &\hspace{10mm}g_t \leftarrow -\nabla_{\theta} f_t (\theta_{t-1}) \\ &\hspace{5mm}\textbf{else} \\ &\hspace{10mm}g_t \leftarrow \nabla_{\theta} f_t (\theta_{t-1}) \\ &\hspace{5mm} \theta_t \leftarrow \theta_{t-1} - \gamma \lambda \theta_{t-1} \\ &\hspace{5mm}m_t \leftarrow \beta_1 m_{t-1} + (1 - \beta_1) g_t \\ &\hspace{5mm}v_t \leftarrow \beta_2 v_{t-1} + (1-\beta_2) g^2_t \\ &\hspace{5mm}\widehat{m_t} \leftarrow m_t/\big(1-\beta_1^t \big) \\ &\hspace{5mm}\widehat{v_t} \leftarrow v_t/\big(1-\beta_2^t \big) \\ &\hspace{5mm}\textbf{if} \: amsgrad \\ &\hspace{10mm}\widehat{v_t}^{max} \leftarrow \mathrm{max}(\widehat{v_t}^{max}, \widehat{v_t}) \\ &\hspace{10mm}\theta_t \leftarrow \theta_t - \gamma \widehat{m_t}/ \big(\sqrt{\widehat{v_t}^{max}} + \epsilon \big) \\ &\hspace{5mm}\textbf{else} \\ &\hspace{10mm}\theta_t \leftarrow \theta_t - \gamma \widehat{m_t}/ \big(\sqrt{\widehat{v_t}} + \epsilon \big) \\ &\rule{110mm}{0.4pt} \\[-1.ex] &\bf{return} \: \theta_t \\[-1.ex] &\rule{110mm}{0.4pt} \\[-1.ex] \end{aligned} input:γ(lr),β1,β2(betas),θ0(params),f(θ)(objective),ϵ (epsilon)λ(weight decay),amsgrad,maximizeinitialize:m0←0 (first moment),v0←0 ( second moment),v0 max←0fort=1to…doifmaximize:gt←−∇θft(θt−1)elsegt←∇θft(θt−1)θt←θt−1−γλθt−1mt←β1mt−1+(1−β1)gtvt←β2vt−1+(1−β2)gt2mt ←mt/(1−β1t)vt ←vt/(1−β2t)ifamsgradvt max←max(vt max,vt )θt←θt−γmt /(vt max+ϵ)elseθt←θt−γmt /(vt +ϵ)returnθt
ϵ \epsilon ϵ 用于数值稳定性的小常数,通常取一个很小的值(主要是避免避免分母为零的情况)
对于Adam算法,权重衰减项是在计算梯度后与梯度相加的;对于AdamW算法,权重衰减项是在更新模型参数之前与当前模型参数相乘。
2.5 代码
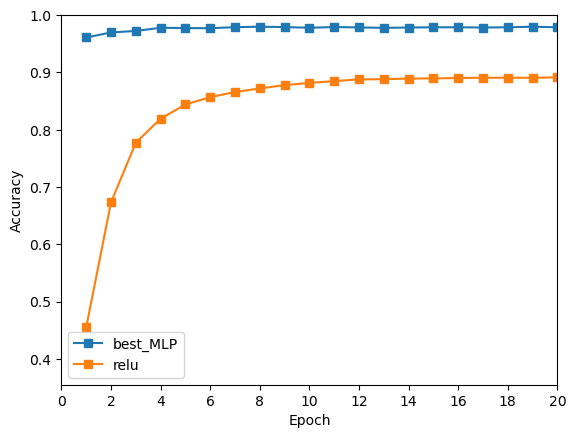
2.5.1 代码结果
因为是自己电脑上跑的,准备的训练数据集比较少,所以这个结果肯定不是很准确的。
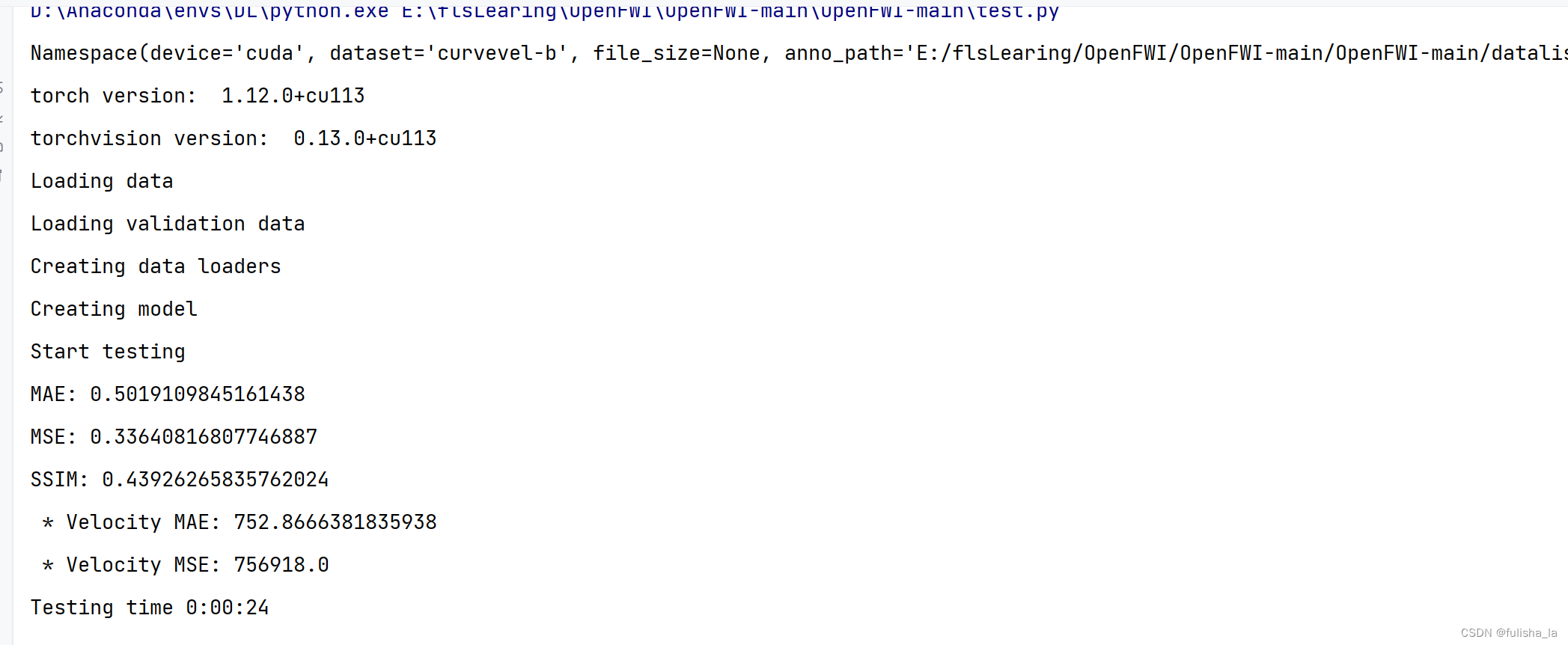
2.5.2 代码大致流程
训练网络结构(后续代码的一个大致流程):以gan_train.py为例
- 准备数据集:自定义的数据集FWIDataset,通过读取txt文件中的npy文件路径去下载数据集
- 建立数据加载器(数据加载器:为网络提供不同的加载形式)
- 搭建神经网络模型:在本论文的代码中,有两种网络模型,一种是生成器Generate(和InversionNet差不多,代码调用都一样),一种是判别器discriminater(是一种CNN神经网络结构)
- 创建损失函数 (生成器和判别器损失函数)
- 创建优化器 (采用的AdamW优化算法)
- 训练模型
- 测试模型
- 模型保存
4. 总结及收获
- 更为熟悉网络结构的一个完整流程。而我认为后续自己论文的主要出发点会在网络结构,损失函数和优化器上做创新。
- VelocityGan 是基于Gan网络进行的,在读完论文后,首先,VelocityGan的生成器和InversionNet的网络结构很相似。从最开始了解CNN一个传统的神经网络架构,主要就是卷积层,池化层到全连接层。到后续看到的一个FCN网络,将全连接层转换为卷积层,这样就可以保留空间的特征信息,添加反卷积层进行上采样,到后来了解到U-Net网络架构,一个对称的网络结构,也是一个端到端网络,U-Net的提出是在图像领域方面的,而后续看到我们研究内容相关的一些论文也是在这U-Net网络结构上进行创新,受到了很多启发(所以我们的确是可以去探索图像领域方面的优秀架构),如FCNVMB,他则是基于U-Net架构基础上创新。而我们看的这篇论文,他则可以说是在InversionNet网络架构的创新。 其次就是VelocityGan中的损失函数的设计,针对生成器和判别器,损失函数的设计不同,对于生成器,损失函数主要由对抗性损失和内容损失组成,对抗损失主要和判别器的判别结果有关,内容损失是和地质信息有关(主要是MSE和MSE); 对于判别器的损失函数主要是采用带有梯度惩罚的WGAN。最后优化器的选择,我想我更会倾向于ADAM和ADAMW中进行选择。
- 对于论文实验中提到各种模型的对比,以及在之前看论文中,都会有对比实验,而对比选择的模型是如何选择的?我不是很清楚。
4. 下周计划
- 主要任务是看这篇论文《Deep-Learning Full-Waveform Inversion Using Seismic Migration Images》
- 去看看图像相关论文的网络架构,学习一下。