案例2:构建自己的多层感知机: MNIST手写数字识别
相关知识点: numpy科学计算包,如向量化操作,广播机制等
1 任务目标
1.1 数据集简介
MNIST手写数字识别数据集是图像分类领域最常用的数据集之一,它包含60,000张训练图片,10,000张测试图片,图片中的数字均被缩放到同一尺寸且置于图像中央,图片大小为28×28。MNIST数据集中的每个样本都是一个大小为784×1的矩阵(从28×28转换得到)。MNIST数据集中的数字包括0到9共10类,如下图所示。注意,任何关于测试集的信息都不该被引入训练过程。

在本次案例中,我们将构建多层感知机来完成MNIST手写数字识别。
1.2 构建多层感知机
本次案例提供了若干初始代码,可基于初始代码完成案例,各文件简介如下:
(运行初始代码之前请自行安装TensorFlow 2.0及以上版本,仅用于处理数据集,禁止直接调用TensorFlow函数)
-
mlp.ipynb包含了本案例的主要内容,运行文件需安装Jupyter Noterbook. -
network.py定义了网络,包括其前向和后向计算。 -
optimizer.py定义了随机梯度下降(SGD),用于完成反向传播和参数更新。 -
solver.py定义了训练和测试过程需要用到的函数。 -
plot.py用来绘制损失函数和准确率的曲线图。
此外,在/criterion/和/layers/路径下使用模块化的思路定义了多个层,其中每个层均包含三个函数:__init__用来定义和初始化一些变量,
f
o
r
w
a
r
d
forward
forward和
b
a
c
k
w
a
r
d
backward
backward函数分别用来完成前向和后向计算:
-
FCLayer为全连接层,输入为一组向量(必要时需要改变输入尺寸以满足要求),与权重矩阵作矩阵乘法并加上偏置项,得到输出向量: u = W x + b u=Wx+b u=Wx+b -
SigmoidLayer为 s i g m o i d sigmoid sigmoid激活层,根据 f ( u ) = 1 1 + e − u f(u)=\frac{1}{1+e^{-u}} f(u)=1+e−u1计算输出。 -
ReLULayer为 R e L U ReLU ReLU激活层,根据 f ( u ) = m a x ( 0 , u ) f(u)=max(0,u) f(u)=max(0,u)计算输出。 -
EuclideanLossLayer为欧式距离损失层,计算各样本误差的平方和得到: 1 2 ∑ n ∣ ∣ l o g i t s ( n ) − g t ( n ) ∣ ∣ 2 2 \frac{1}{2}\sum_n||logits(n)-gt(n)||_2^2 21∑n∣∣logits(n)−gt(n)∣∣22。 -
SoftmaxCrossEntropyLossLayer可以看成是输入到如下概率分布的映射:
P ( t k = 1 / x ) = e X K ∑ j = 1 K e X j P(t_k=1/x)=\frac{e^{X_K}}{\sum_{j=1}^Ke^{X_j}} P(tk=1/x)=∑j=1KeXjeXK
其中 X k X_k Xk是输入向量X中的第k个元素, P ( t k = 1 / x ) P(t_k=1/x) P(tk=1/x)该输入被分到第 k k k个类别的概率。由于 s o f t m a x softmax softmax层的输出可以看成一组概率分布,我们可以计算delta似然及其对数形式,称为Cross Entropy误差函数:
E = − l n p ( t ( 1 ) , . . . , t ( N ) ) = ∑ n = 1 N E ( n ) E=-ln\ p(t^{(1)},...,t^{(N)})=\sum_{n=1}^NE^{(n)} E=−ln p(t(1),...,t(N))=n=1∑NE(n)
其中
E ( n ) = − ∑ k = 1 K t k ( n ) l n h k ( n ) h k ( n ) = P ( t k = 1 / X ( n ) ) = e X k ( n ) ∑ j = 1 K e X j ( n ) E^{(n)}=-\sum_{k=1}^Kt_k^{(n)}ln\ h_k{(n)}\\h_k^{(n)}=P(t_k=1/X^{(n)})=\frac{e^{X_k^{(n)}}}{\sum_{j=1}^Ke^{X_j^{(n)}}} E(n)=−k=1∑Ktk(n)ln hk(n)hk(n)=P(tk=1/X(n))=∑j=1KeXj(n)eXk(n)
注意:此处的softmax损失层与案例1中有所差异,本次案例中的softmax层不包含可训练的参数,这些可训练的参数被独立成一个全连接层。
1.3 案例要求
完成上述文件里的‘#TODO’部分(红色标记的文件),提交全部代码及一份案例报告,要求如下:
-
记录训练和测试准确率,绘制损失函数和准确率曲线图;
-
比较分别使用 S i g m o i d Sigmoid Sigmoid和 R e L U ReLU ReLU激活函数时的结果,可以从收敛情况、准确率等方面比较;
-
比较分别使用欧式距离损失和交叉熵损失时的结果;
-
构造具有两个隐含层的多层感知机,自行选取合适的激活函数和损失函数,与只有一个隐含层的结果相比较;
-
本案例中给定的超参数可能表现不佳,请自行调整超参数尝试取得更好的结果,记录下每组超参数的结果,并作比较和分析。
1.4 注意事项
-
提交所有代码和一份案例报告;
-
注意程序的运行效率,尽量使用矩阵运算,而不是for循环;
-
本案例中不允许直接使用TensorFlow, Caffe, PyTorch等深度学习框架;
-
禁止任何形式的抄袭。
2 代码设计
本节中介绍了代码整体架构,以及需要补全部分的函数设计。
2.1 数据处理
本实验进行MNIST手写数字识别,数据集采用 tensorflow 的tf.keras.datasets.mnist。
-
划分数据集
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data() -
数据预处理
decode_image()函数:对图像进行归一化处理。
该函数将图像的像素值转换为浮点数,然后将图像的形状变为一维的向量,最后将图像的像素值缩放到 (0,1) 之间,并减去图像数据的均值,使得分布接近标准 正态分布 。
def decode_image(image): # 归一化处理 image = tf.cast(image, tf.float32) image = tf.reshape(image, [784]) image = image / 255.0 image = image - tf.reduce_mean(image) return image-
decode_label()函数:将标签变为one-hot编码。该函数将标签的值转换为一个长度为10的向量,其中只有一个元素为1,其余为0,表示标签的类别。
def decode_label(label): # 将标签变为one-hot编码 return tf.one_hot(label, depth=10) -
数据预处理:对训练集和测试集的图像和标签进行了预处理。
将处理后的图像和标签合并为一个数据集,每个元素是一个元组,包含了一个图像和一个标签。
# 数据预处理 x_train = tf.data.Dataset.from_tensor_slices(x_train).map(decode_image) y_train = tf.data.Dataset.from_tensor_slices(y_train).map(decode_label) data_train = tf.data.Dataset.zip((x_train, y_train)) x_test = tf.data.Dataset.from_tensor_slices(x_test).map(decode_image) y_test = tf.data.Dataset.from_tensor_slices(y_test).map(decode_label) data_test = tf.data.Dataset.zip((x_test, y_test))
-
超参数设置
本实验中,采用了如下超参数,并对其设置了初值。
batch_size = 100 max_epoch = 20 init_std = 0.01 learning_rate_SGD = 0.001 weight_decay = 0.1 disp_freq = 50batch_size:表示每次训练时使用的数据样本的数量。max_epoch:表示训练的最大轮数。init_std:表示模型参数的初始化标准差,本次实验并未使用。learning_rate_SGD:表示随机梯度下降(SGD)优化器的学习率。weight_decay:表示权重衰减的系数。disp_freq:表示显示训练信息的频率,也就是每训练多少个批次就打印一次训练指标。
2.2 代码补全
-
optmizer.py
该代码实现了一个随机梯度下降(SGD)优化器,用于更新神经网络模型的参数。需要补全的地方是更新梯度的部分,此处代码如下。
# 计算梯度更新的变化量 layer.diff_W = - self.learningRate * (layer.grad_W + self.weightDecay * layer.W) layer.diff_b = - self.learningRate * layer.grad_b # 更新权重和偏置项 layer.W += layer.diff_W layer.b += layer.diff_b多层感知机梯度更新公式如下:
w n e w = w o l d − α ( ∇ J ( w ) + λ w o l d ) b n e w = b o l d − α ∇ J ( b ) w_{new}=w_{old}-\alpha (\nabla J(w)+ \lambda w_{old})\\ b_{new}=b_{old}-\alpha \nabla J(b) wnew=wold−α(∇J(w)+λwold)bnew=bold−α∇J(b)
其中 α \alpha α 是学习率, ∇ J ( θ ) \nabla J(\theta) ∇J(θ) 是梯度, λ \lambda λ 是权重衰减的系数。 -
fc_layer.py
该代码实现了一个全连接层,用于完全连接前后不同的神经元数的两层。
-
前向传播(
def forward())对输入进行线性变换 Y = W X + b Y=WX+b Y=WX+b ,然后返回输出。
def forward(self, Input): """ 对输入计算Wx+b并返回结果 """ self.input = Input return np.dot(Input, self.W) + self.b -
反向传播(
def backward())根据输出的梯度来计算输入的梯度和权重和偏置的梯度,然后返回输入的梯度。
KaTeX parse error: Undefined control sequence: \part at position 9: \frac {\̲p̲a̲r̲t̲ ̲E^{(n)}}{\part …
代码如下:def backward(self, delta): """ 根据delta计算梯度 """ self.grad_W = np.dot(self.input.T, delta) self.grad_b = np.sum(delta, axis=0, keepdims=True) delta = np.dot(delta, self.W.T) return delta
-
-
sigmoid_layer.py
该代码实现了一个基于 sigmoid 激活函数的激活层。
-
前向传播(
def forward(self, Input))对输入进行 Sigmoid 激活函数的处理,然后返回输出。
f ( x ) = 1 1 + e − x f(x) = \frac{1}{1+e^{-x}} f(x)=1+e−x1
代码如下:def forward(self, Input): """ 对输入应用Sigmoid激活函数并返回结果 """ self.output = 1 / (1 + np.exp(-Input)) return self.output -
反向传播(
def backward(self, delta))根据输出的梯度来计算输入的梯度,然后返回输入的梯度。
f ′ ( z ) = f ( z ) ( 1 − f ( z ) ) f^\prime (z)=f(z)(1-f(z)) f′(z)=f(z)(1−f(z))
代码如下:def backward(self, delta): """ 根据delta计算梯度 """ return delta * self.output * (1 - self.output)
-
-
relu_layer.py
该代码实现了一个基于 Relu 激活函数的激活层。
-
前向传播(
def forward(self, Input))对输入进行 Relu 激活函数的处理,然后返回输出。
f ( z ) = m a x ( 0 , z ) f(z)=max(0,z) f(z)=max(0,z)
代码如下:def forward(self, Input): """ 对输入应用ReLU激活函数并返回结果 """ self.input = Input return np.maximum(0, Input) -
反向传播(
def backward(self, delta))根据输出的梯度来计算输入的梯度,然后返回输入的梯度。
f ′ ( z ) = { 1 , i f z ≥ 0 0 , e l s e f^\prime (z)=\begin{cases}1,if\ z≥0\\0,else\end{cases} f′(z)={1,if z≥00,else
代码如下:def backward(self, delta): """ 根据delta计算梯度 """ return delta * (self.input > 0)
-
-
euclidean_loss.py
该代码实现了一个欧氏距离损失层。
-
前向传播(
def forward(self, logit, gt))对输出和真实标签之间的欧式距离损失进行计算,并返回损失值。它接受两个参数,
logit:表示最后一个全连接层的输出结果;gt:表示真实标签。
L ( y , f ( x ) ) = 1 2 n ∑ i = 1 n ( y i − f ( x i ) ) 2 L(\mathbf{y}, \mathbf{f}(\mathbf{x})) = \frac{1}{2n} \sum_{i=1}^n (\mathbf{y}_i - \mathbf{f}(\mathbf{x}_i))^2 L(y,f(x))=2n1i=1∑n(yi−f(xi))2
代码如下:def forward(self, logit, gt): """ 输入: (minibatch) - logit: 最后一个全连接层的输出结果, 尺寸(batch_size, 10) - gt: 真实标签, 尺寸(batch_size, 10) """ # 计算欧式距离损失 self.logit = logit self.diff = logit - gt self.loss = 0.5 * np.sum(self.diff ** 2) / logit.shape[0] # 计算平均损失 self.acc = np.sum(np.argmax(logit, axis=1) == np.argmax(gt, axis=1)) / logit.shape[0] # 计算平均准确率 return self.loss -
反向传播(
def backward(self))根据损失值的梯度来计算输出的梯度,并返回输出的梯度。
∂ L ∂ f ( x i ) = 1 n ( f ( x i ) − y i ) \frac{\partial L}{\partial \mathbf{f}(\mathbf{x}_i)} = \frac{1}{n}(\mathbf{f}(\mathbf{x}_i) - \mathbf{y}_i) ∂f(xi)∂L=n1(f(xi)−yi)
代码如下:def backward(self): # 欧式距离损失的梯度即为(logit - gt) / batch_size return self.diff / self.logit.shape[0]
-
-
softmax_cross_entropy.py
该代码实现了一个Softmax交叉熵损失层。
-
前向传播(
def forward(self, logit, gt))对输出和真实标签之间的Softmax交叉熵损失进行计算,并返回损失值。它接受两个参数,
logit:表示最后一个全连接层的输出结果;gt:表示真实标签。交叉熵损失函数:
E ( θ ) = − 1 n l n P ( t ( 1 ) , . . . , t ( n ) ) = − 1 n ∑ n = 1 n ( t ( n ) l n h ( x ( n ) + ( 1 − t ( n ) ) l n ( 1 − h ( x ( n ) ) ) E(θ)=-\frac{1}{n}lnP(t^{(1)},...,t^{(n)})=-\frac{1}{n}\sum^{n}_{n=1}\left(t^{(n)}ln\ h(x^{(n)}+(1-t^{(n)})ln\ (1-h(x^{(n)})\right)\\ E(θ)=−n1lnP(t(1),...,t(n))=−n1n=1∑n(t(n)ln h(x(n)+(1−t(n))ln (1−h(x(n)))
平均准确率:
a c c u r a c y = 正确分类的样本数 总样本数 \mathbf{accuracy} = \frac{\text{正确分类的样本数}}{\text{总样本数}} accuracy=总样本数正确分类的样本数
对logit和gt分别沿着第二个维度求最大值的索引,也就是得到每个样本的预测类别和真实类别,然后比较它们是否相等,得到一个一维布尔数组,表示每个样本是否正确分类。 然后,它对这个数组求和,得到一个标量,表示正确分类的样本数。然后,它除以
batch_size,得到一个标量,表示平均准确率,保存在self.acc中。代码如下:
def forward(self, logit, gt): """ 输入: (minibatch) - logit: 最后一个全连接层的输出结果, 尺寸(batch_size, 10) - gt: 真实标签, 尺寸(batch_size, 10) """ # 计算softmax激活函数 exp_logit = np.exp(logit - np.max(logit, axis=1, keepdims=True)) self.softmax_output = exp_logit / np.sum(exp_logit, axis=1, keepdims=True) # 计算交叉熵损失 self.loss = -np.sum(gt * np.log(self.softmax_output + EPS)) / logit.shape[0] # 计算平均准确率 self.acc = np.sum(np.argmax(logit, axis=1) == np.argmax(gt, axis=1)) / logit.shape[0] # 保存真实标签,用于反向传播 self.gt = gt return self.loss -
反向传播(
def backward(self))根据损失值的梯度来计算输出的梯度,并返回输出的梯度。
∇ E ( θ ) = 1 N ∑ N x ( n ) ( h ( x ( n ) ) − t ( n ) ) \nabla E(\theta)=\frac{1}{N}\sum_Nx^{(n)}(h(x^{(n)})-t^{(n)}) ∇E(θ)=N1N∑x(n)(h(x(n))−t(n))
代码如下:def backward(self): # 计算梯度 return np.subtract(self.softmax_output, self.gt) / self.gt.shape[0]
-
3 多层感知机训练
本实验分别使用了欧氏距离损失函数、Softmax交叉熵损失函数来训练具有唯一激活层的多层感知机,之后再以Softmax交叉熵作为损失函数,训练了具有两层隐含层的多层感知机。
3.1 使用欧氏距离损失训练多层感知机
-
使用 欧式距离损失 和 Sigmoid激活函数 训练多层感知机
本次训练采用3层感知机进行训练。
- 第一层为全连接层,将784个神经元的输入,转化为128个神经元的输出。
- 第二层采用 Sigmoid 激活层,为128个神经元进行非线性变换。
- 第三层为全连接层,将128个神经元的输入,转化为对应数字0到9的10个输出。
sigmoidMLP = Network() # 使用FCLayer和SigmoidLayer构建多层感知机 # 128为隐含层的神经元数目 sigmoidMLP.add(FCLayer(784, 128)) sigmoidMLP.add(SigmoidLayer()) sigmoidMLP.add(FCLayer(128, 10))训练结束后,在测试集上进行测试,准确率为 0.7810。
-
使用 欧式距离损失 和 Relu激活函数 训练多层感知机
本次训练采用3层感知机进行训练。
- 第一层为全连接层,将784个神经元的输入,转化为128个神经元的输出。
- 第二层采用 Relu 激活层,为128个神经元进行非线性变换。
- 第三层为全连接层,将128个神经元的输入,转化为对应数字0到9的10个输出。
reluMLP = Network() # 使用FCLayer和ReLULayer构建多层感知机 reluMLP.add(FCLayer(784, 128)) reluMLP.add(ReLULayer()) reluMLP.add(FCLayer(128, 10))训练结束后,在测试集上进行测试,准确率为 0.8586。
-
训练曲线对比
绘制了
loss曲线与acc曲线,对比以上两个感知机的训练结果。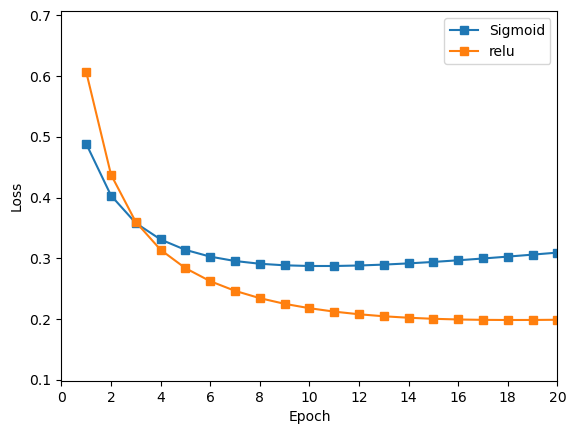
Sigmoid 的损失训练的初值低于 Relu,然而在训练过程中收敛效果不如 Relu,20轮训练后 Relu 损失更小。
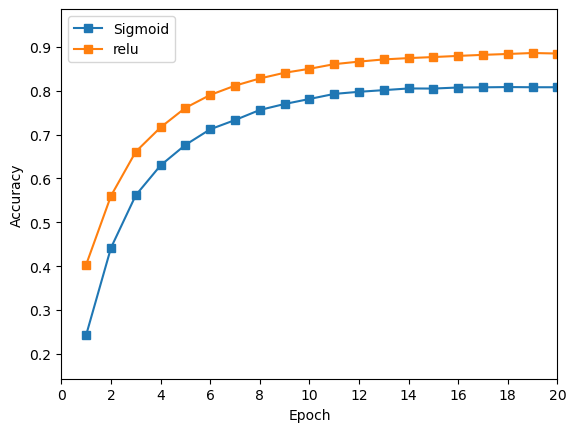
Relu 训练过程中的准确率始终高于 Sigmoid 的准确率。
由以上训练结果可知,在使用欧氏距离作为损失函数时,
Relu作为隐藏层激活函数效果好于Sigmoid函数。
3.2 使用Softmax交叉熵损失训练多层感知机
-
使用 Softmax交叉熵损失 和 Sigmoid激活函数 训练多层感知机
本次训练采用3层感知机进行训练。
- 第一层为全连接层,将784个神经元的输入,转化为128个神经元的输出。
- 第二层采用 Sigmoid 激活层,为128个神经元进行非线性变换。
- 第三层为全连接层,将128个神经元的输入,转化为对应数字0到9的10个输出。
# 使用FCLayer和SigmoidLayer构建多层感知机 # 128为隐含层的神经元数目 sigmoidMLP.add(FCLayer(784, 128)) sigmoidMLP.add(SigmoidLayer()) sigmoidMLP.add(FCLayer(128, 10))训练结束后,在测试集上进行测试,准确率为 0.6968。
-
使用 Softmax交叉熵损失 和 Relu激活函数 训练多层感知机
本次训练采用3层感知机进行训练。
- 第一层为全连接层,将784个神经元的输入,转化为128个神经元的输出。
- 第二层采用 Relu 激活层,为128个神经元进行非线性变换。
- 第三层为全连接层,将128个神经元的输入,转化为对应数字0到9的10个输出。
reluMLP = Network() # 使用FCLayer和ReLULayer构建多层感知机 reluMLP.add(FCLayer(784, 128)) reluMLP.add(ReLULayer()) reluMLP.add(FCLayer(128, 10))训练结束后,在测试集上进行测试,准确率为 0.8687。
-
训练曲线对比
绘制了
loss曲线与acc曲线,对比以上两个感知机的训练结果。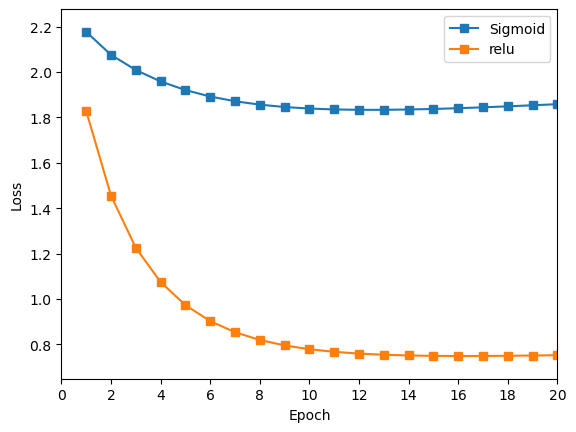
Sigmoid 的损失下降速率较慢,而 Relu 的损失下降明显更好,始终低于前者。
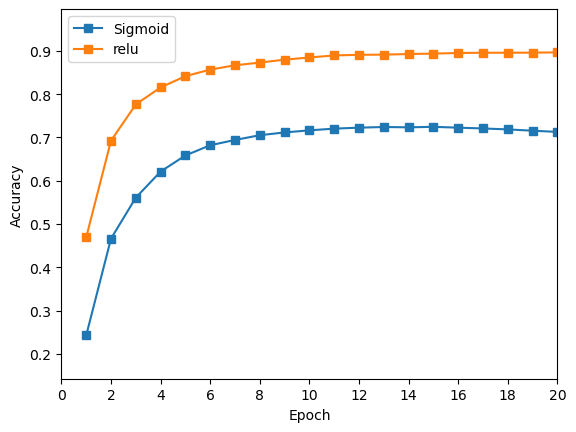
Relu 的准确率始终高于 Sigmoid,且 Relu+Softmax交叉损失 的组合较好于 Relu+欧氏距离损失 的组合,Sigmoid+Softmax交叉损失 的组合差于 Sigmoid+欧氏距离损失 的组合。
由以上训练结果可知,在使用Softmax交叉损失作为损失函数时,
Relu作为隐藏层激活函数效果好于Sigmoid函数;且好于用欧式距离作为损失函数的训练效果。
3.3 具有两层隐含层的多层感知机
本章中采用 Softmax交叉损失 作为损失函数,将 Relu 和 Sigmoid 组成四组组合,作为隐藏层的两层激活层,进行训练。
-
隐藏层为 两层Relu函数 的多层感知机
本次训练采用4层感知机进行训练。
- 第一层为全连接层,将784个神经元的输入,转化为128个神经元的输出。
- 第二层采用 Relu 激活层,为128个神经元进行非线性变换。
- 第三层采用 Relu 激活层,为128个神经元进行非线性变换。
- 第四层为全连接层,将128个神经元的输入,转化为对应数字0到9的10个输出。
relu2MLP = Network() # 128为隐含层的神经元数目 relu2MLP.add(FCLayer(784, 128)) relu2MLP.add(ReLULayer()) relu2MLP.add(ReLULayer()) relu2MLP.add(FCLayer(128, 10))训练结束后,在测试集上进行测试,准确率为 0.8696。
绘制曲线,与1层 Relu 进行对比。
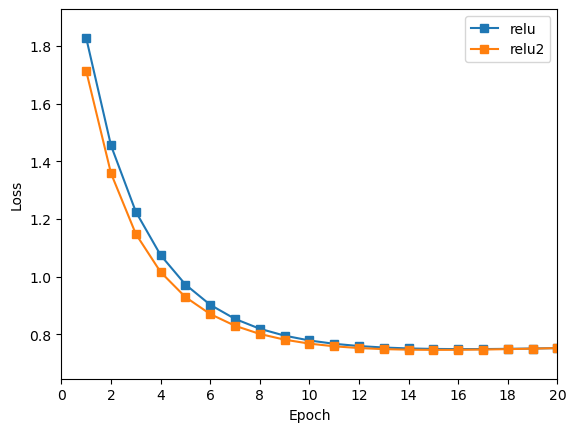
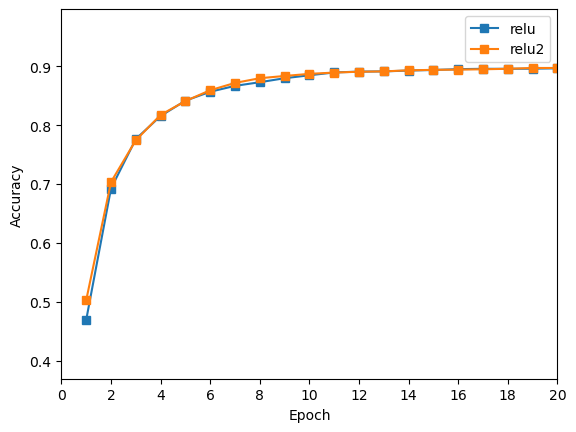
与1层
Relu对比,2层Relu训练效果略微提升,但是提升不大。 -
隐藏层为 两层Sigmoid函数 的多层感知机
本次训练采用4层感知机进行训练。
- 第一层为全连接层,将784个神经元的输入,转化为128个神经元的输出。
- 第二层采用 Sigmoid 激活层,为128个神经元进行非线性变换。
- 第三层采用 Sigmoid 激活层,为128个神经元进行非线性变换。
- 第四层为全连接层,将128个神经元的输入,转化为对应数字0到9的10个输出。
sigmoid2MLP = Network() # 128为隐含层的神经元数目 sigmoid2MLP.add(FCLayer(784, 128)) sigmoid2MLP.add(SigmoidLayer()) sigmoid2MLP.add(SigmoidLayer()) sigmoid2MLP.add(FCLayer(128, 10))训练结束后,在测试集上进行测试,准确率为 0.1137。
绘制曲线,与1层 Sigmoid 进行对比。
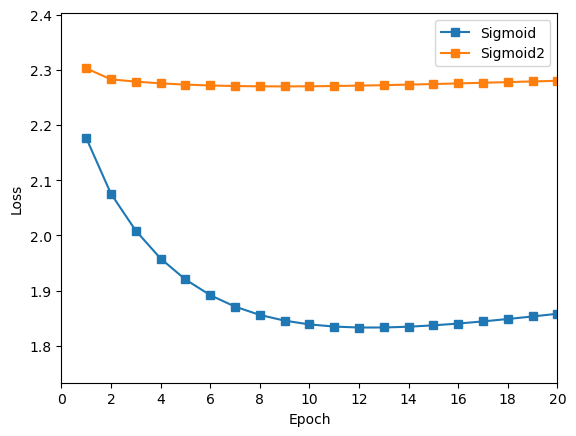
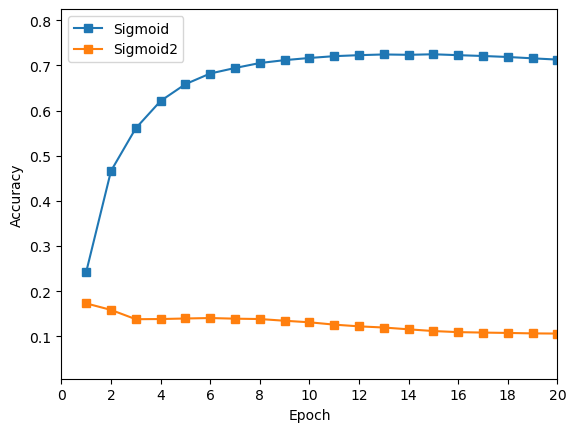
在使用两层
Sigmoid作为隐藏层时,训练结果极差,出现了梯度消失的现象。在训练两轮之后,Loss值不再降低,准确率不再提升。 -
隐藏层 先为Relu层,后为Sigmoid层 的多层感知机
本次训练采用4层感知机进行训练。
- 第一层为全连接层,将784个神经元的输入,转化为128个神经元的输出。
- 第二层采用 Relu 激活层,为128个神经元进行非线性变换。
- 第三层采用 Sigmoid 激活层,为128个神经元进行非线性变换。
- 第四层为全连接层,将128个神经元的输入,转化为对应数字0到9的10个输出。
ReluSigmoidMLP = Network() # 128为隐含层的神经元数目 ReluSigmoidMLP.add(FCLayer(784, 128)) ReluSigmoidMLP.add(ReLULayer()) ReluSigmoidMLP.add(SigmoidLayer()) ReluSigmoidMLP.add(FCLayer(128, 10))训练结束后,在测试集上进行测试,准确率为 0.6315。
-
隐藏层 先为Sigmoid层,后为Relu层 的多层感知机
本次训练采用4层感知机进行训练。
- 第一层为全连接层,将784个神经元的输入,转化为128个神经元的输出。
- 第二层采用 Sigmoid 激活层,为128个神经元进行非线性变换。
- 第三层采用 Relu 激活层,为128个神经元进行非线性变换。
- 第四层为全连接层,将128个神经元的输入,转化为对应数字0到9的10个输出。
SigmoidReluMLP = Network() # 128为隐含层的神经元数目 SigmoidReluMLP.add(FCLayer(784, 128)) SigmoidReluMLP.add(SigmoidLayer()) SigmoidReluMLP.add(ReLULayer()) SigmoidReluMLP.add(FCLayer(128, 10))训练结束后,在测试集上进行测试,准确率为 0.6996。
绘制曲线,与 先为Relu层,后为Sigmoid层 的做对比。
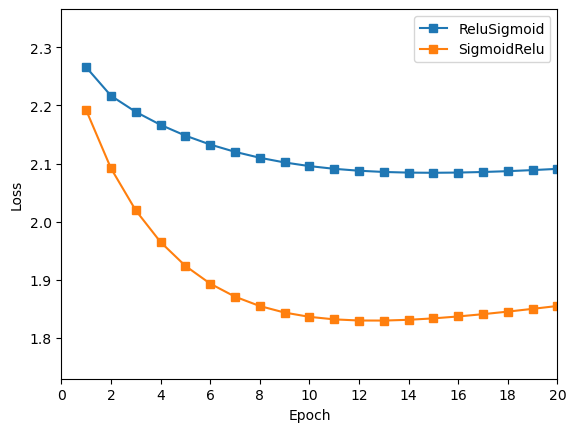
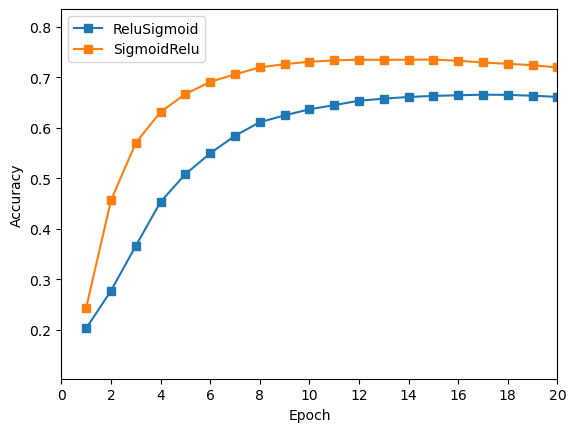
由上图可知,先
Sigmoid层,后Relu层的效果更好,但是两者效果都不如两层都是Relu的效果好。
4 寻找最佳超参数
本章通过遍历不同超参数,探索超参数对训练结果的影响,寻找最佳的超参数。
4.1 利用网格搜索寻找最佳超参数
编写代码,遍历超参数可能的取值,寻找最佳超参数。
from criterion import SoftmaxCrossEntropyLossLayer
from optimizer import SGD
from layers import FCLayer, ReLULayer
import itertools
import gc
# 定义超参数的可能取值
batch_sizes = [32,64,128]
max_epochs = [10,20,30]
learning_rates = [0.001, 0.005, 0.01]
weight_decays = [0.1, 0.01, 0.001]
# 保存最佳结果的变量
best_accuracy = 0.0
best_hyperparameters = {}
criterion = SoftmaxCrossEntropyLossLayer()
def build_and_train_model(batch_size, max_epoch, learning_rate, weight_decay):
sgd = SGD(learning_rate, weight_decay)
model = Network()
# 128为隐含层的神经元数目
model.add(FCLayer(784, 128))
model.add(ReLULayer())
model.add(ReLULayer())
model.add(FCLayer(128, 10))
model, model_loss, model_acc = train(model, criterion, sgd, data_train, max_epoch, batch_size, 1000)
return model, model_loss, model_acc
# 遍历所有超参数组合
for batch_size, max_epoch, learning_rate, weight_decay in itertools.product(
batch_sizes, max_epochs, learning_rates, weight_decays
):
# 构建和训练模型(使用当前超参数组合)
model, model_loss, model_acc = build_and_train_model(batch_size, max_epoch, learning_rate, weight_decay)
accuracy = test(model, criterion, data_test, batch_size, disp_freq)
# 如果当前组合的性能更好,则更新最佳结果
if accuracy > best_accuracy:
best_accuracy = accuracy
best_hyperparameters = {
'batch_size': batch_size,
'max_epoch': max_epoch,
'learning_rate': learning_rate,
'weight_decay': weight_decay
}
del model # 删除网络对象
gc.collect() # 执行垃圾回收
# 打印最佳结果
print("Best Hyperparameters:", best_hyperparameters)
print("Best Accuracy:", best_accuracy)
因为内存空间不足,未能跑完所有的超参数,在有限的内存中跑出的最佳参数,及测试结果如下。
Best Hyperparameters: {‘batch_size’: 32, ‘max_epoch’: 20, ‘learning_rate’: 0.005, ‘weight_decay’: 0.001} Best Accuracy: 0.9524238782051282
可以观察到,在batch_size选择较小值,训练轮次较大,学习率较高,权重衰减较小时,结果更好。
4.2 探寻学习率对训练结果的影响
编写代码,让模型分别在学习率为 [0.001, 0.005, 0.01] 的值训练,对比训练结果,寻找最佳的取值。
# 探寻学习率对训练结果的影响
from criterion import SoftmaxCrossEntropyLossLayer
from optimizer import SGD
from layers import FCLayer, ReLULayer
lrs = [0.001, 0.005, 0.01]
loss_lrs = []
acc_lrs = []
# 单层Relu,学习率0.1
criterion = SoftmaxCrossEntropyLossLayer()
for lr in lrs:
sgd = SGD(lr, 0.001)
model = Network()
# 128为隐含层的神经元数目
model.add(FCLayer(784, 128))
model.add(ReLULayer())
model.add(FCLayer(128, 10))
model, model_loss, model_acc = train(model, criterion, sgd, data_train, max_epoch, batch_size, 1000)
loss_lrs.append(model_loss)
acc_lrs.append(model_acc)
plot_loss_and_acc({'lr=0.001': [loss_lrs[0], acc_lrs[0]],
'lr=0.005': [loss_lrs[1], acc_lrs[1]],
'lr=0.01': [loss_lrs[2], acc_lrs[2]]})
训练结果:
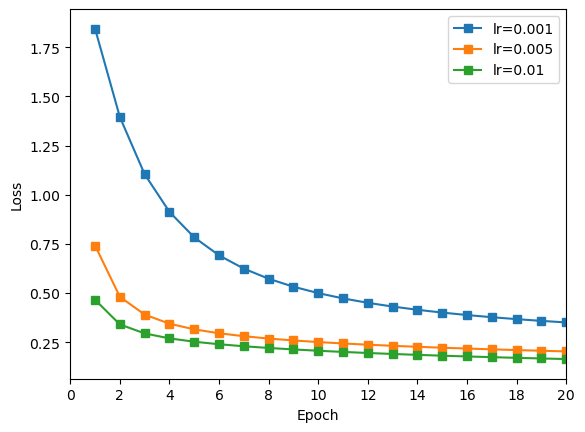
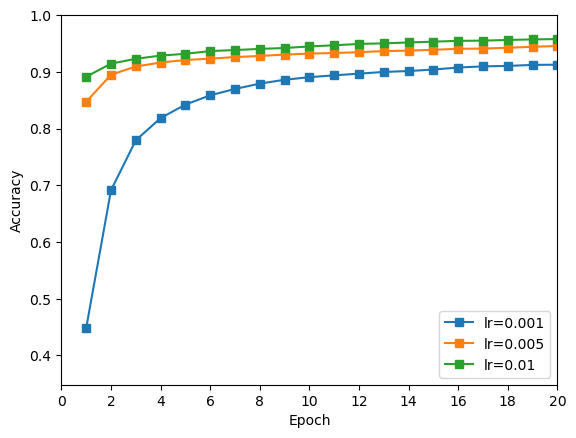
由上图可知,学习率越高,训练结果越好,其中学习率为 0.01 时训练效果最好。
4.3 探寻权重衰减对训练效果的影响
编写代码,让模型分别在权重衰减为 [0.001, 0.005, 0.01] 的值训练,对比训练结果,寻找最佳的取值。
# 探寻权重衰减对训练效果的影响
from criterion import SoftmaxCrossEntropyLossLayer
from optimizer import SGD
from layers import FCLayer, ReLULayer
wds = [0.001, 0.005, 0.01]
loss_wds = []
acc_wds = []
criterion = SoftmaxCrossEntropyLossLayer()
for wd in wds:
sgd = SGD(0.005, wd)
model = Network()
# 128为隐含层的神经元数目
model.add(FCLayer(784, 128))
model.add(ReLULayer())
model.add(FCLayer(128, 10))
model, model_loss, model_acc = train(model, criterion, sgd, data_train, max_epoch, batch_size, 1000)
loss_wds.append(model_loss)
acc_wds.append(model_acc)
plot_loss_and_acc({'wd=0.001': [loss_wds[0], acc_wds[0]],
'wd=0.005': [loss_wds[1], acc_wds[1]],
'wd=0.01': [loss_wds[2], acc_wds[2]]})
训练结果:
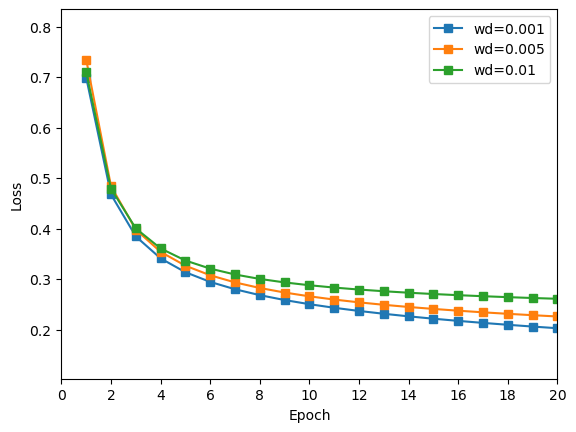
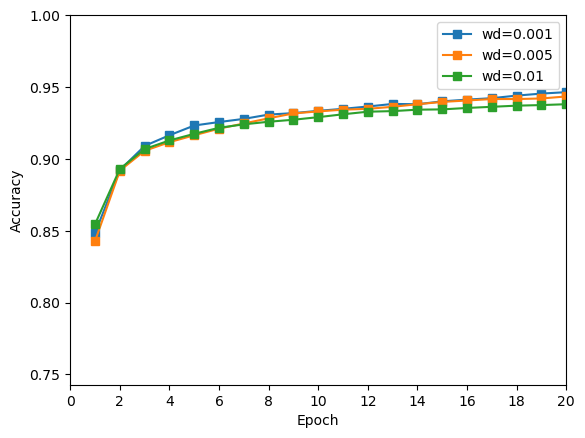
由上图可知,权重衰减值越小,训练结果最好,其中权重衰减值为 0.001 时结果最好。
4.4 探寻batch_size对训练效果的影响
编写代码,让模型分别在batch_size为 [32, 64, 128] 的值训练,对比训练结果,寻找最佳的取值。
# 探寻batch_size对训练效果的影响
from criterion import SoftmaxCrossEntropyLossLayer
from optimizer import SGD
from layers import FCLayer, ReLULayer
bss = [32, 64, 128]
loss_bss = []
acc_bss = []
criterion = SoftmaxCrossEntropyLossLayer()
for bs in bss:
sgd = SGD(0.01, 0.001)
model = Network()
# 128为隐含层的神经元数目
model.add(FCLayer(784, 128))
model.add(ReLULayer())
model.add(FCLayer(128, 10))
model, model_loss, model_acc = train(model, criterion, sgd, data_train, max_epoch, bs, 1000)
loss_bss.append(model_loss)
acc_bss.append(model_acc)
plot_loss_and_acc({'batch_size=32': [loss_bss[0], acc_bss[0]],
'batch_size=64': [loss_bss[1], acc_bss[1]],
'batch_size=128': [loss_bss[2], acc_bss[2]]})
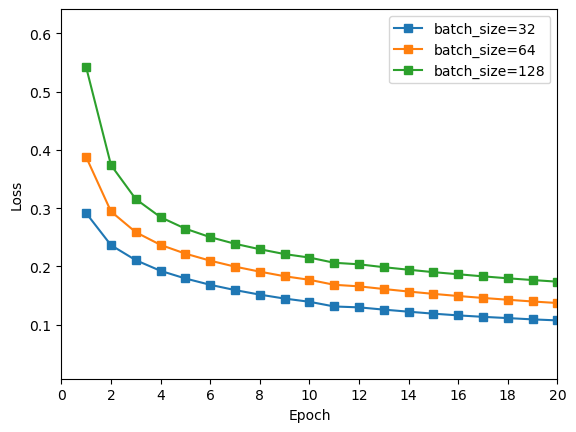
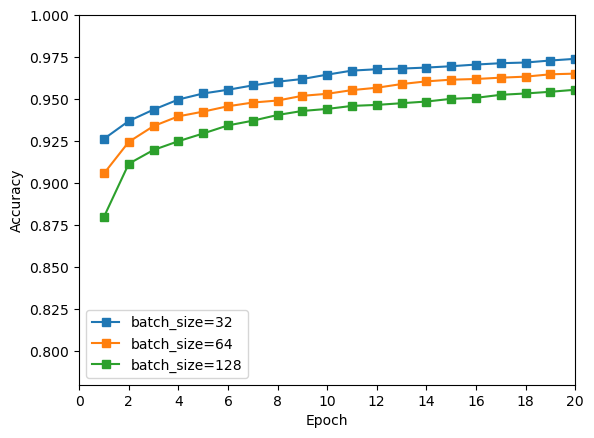
由上图可知,batch size 越小,训练效果越好,其中 batch size = 32 时训练效果最好。
4.5 测试最佳多层感知机
根据以上研究,我选取了以下超参数,作为本次实验找到的最佳超参数,并选取了 Softmax交叉熵 作为损失函数,两层 Relu 作为隐藏层进行测试,得到的结果即为本实验训练出的最佳多层感知机。
batch size = 32:每批次选取32张图片进行训练。max epoch = 50:进行50轮迭代训练。learning rate = 0.1:学习率设置为0.1。weight decay = 0.001:权重衰减设置为0.001。
# 最佳训练超参数
from criterion import SoftmaxCrossEntropyLossLayer
from optimizer import SGD
from layers import FCLayer, ReLULayer
batch_size = 32
max_epoch = 50
learning_rate_SGD = 0.1
weight_decay = 0.001
disp_freq = 1000
criterion = SoftmaxCrossEntropyLossLayer()
sgd = SGD(learning_rate_SGD, weight_decay)
Best_model = Network()
# 128为隐含层的神经元数目
Best_model.add(FCLayer(784, 128))
Best_model.add(ReLULayer())
Best_model.add(ReLULayer())
Best_model.add(FCLayer(128, 10))
Best_model, Best_model_loss, Best_model_acc = train(Best_model, criterion, sgd, data_train, max_epoch, batch_size, disp_freq)
test(Best_model, criterion, data_test, batch_size, disp_freq)
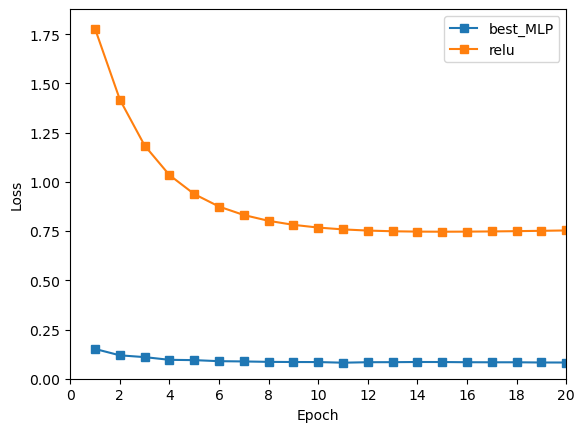
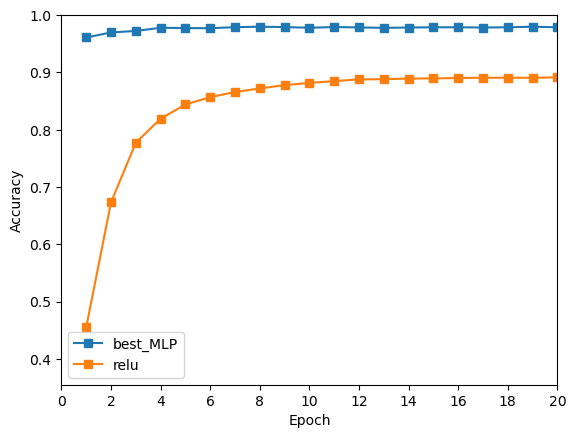
本实验得到的最佳多层感知机测试准确率为0.9759。
绘图对比这组超参数与之前训练较好的 Relu+Softmax交叉熵损失 组合,发现该组结果明显很好。