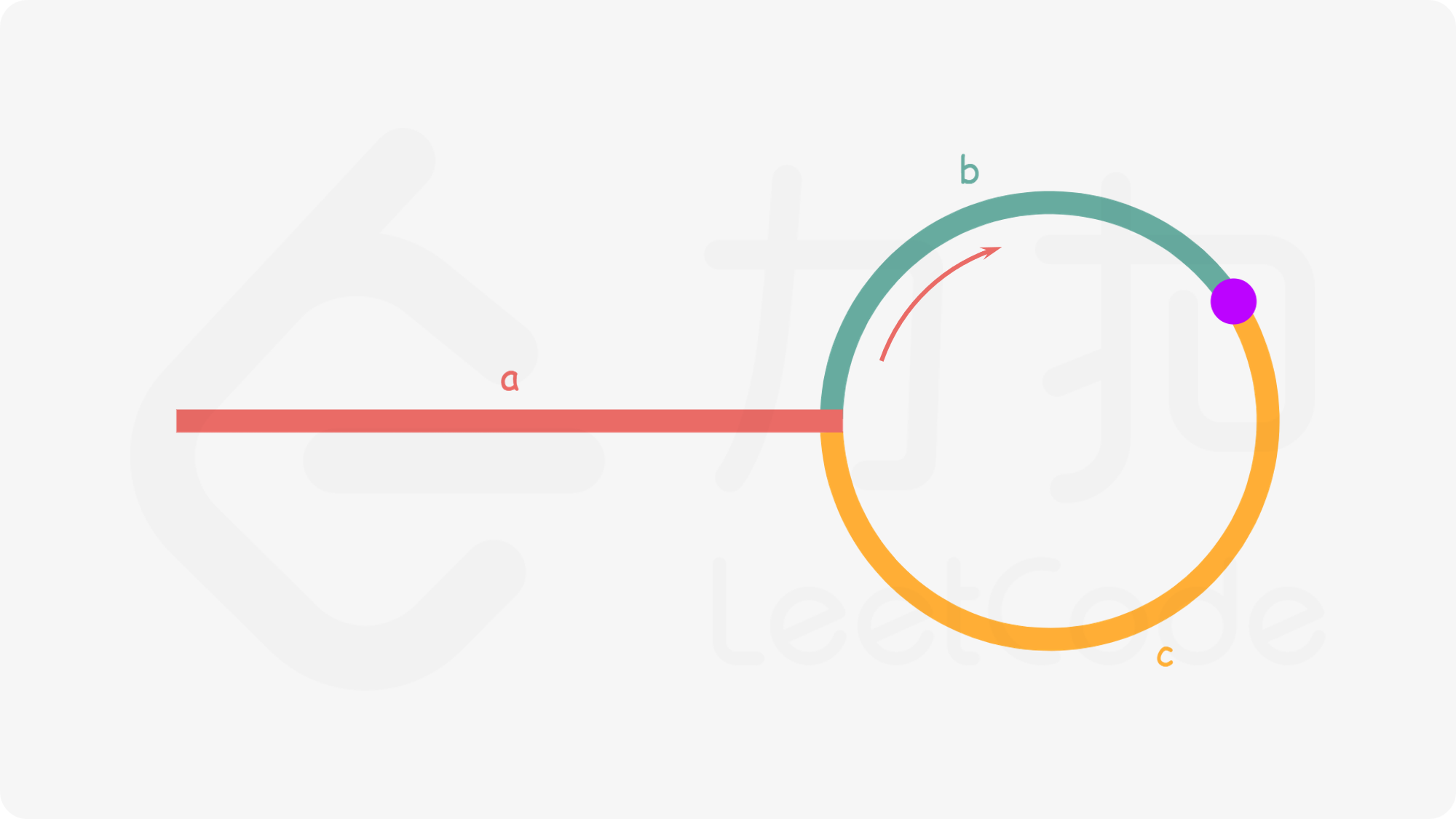论文地址：https://arxiv.org/abs/2002.05459
代码地址：https://github.com/CapsuleEndoscope/EndoL2H

论文小结

  顾名思义，本文是胶囊内窥镜领域的超分算法。本文的网络结构是条件对抗网络 + 空间attention块的方式，实现8倍、10倍和12倍的超分，方法的主要思路如下图所示。

  本文对比的方式仍为DBPN，RCAN和SRGAN等较为简单的方法，与这些方法进行了定性定量分析，来证明本文方法EndoL2H的优越性。由 30 名胃肠病学家进行的 MOS 测试定性评估并确认了该方法的临床相关性。

  本文设计了一种损失函数，名为高保真损失函数（High fidelity loss function），称为EndoL2H Loss，是专门针对内窥镜图像优化的加权混合损失函数。它协作地结合了感知、内容、纹理、基于像素的损失描述，并在像素值、内容和纹理方面提高图像质量。 即使在高达 10 -12 的极高比例因子下，这种组合也能保持图像质量。

  总的来说，值得参考的点在于不同损失函数之间的融合。至于实验内容，也是普通的高斯白噪声，以及高延时的图像超分算法。胶囊内窥镜只是说明其图像对象，并没有实时性相关要求。

论文介绍

  从HR图像到LR图像是要经过退化过程的。未知的退化过程，可能会收到散焦(defausing)、压缩伪影(compression artefacts)、各向异性退化(anisotropic degradations)、传感器噪声(sensor noise)、散斑噪声等各种因素的影响。本文的退化模型是集中退化因子的组合。

  本文的退化过程如下：在HR图像经过模糊核$\kappa$处理后，下采样，以及添加标准差为$\varsigma$的高斯白噪声。 D ( I H R ; δ ) = ( I H R ⊗ κ ) ↓ r + n ς ， { κ , r , ς } ⊂ δ (3) \mathcal{D}(I^{HR};\delta)=(I^{HR}\otimes \kappa)\downarrow_r+\mathcal{n}_\varsigma，\{\kappa,r,\varsigma \} \subset \delta \tag{3} D(IHR;δ)=(IHR⊗κ)↓r​+nς​，{κ,r,ς}⊂δ(3)

  本文所提出的网络架构EndoL2H如下图所示：由4个部分（生成器，空间注意力模块，判别器和混合目标函数）组成。

  空间注意力块如上面网络结构图b所示。在本文，空间注意力块（Spatial Attention Blcok，SAB）被放在了第一层卷积层后。

  生成器和判别器如上图a所示，是UNet结构的派生（带有大量的skip connection），其中带有一个额外的空间注意力块。将$Ck$定义为$k$个核的卷积层，BN层和ReLU层的堆叠，将$CDk$定义为$k$个核的卷积层，BN层，$50\%$概率的dropout层和ReLU层的堆叠。所有卷积层都是$4\ast 4$，空间核的stride为$2$。注意力U-Net编码器和注意力U-Net解码器的结构如下：然后在解码器的后面接一层卷积和$tanh$非线性层来将解码器的最后一层输出映射到需要的输出channel上。上述结构中还有一个例外，即编码器的第一个$C64$层没有BN层。编码器中的所有ReLU都是倾斜度$\alpha =0.2$的Leaky ReLU，而解码器中是没有倾斜度的。

  EndoL2H Loss将集中损失进行了结合。Per-Pixel Loss，衡量的是像素级别上的差异；GAN判别器是对高频结构进行建模，以确保输出更针织和有用的SR图像。与基于交叉熵的标准 GAN 目标不同，作者定义了基于最小二乘误差的 GAN 损失，从而提高训练期间的稳定性和训练结束时更好的收敛性。内容损失鼓励低频域中的感知相似性和一致性；纹理损失强调从退化的输入图像中重新捕获纹理信息。
  作者称，这种混合损失函数，EndoL2H 损失，是专门为内窥镜类型的图像设计和经验优化的，使其在标准和胶囊内窥镜图像超分辨率方面都是独一无二的。

  Per-Pixel Loss采用的是$L_1$损失的变体，为Charbonnier Loss，定义如下：其中$ϵ$是一个小值常量，比如$10^{-3}$。像素损失可以有更高的PSNR，但其有一个众所周知的缺点：它无法保持感知图像质量以及经常以过于平滑的纹理结束的高频信息。$${\mathcal{L}}_{Cha}(I^{SR},I^{HR})=\frac{1}{hwc}\sum _{i,j,k}\sqrt{(I_{i,j,k}^{SR}-I_{i,j,k}^{HR}{)}^2+{ϵ}^2}$$

  Content Loss.，也叫感知损失，是通过预训练的模型作为语义特征提取器进行评估的。本文使用带ReLU激活层的预训练VGG网络。对VGG提取的特征，使用欧式距离进行衡量。

  Texture Loss.应该是使用边缘检测等算子，对提取出来的特征进行处理，处理结果进行相应的举例衡量。$${\mathcal{L}}_{texture}(I^{SR},I^{HR},\varphi ,l)=\frac{1}{c_l^2}\sqrt{\sum _{i,j}(G_{i,j}^{(l)}(I^{SR})-G_{i,j}^{(l)}(I^{HR}){)}^2}$$

  Adversarial Loss.本文使用的对抗损失没有使用交叉熵损失，而是使用最小二乘误差。$${\mathcal{L}}_{adv}(I^{SR},I^{HR};D)=(D(I^{SR}){)}^2+(D(I^{HR})-1{)}^2$$

  EndoL2H Loss.，是数个损失的结合。$${\mathcal{L}}_{L2H}=\alpha \ast {\mathcal{L}}_{adv}+(1-\alpha )(1-\beta )(1-\gamma )\ast {\mathcal{L}}_{Cha}+\gamma \ast {\mathcal{L}}_{content}+\beta \ast {\mathcal{L}}_{texture}$$

论文实验

  本文使用的数据集来自原始的 Kvasir 数据集。在定量指标方面，应用了 PSNR、SSIM、LPIPS 和 GMSD。根据定性指标，进行了临床 MOS，其中 30 名胃肠病学家对来自测试数据集的 15 个随机采样图像进行了投票。
  GMSD指标，是从[58]引入的，是基于梯度的相似性方法家族的成员。

  原始的 Kvasir 数据，由80000张内窥镜图像组成，是由奥林巴斯和宾得的各种内窥镜设备记录，从不同的胃肠道器官获得，包括肠、胃、食道、十二指肠 (v2)[50]。10折划分法的每一个都由包含八个不同类别的测试和训练集组成：染色的息肉、染色的切除边缘、食管炎、正常盲肠、正常幽门、正常 z 线、息肉和溃疡性结肠炎。在这项研究中，作者删除了带有大绿色注释的图像样本，这些注释说明了所用内窥镜设备的位置和配置。 剩余数据集由 21220 张分辨率为 1280x1024 的图像组成，包含来自食管炎、正常幽门、正常 z 线、息肉和溃疡性结肠炎类的图像。

  制作超分数据集，使用双三次（bicubic）进行下采样，因子分别为8倍，10倍和12倍，以及添加额外的高斯核作为模糊核。前面讲一堆，后面还是只用了高斯噪声。

  训练使用Nvidia Tesla V100显卡。数据集分为三份：17,220张图像用于训练，2000张图像用户验证，2000张图像用于测试。EndoL2H使用$10^{-4}$的学习率训练$10^5$次迭代，然后使用$10^{-5}$的学习率训练$10^5$次迭代。Pytorch训练框架，Adam优化器，动量参数${\beta }_1=0.5,{\beta }_2=0.999$。

  下表是实验结果，其中EndoL2H-w/o-C是没有${\mathcal{L}}_{content}$，EndoL2H-w/o-T是没有${\mathcal{L}}_{texture}$。与EndoL2H-w/o-C相比，EndoL2H-w/o-T的定量结果都差不少，输出 SR 图像更平滑和更粗糙，揭示了 SR 的纹理损失的有效性。(如果将内窥镜图像进行分类，比如按食道炎、正常幽门、正常z线、息肉和溃疡性结肠炎分为5类，结果也差不多)。绝大多数情况下，EndoL2H-w/o-C都是优于EndoL2H-w/o-T的，这表明对于SR而言，纹理损失要比内容损失重要。

  使用混合损失函数时的一个重要挑战是控制参数优化的难度，它最终决定了哪个损失组件应该以何种程度对学习过程做出贡献。 为了最佳地确定 EndoL2H 损失权重，作者从数据集中随机抽取 3,000 张图像并生成 10 个不同的超参数集 { α , β , γ } \{\alpha, \beta, \gamma \} {α,β,γ}，实验结果如下表所示：$\alpha =0.35,\beta =0.20,\gamma =0.15$有最好的指标结果，4个指标同时达到最佳值。

  下表是4种超分算法在不同超分倍率下的运行时间对比，运行时间是在Nvidia Tesla V100 GPU上跑多次平均得到的。

  关于空间注意力块的消融学习，可以看出有明显的提升。