一【题目类别】

• 数学

二【题目难度】

• 中等

三【题目编号】

• 89.格雷编码

四【题目描述】

• n 位格雷码序列 是一个由 2n 个整数组成的序列，其中：
  • 每个整数都在范围 [0, 2n - 1] 内（含 0 和 2n - 1）
  • 第一个整数是 0
  • 一个整数在序列中出现 不超过一次
  • 每对 相邻 整数的二进制表示 恰好一位不同 ，且
  • 第一个 和 最后一个 整数的二进制表示 恰好一位不同
• 给你一个整数 n ，返回任一有效的 n 位格雷码序列 。

五【题目示例】

• 示例 1：

  • 输入：n = 2
  • 输出：[0,1,3,2]
  • 解释：
    • [0,1,3,2] 的二进制表示是 [00,01,11,10] 。
      • 00 和 01 有一位不同
      • 01 和 11 有一位不同
      • 11 和 10 有一位不同
      • 10 和 00 有一位不同
    • [0,2,3,1] 也是一个有效的格雷码序列，其二进制表示是 [00,10,11,01] 。
      • 00 和 10 有一位不同
      • 10 和 11 有一位不同
      • 11 和 01 有一位不同
      • 01 和 00 有一位不同

• 示例 2：

  • 输入：n = 1
  • 输出：[0,1]

六【解题思路】

• 本题所描述的格雷编码其实非常有名，要构造格雷编码首先要明白什么是格雷编码，至于这点题目描述已经说明的很详细了，不再赘述，我们要讨论的是其构造方法
• 其实也算不上什么算法，就是找规律，多写几个长度的格雷编码就可以找到规律了，我就不在这里写了，直接将规律总结如下：
  • n+1位的格雷编码的前$2^n$个码字为n位格林编码以顺序书写此编码序列的方式，在每个编码前面加数字0，其实相当于不变
  • n+1位的格雷编码的前$2^n$个码字为n位格林编码以顺序书写此编码序列的方式，在每个编码前面加二进制数字1，可以过移位得到
  • 那么n+1位格雷编码包括以上两种情况的并集
• 后面就可以根据以上思路进行代码的编写了，需要几位的格雷编码，只需要通过本位之前的格雷编码生成，具体操作可见代码，与上面思路无异
• 最后返回结果即可

七【题目提示】

• $1<=n<=16$

八【时间频度】

• 时间复杂度：$O(2^n)$，其中$n$为传入参数的大小
• 空间复杂度：$O(1)$，返回值不计入空间复杂度

九【代码实现】

1. Java语言版

class Solution {
    public List<Integer> grayCode(int n) {
        List<Integer> res = new ArrayList<>();
        res.add(0);
        int head = 1;
        for(int i = 1;i<=n;i++){
            for(int j = res.size() - 1;j>=0;j--){
                res.add(head + res.get(j));
            }
            head <<= 1;
        }
        return res;
    }
}

2. C语言版

int* grayCode(int n, int* returnSize)
{
    int* res = (int*)malloc(sizeof(int) * (1 << n));
    int len = 1 << n;
    res[0] = 0;
    int head = 1;
    int index = 1;
    for(int i = 1;i<=n;i++)
    {
        for(int j = index - 1;j>=0;j--)
        {
            res[index++] = head + res[j];
        }
        head <<= 1;
    }
    *returnSize = index;
    return res;
}

3. Python版

class Solution:
    def grayCode(self, n: int) -> List[int]:
        res = [0]
        head = 1
        for i in range(1,n+1):
            for j in range(len(res) - 1,-1,-1):
                res.append(head + res[j])
            head <<= 1
        return res

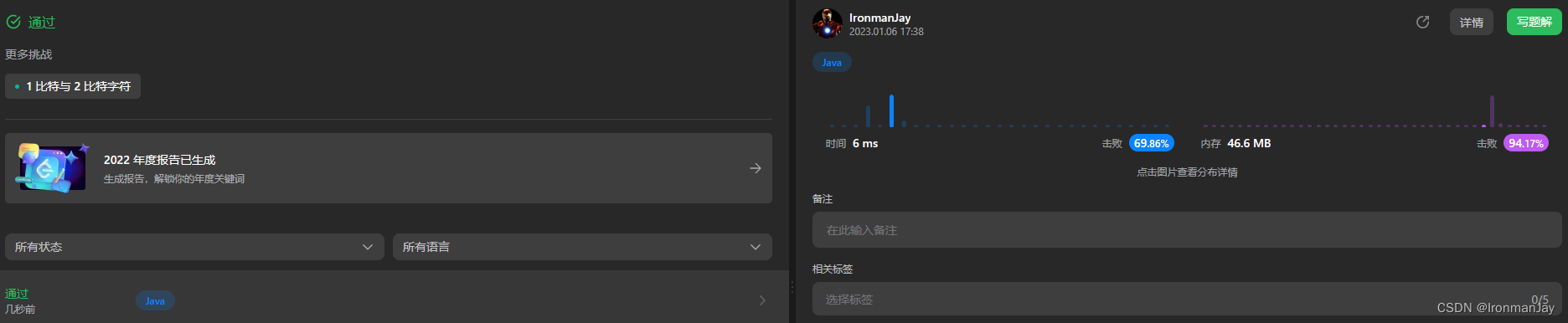
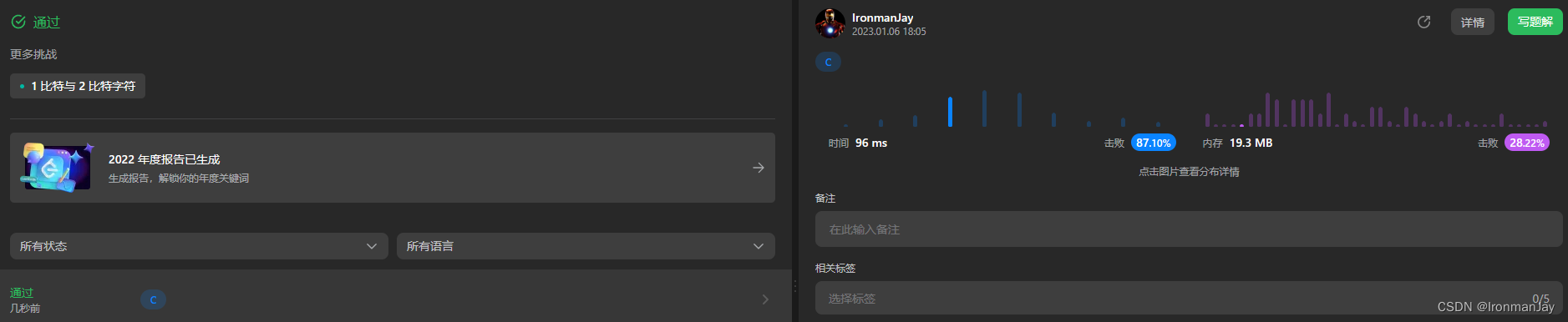
十【提交结果】

1. Java语言版
   

2. C语言版
   

3. Python语言版