一、删除链表中的倒数第n个节点

题目链接：19.删除链表中的倒数第n个节点

/**
 * <pre>
 * 最简单的方法显然是先遍历一遍链表，知道长度后重新遍历一次就可以找到指定节点了，由此方法我们不难延伸到另一种解法
 * 既然是删除倒数第n个节点，那么也就是一旦遇到最后一个节点那么它前面的第n个节点就是要删除的节点
 * 我们只要使用快慢指针，慢指针在快指针前n位，那么当快指针到达链表尾时慢指针所指的就是需要删除的节点
 * </pre>
 *
 * @author <a href="https://github.com/kil1ua">Ken-Chy129</a>
 * @date 2023/1/5 14:52
 */
public class 删除链表的倒数第N个结点19 {
    
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode pos1=new ListNode(), pos2=head, res = pos1;
        pos1.next = head;
        int i=0;
        while (pos2 != null) {
            if (i < n) { // 找的是链尾的前第n+1个，这样才能删除链尾的第n个
                i++;
            } else {
                pos1 = pos1.next;
            }
            pos2 = pos2.next;
        }
        pos1.next = pos1.next.next;
        return res.next;
    }

    public ListNode removeNthFromEnd2(ListNode head, int n) {
        ListNode p = new ListNode(), res = p;
        p.next = head;
        Deque<ListNode> stack = new LinkedList<>();
        while (p != null) {
            stack.push(p);
            p = p.next;
        }
        for (int i=0; i<n; i++) {
            stack.pop();
        }
        p = stack.peek();
        p.next = p.next.next;
        return res.next;
    }
}

二、链表相交

题目链接：160.链表相交

/**
 * <pre>
 * 计算出两个链表的长度，让长的链表先移动到和短的链表一样长（因为交点不可能在前面部分），随后两个链表同时移动，相等时即为交点
 * 或者使用哈希表将第一个链表的元素进行存储，然后遍历第二个链表判断当前节点是否存在在哈希表中
 * 两者时间复杂度相同，但是哈希表需要额外的空间开销（哈希表查找元素是需要O(1)的时间复杂度，所以总的时间开销相同）
 * </pre>
 *
 * @author <a href="https://github.com/kil1ua">Ken-Chy129</a>
 * @date 2023/1/6 13:49
 */
public class 链表相交160 {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode pa = headA, pb = headB;
        int lena=1, lenb=1;
        while (pa != null) {
            pa = pa.next;
            lena++;
        }
        while (pb != null) {
            pb = pb.next;
            lenb++;
        }
        pa = headA;
        pb = headB;
        if (lena > lenb) {
            for (int i=1; i<=lena-lenb; i++) {
                pa = pa.next;
            }
        } else if (lena < lenb) {
            for (int i = 1; i <= lenb - lena; i++) {
                pb = pb.next;
            }
        }
        while (pa != null) {
            if (pa == pb) {
                return pa;
            }
            pa = pa.next;
            pb = pb.next;
        }
        return null;
    }

    public ListNode getIntersectionNode2(ListNode headA, ListNode headB) {
        Set<ListNode> visited = new HashSet<ListNode>();
        ListNode temp = headA;
        while (temp != null) {
            visited.add(temp);
            temp = temp.next;
        }
        temp = headB;
        while (temp != null) {
            if (visited.contains(temp)) {
                return temp;
            }
            temp = temp.next;
        }
        return null;
    }
}

三、环形链表

题目链接：142.环形链表

/**
 * <pre>
 * 可以使用快慢指针的方式，让快指针每次走两格，慢指针每次走一格，快指针先入环而且一定会在环中与慢指针相遇
 * 因为在环中对于慢指针来说，其实快指针是以每次1的速度向他逼近，最终一定会碰上
 * </pre>
 *
 * @author <a href="https://github.com/kil1ua">Ken-Chy129</a>
 * @date 2023/1/6 14:26
 */
public class 环形链表II142 {
    public ListNode detectCycle(ListNode head) {
        ListNode pos1 = head, pos2 = head;
        while (pos2 != null) {
            if (pos2.next == null) {
                return null;
            }
            pos1 = pos1.next;
            pos2 = pos2.next.next;
            if (pos2 == pos1) {
                ListNode p = head;
                while (p != pos1) {
                    p = p.next;
                    pos1 = pos1.next;
                }
                return p;
            }
        }
        return null;
    }
}

注释中已经分析了如果有环为什么两个指针一定会在环中相遇，接下来分析一下如何寻找环的起点。

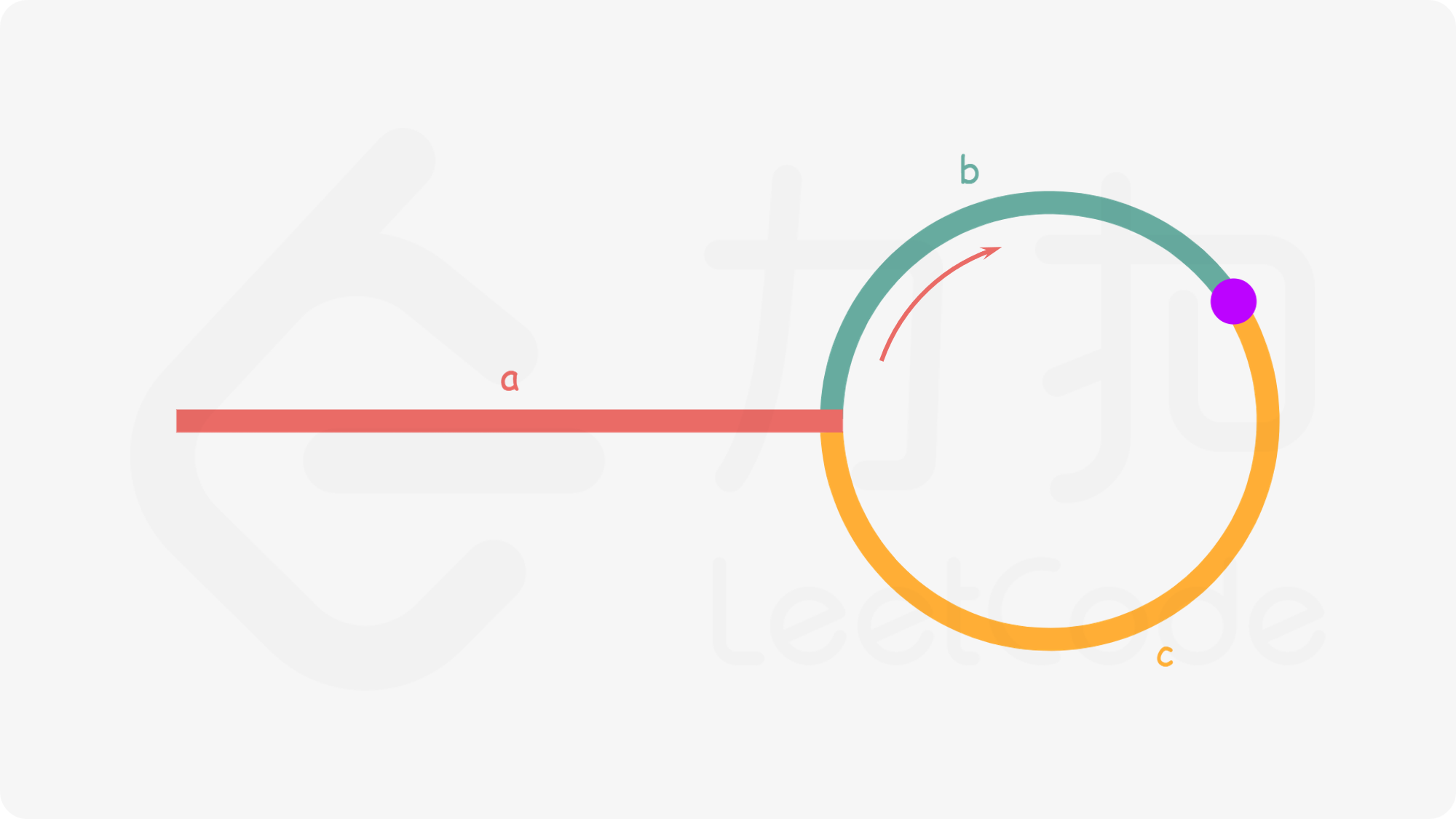
途中紫色点为快慢指针的相遇点，假设快指针走了n圈后与慢指针相遇，那么相遇时有：

• 快指针走的距离：a+n(b+c)+b
• 快指针走的距离是慢指针的两倍
• 慢指针走的距离：a+b
  • 为什么慢指针一定会在第一圈跟快指针相遇？
  • 其实在注释中也写到了，每次循环可以理解为快指针在以每次为1的速度追赶慢指针，而在慢指针进入环的时候快指针距离它的距离最多也是少于1圈（快指针在慢指针前一位时为最长距离），那么追赶到的时候慢指针必然没有进入下一圈
• 那么就有a+n(b+c)+b=2(a+b)，化简得a=c+(n-1)(b+c)，(n-1)(b+c)表示n-1圈，那么也就是说只要这时让一个指针从链表起点出发，另一个指针从快慢指针相遇点出发，那它们会正好在环的起点相遇（因为a的长度等于从快慢指针相交点绕环n-1圈后再走c的长度，而再走c的长度正好就是到环的起点）