目录
问题描述:
实现代码与解析:
直接当普通二叉树遍历:
利用完全二叉树和满二叉树的特性:
原理思路:
问题描述:
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
示例 1:
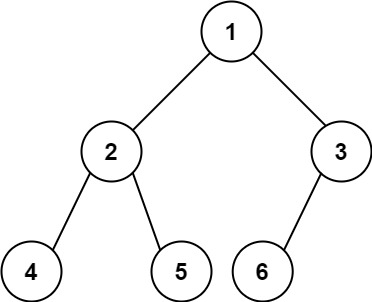
输入:root = [1,2,3,4,5,6] 输出:6
示例 2:
输入:root = [] 输出:0
示例 3:
输入:root = [1] 输出:1
实现代码与解析:
直接当普通二叉树遍历:
class Solution {
public:
void traveral(TreeNode* cur,vector<int>& result)
{
if(cur==NULL) return;
result.push_back(cur->val);
traveral(cur->left,result);
traveral(cur->right,result);
}
int countNodes(TreeNode* root)
{
vector<int> result;
traveral(root,result);
return result.size();
}
};这里可以用前中后序递归,非递归,层序遍历把结点放入数组中,然后计算数组大小即可。
当然也可以直接递归返回结点个数如:
class Solution {
public:
int countNodes(TreeNode* root)
{
if(root==NULL) return 0;
return countNodes(root->left)+countNodes(root->right)+1;
}
};上面的都是计算普通二叉树的结点方法,没有用到完全二叉树的知识,下面给出利用完全二
叉树解题的代码,同时给出解析。
利用完全二叉树和满二叉树的特性:
class Solution {
public:
int countNodes(TreeNode* root)
{
if(root==NULL) return 0;//终止条件
TreeNode* left=root->left;
TreeNode* right=root->right;
int leftDepth=0;//左子树深度
int rightDepth=0;//右子树深度
//左子树一直向左
while(left)
{
leftDepth++;
left=left->left;
}
//右子树一直向右
while(right)
{
rightDepth++;
right=right->right;
}
if(leftDepth==rightDepth) return (2<<leftDepth)-1;//满二叉树的结点计算公式
int leftCount=countNodes(root->left);
int rightCount=countNodes(root->right);
return leftCount+rightCount+1;
}
};原理思路:
可以和当作普通二叉树解题的代码对比着看,会发现,其实就是多了一个终止条件,也就是下面这几行代码:
TreeNode* left=root->left;
TreeNode* right=root->right;
int leftDepth=0;//左子树深度
int rightDepth=0;//右子树深度
//左子树一直向左
while(left)
{
leftDepth++;
left=left->left;
}
//右子树一直向右
while(right)
{
rightDepth++;
right=right->right;
}
if(leftDepth==rightDepth) return (2<<leftDepth)-1;//满二叉树的结点计算公式这样我们就不用遍历所有结点了,减少了运算时间,下面说说这个多出的终止条件是什么意思。
其实就是判断一下所遍历到的子树是否为满二叉树,这样我们就可以直接利用满二叉树的公式 2^n-1 来计算出此子树的结点个数,直接返回,例如:
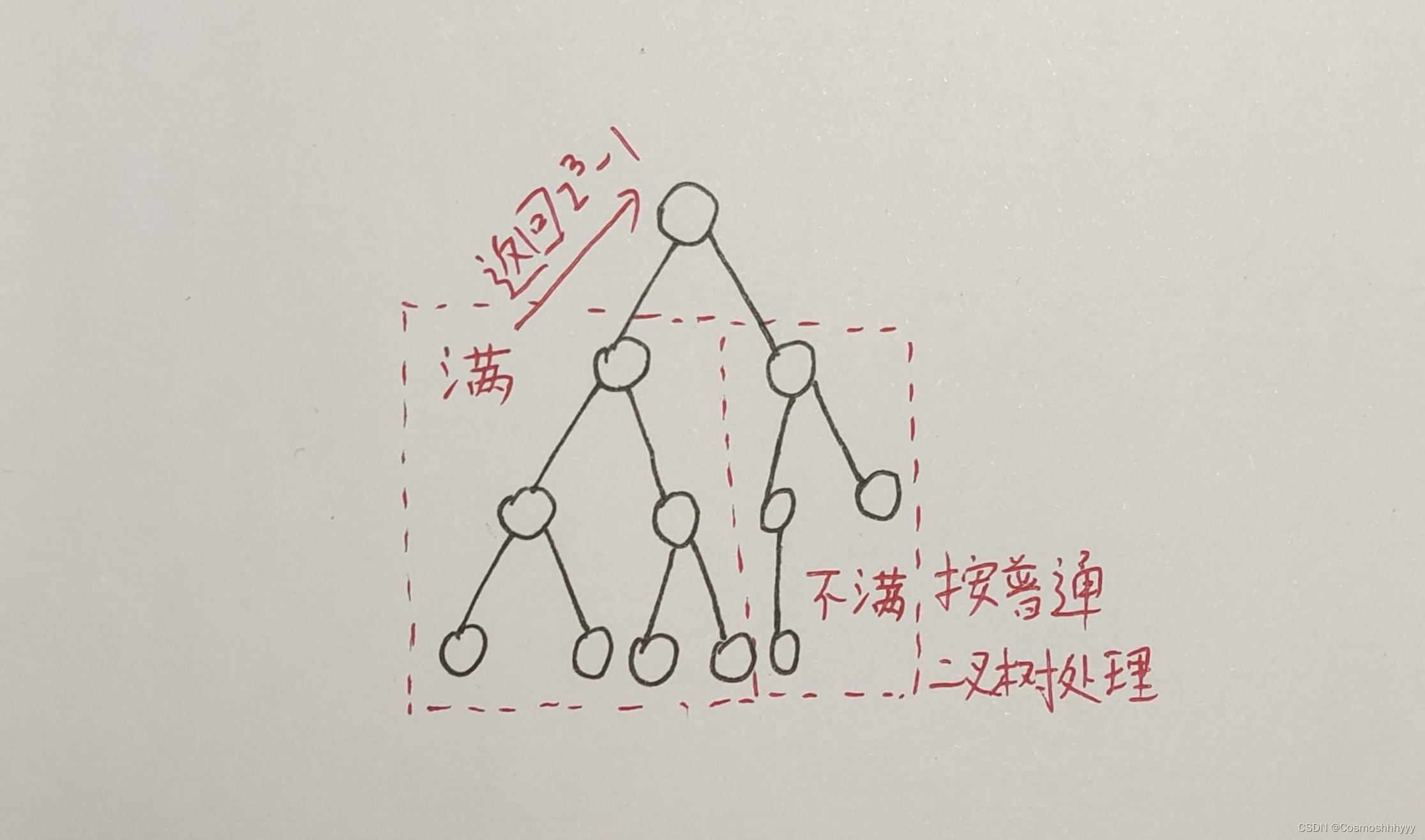
return (2<<leftDepth)-1;leftDepth也可以换成rightDepth,毕竟是相等的时候才这样返回嘛。这里用了位运算,当leftDepth=1时就等同于( 2 ^ 2 ) - 1 = 3。
然后来说说我们是如何判断该子树为满二叉树的呢,只要我们沿着子树的左侧一直向左,右侧一直向右,若两侧深度相同则就是满二叉树,也就是这几行代码:
//左子树一直向左
while(left)
{
leftDepth++;
left=left->left;
}
//右子树一直向右
while(right)
{
rightDepth++;
right=right->right;
}这时候就有人要问了,会不会出现下面这种情况:
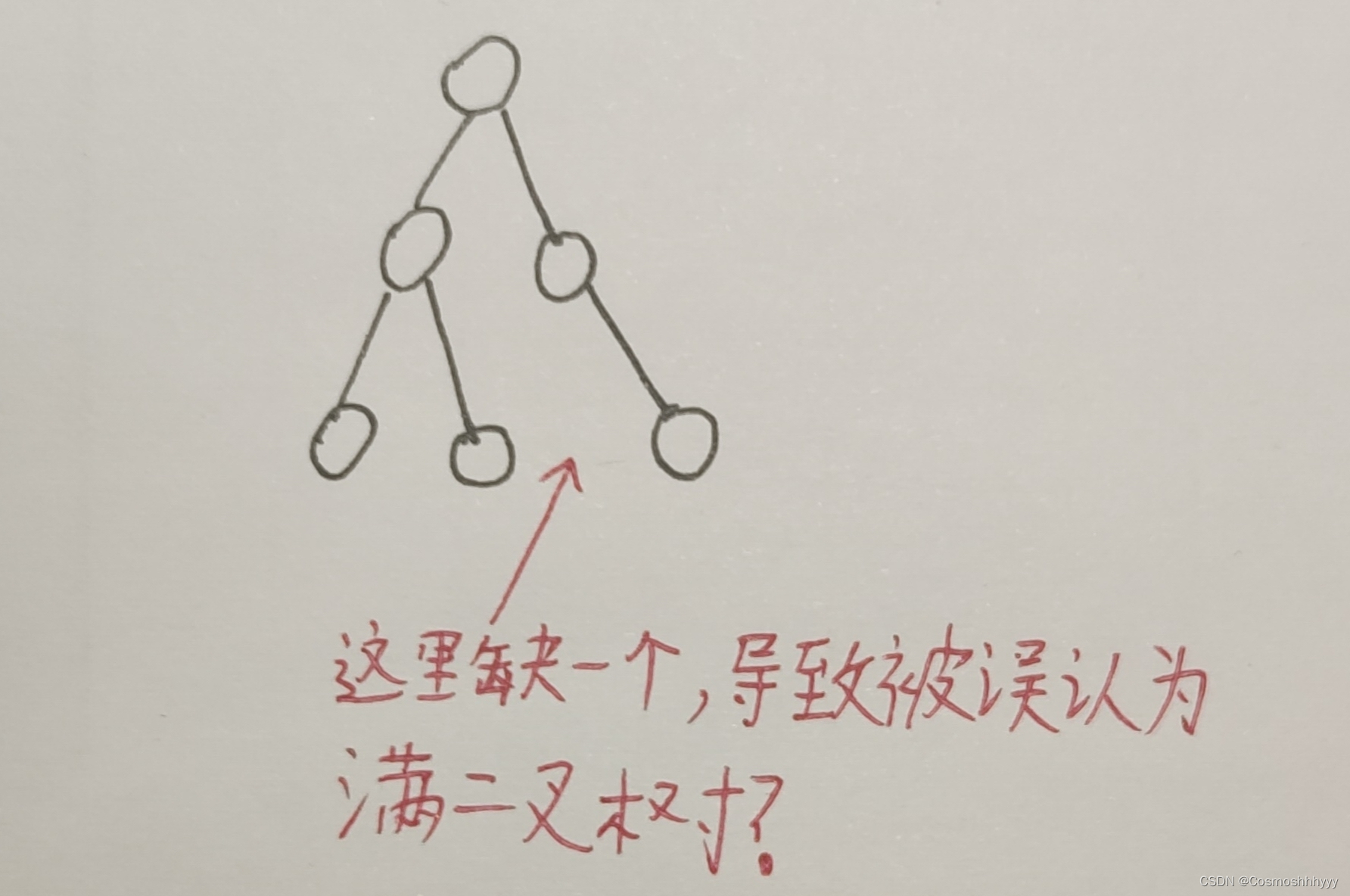
答案很明显,是不会出现这种情况的,因为题目已经说了给的是完全二叉树,这种情况都不是完全二叉树,所以显然是不会出现这种情况的,若左右深度相同,中间结点一定是满的。