6.2 图的存储与基本操作
- 概念
- 图的存储

-
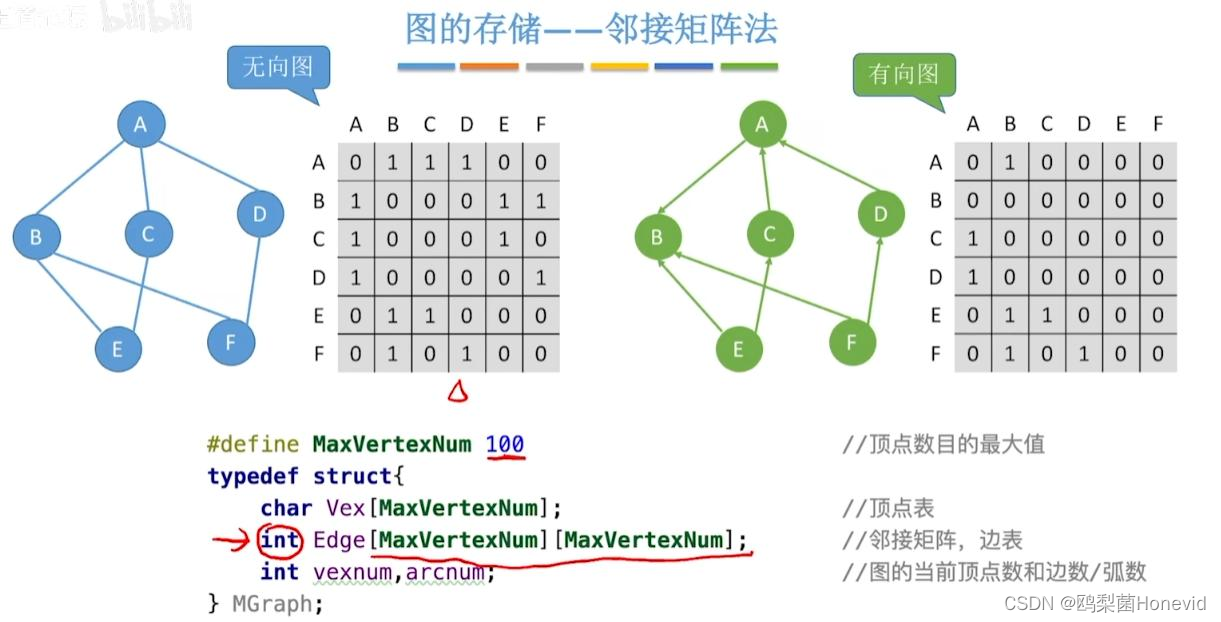
邻接矩阵存有向图和无向图
-
-
根据邻接矩阵求度:
-
无向图:第i个结点的度 = 第i行 (或第列) 的非零元素个数
-
有向图:
-
第i个结点的出度 =第i行的非零元素个数
-
第i个结点的入度 =第i列的非零元素个数
-
第i个结点的度 = 第i行、第i列的非零元素个数之和
-
-
邻接矩阵法求顶点的度/出度/入度的时间复杂度为 O(|V|)
-
-
-
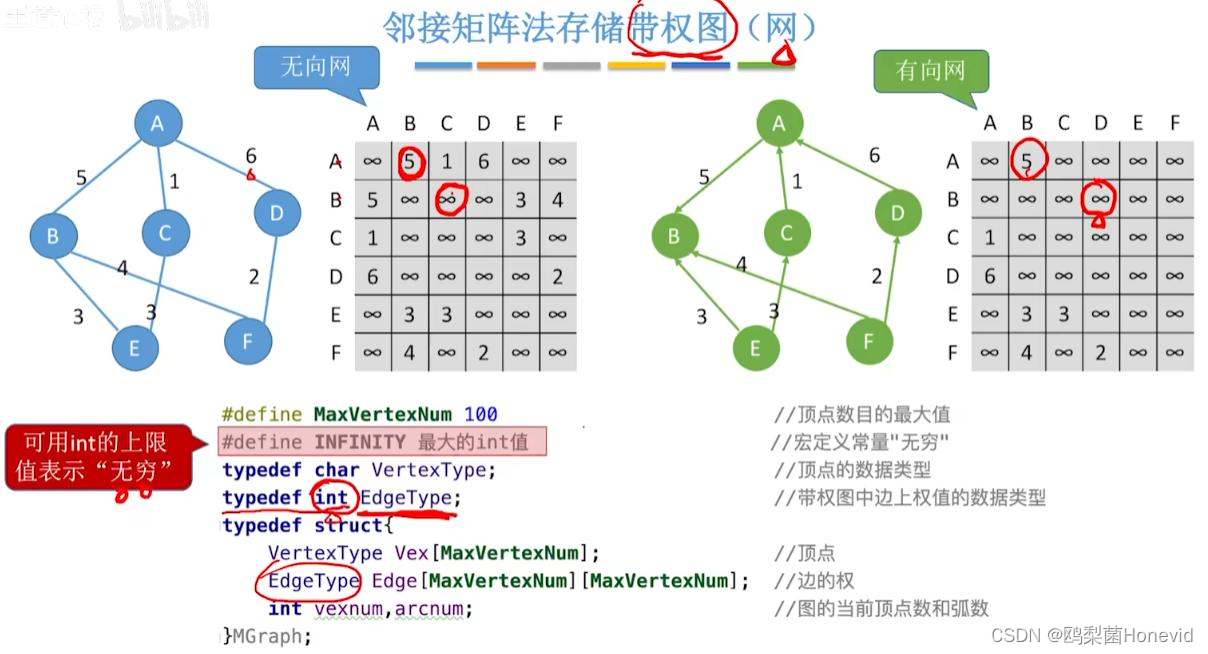
邻接矩阵存带权图(网)
-
-
0与∞都表示两点间不存在边
-
-
邻接矩阵的性能分析
-
空间复杂度:O(|V|2):只和顶点数相关,和实际的边数无关
-
适合用于存储稠密图
-
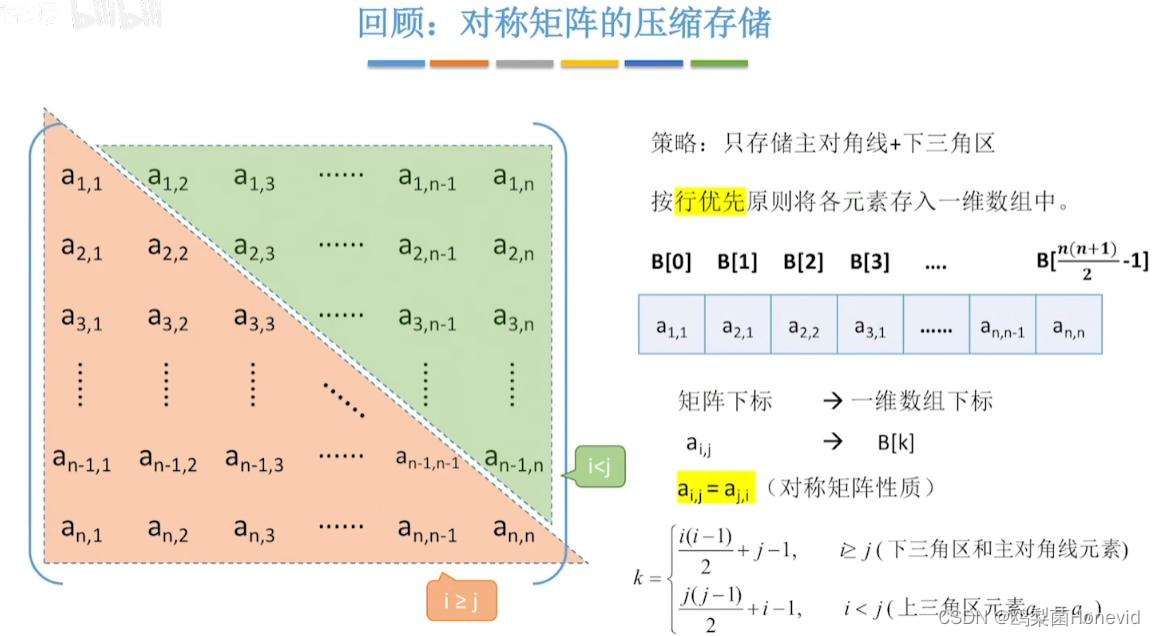
无向图的邻接矩阵是对称矩阵,可以压缩存储 (只存储上三角区/下三角区)
-
-
-
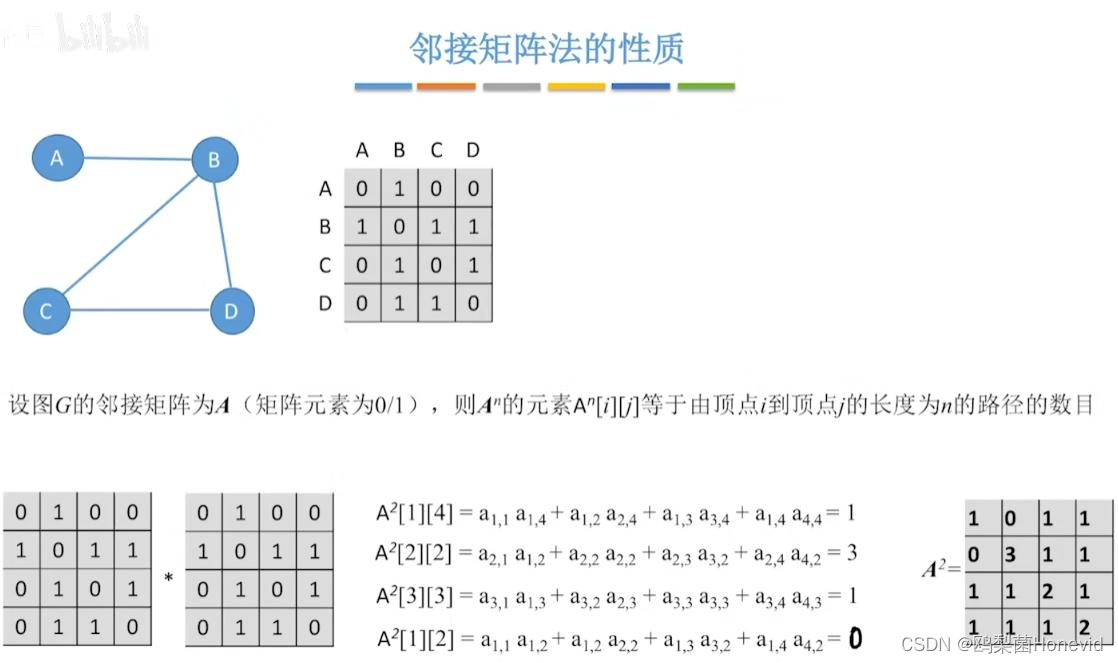
邻接矩阵的性质
-
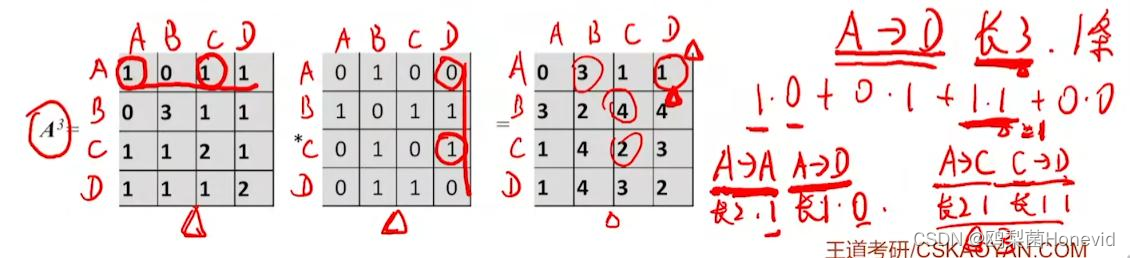
从顶点i到顶点j长度为n的路径个数求法
-
-
-

-
-
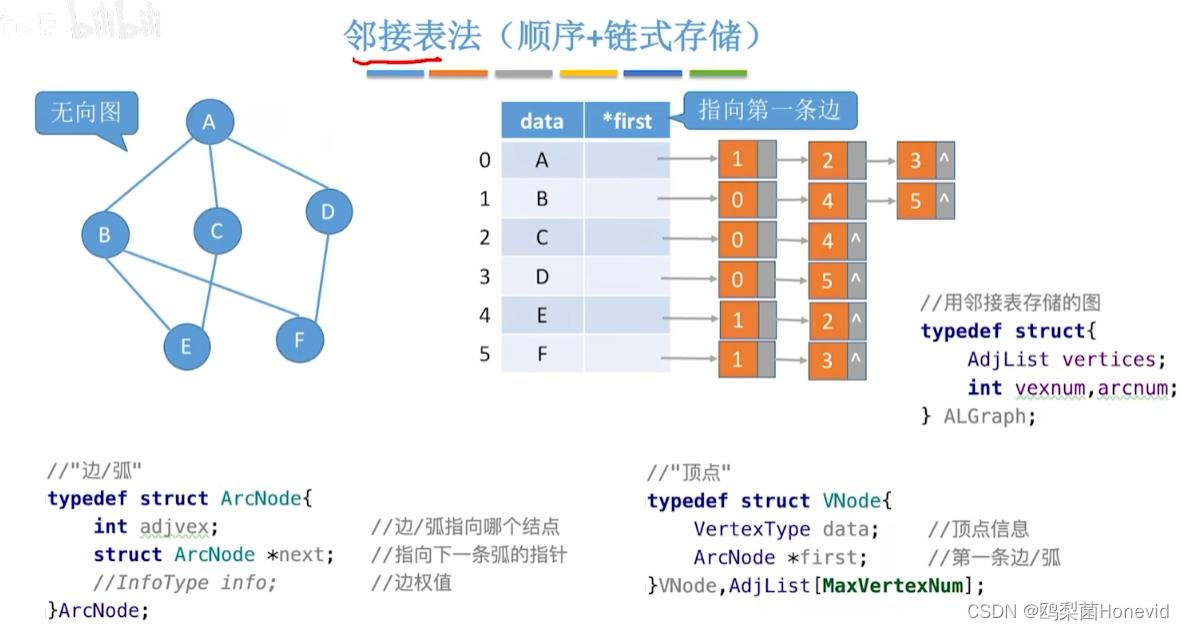
邻接表法(顺序+链式存储)
-
-
-
-
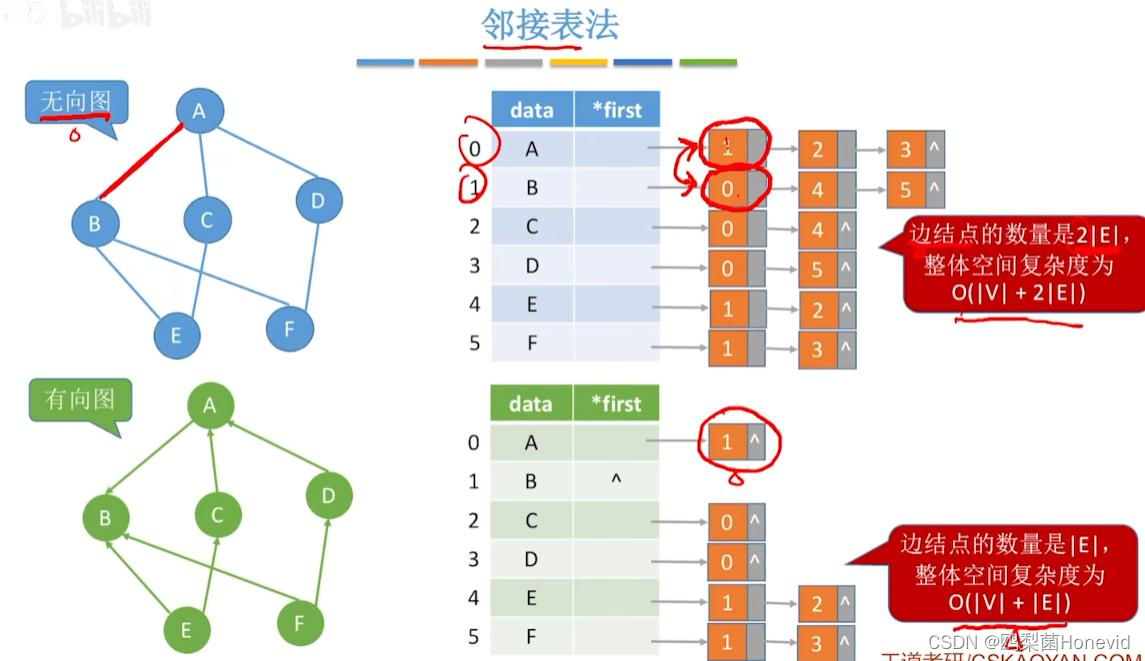
邻接表法求顶点的度、入度、出度
-
无向图:遍历顶点的边链表即可得到与该点相连的所有边,计数即为度
-
有向图:
-
出度:遍历该顶点的边链表即可得到出度,和从该点指出去的所有弧
-
入度:遍历所有顶点的边链表
-
-
-
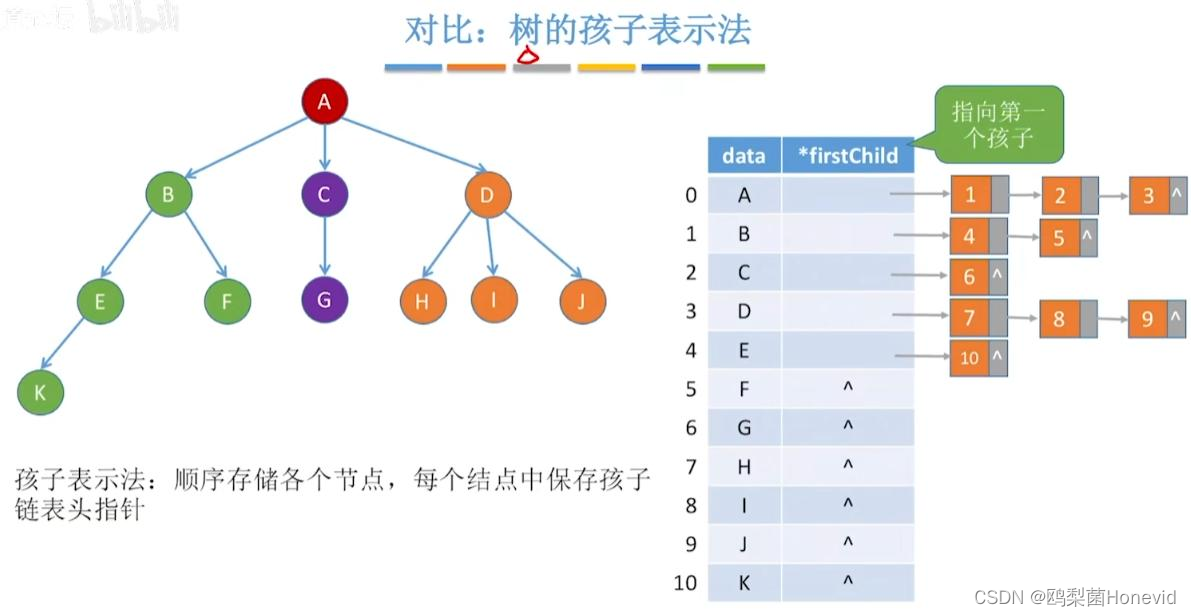
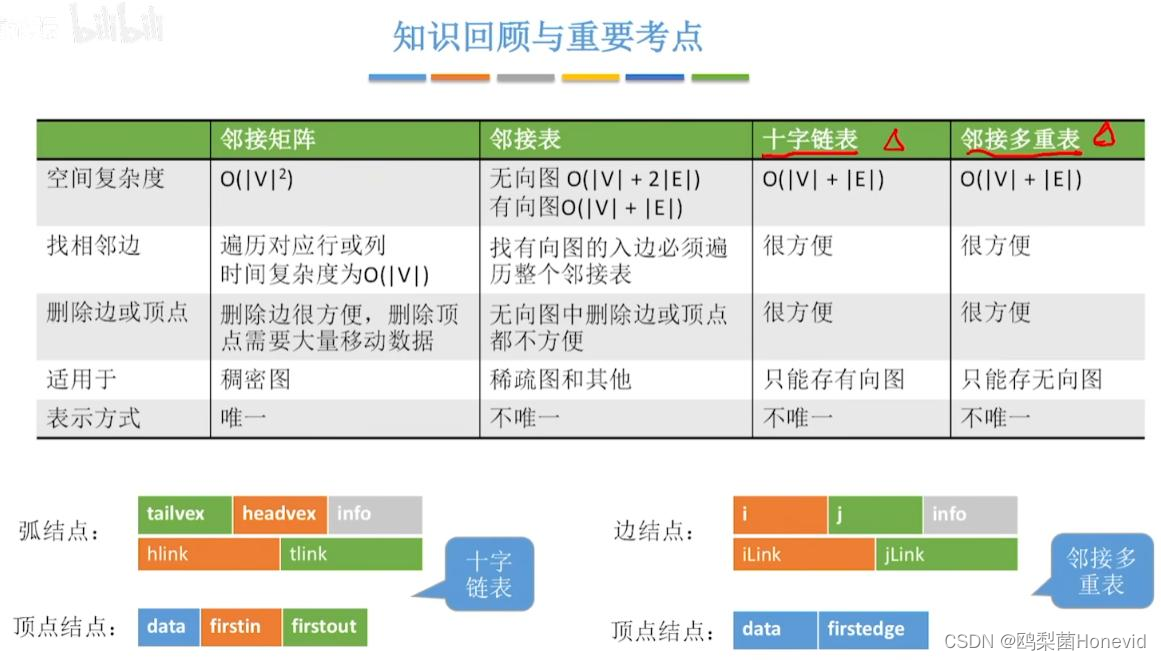
邻接表与邻接矩阵的区别 …

-
-
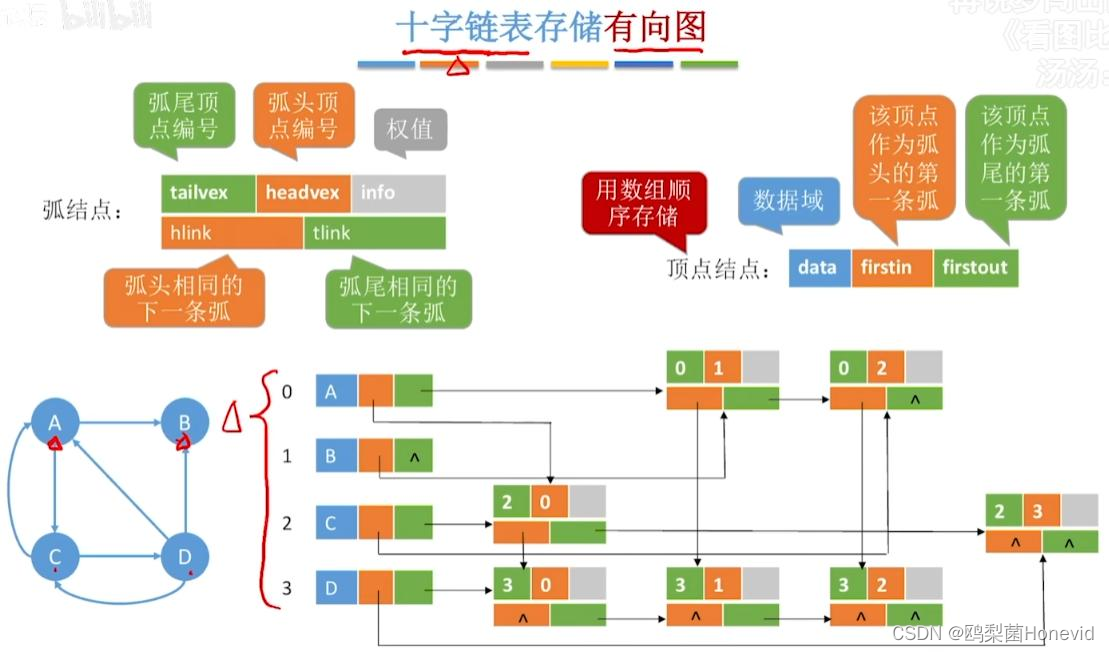
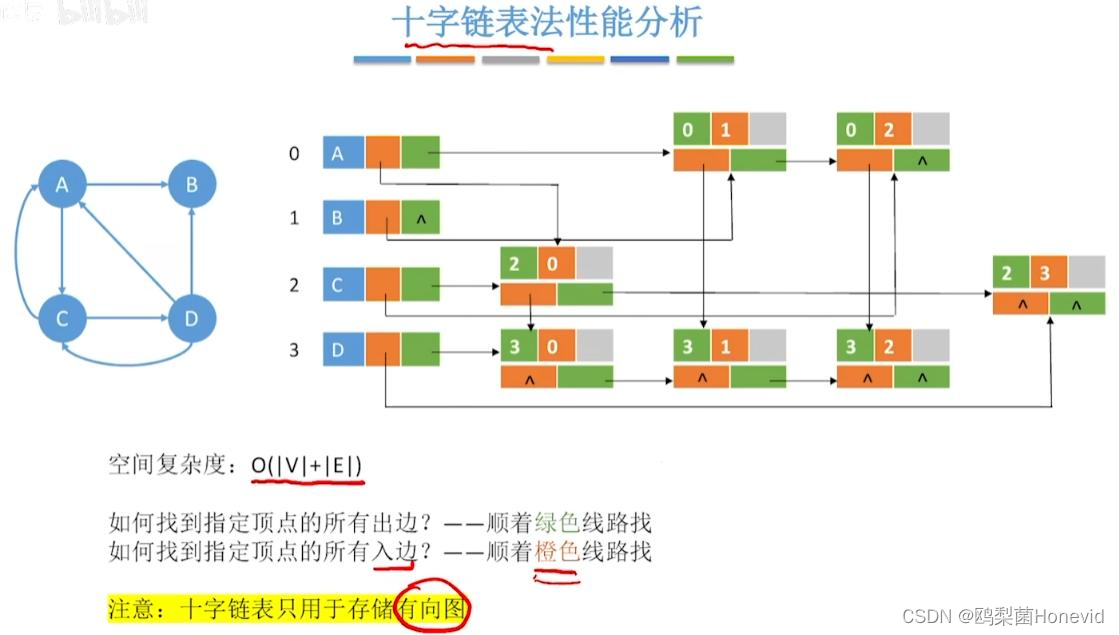
十字链表法存储有向图
-
-
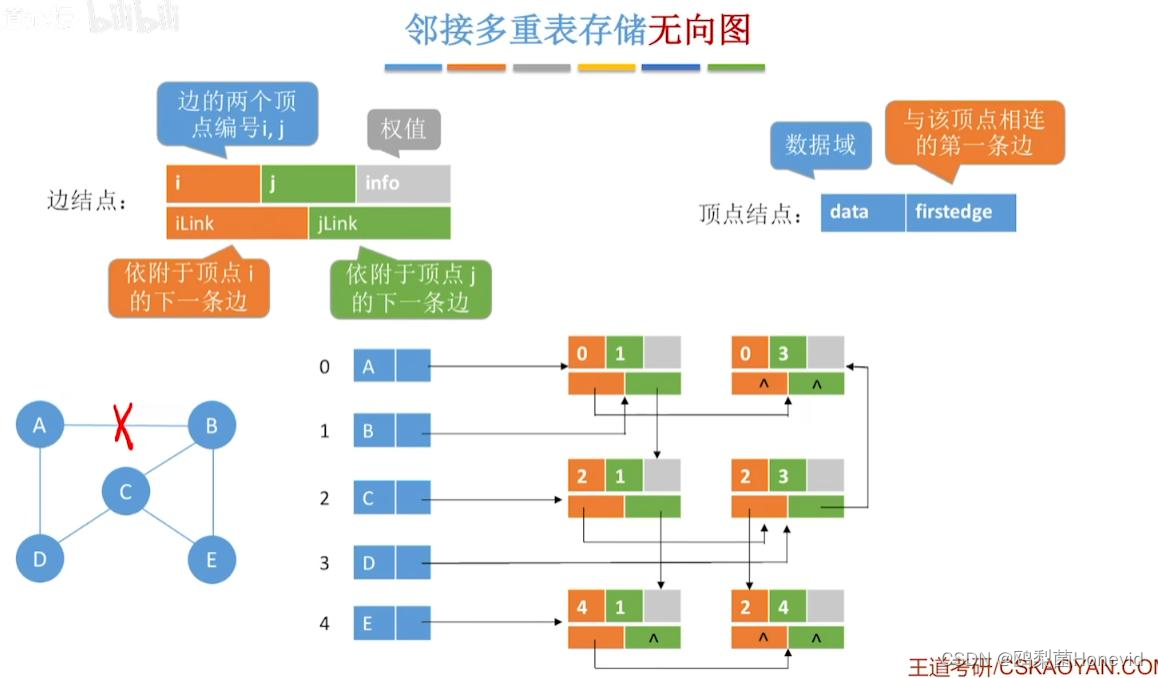
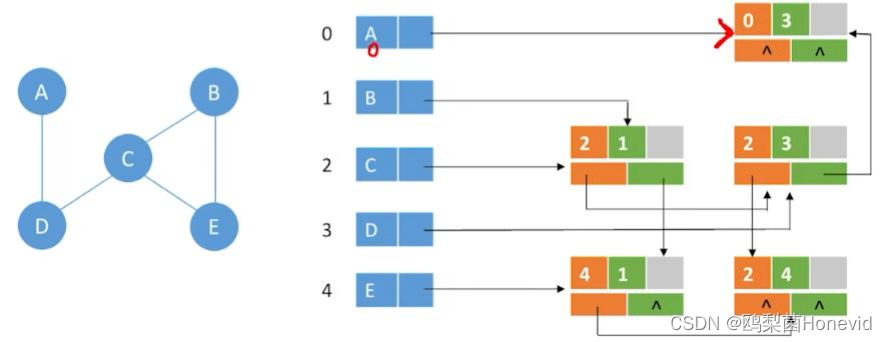
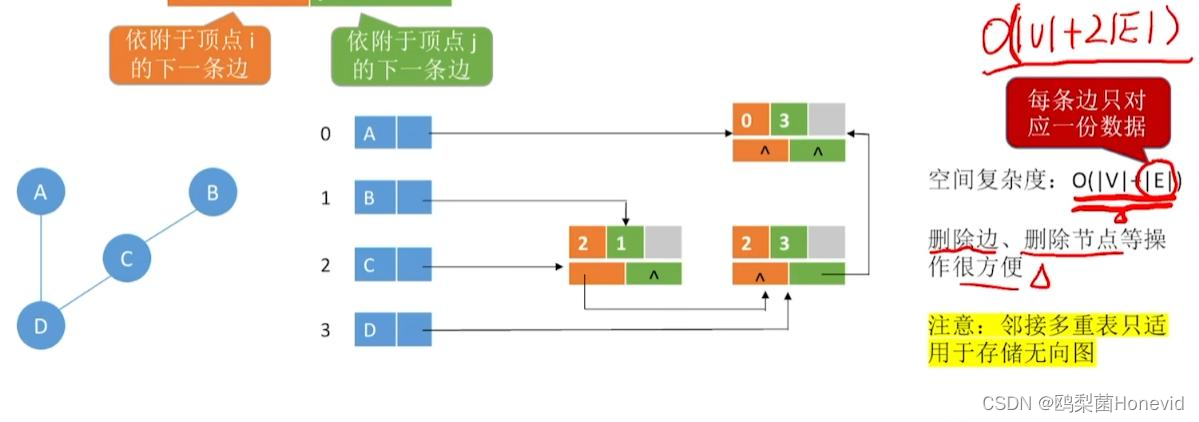
邻接多重表存储无向图
-
-
边的删除
-
点的删除
-
-
-
图的基本操作
- 理解
-
假设n个顶点,e个边的有向图用邻接表表示,则删除某个顶点v相关的所有边的复杂度为O(n+e)
-
在有向图的邻接表存储结构中,顶点v在边表中出现的次数为:顶点v的入度
- 技巧
-
若图的邻接矩阵中,除主对角线全0外,矩阵其他元素全为1,则该图一定是完全图
-
A ( n ) ( i j ) A^(n)_(ij) A(n)(ij)表示顶点i到顶点j,长度为n的路径一共有 A ( n ) ( i j ) A^(n)_(ij) A(n)(ij)条






![[word] word如何打印背景和图片? #微信#其他#经验分享](https://img-blog.csdnimg.cn/img_convert/8e46bdb2025f7b692459ac16f8ff36d8.jpeg)