注：书中对代码的讲解并不详细，本文对很多细节做了详细注释。另外，书上的源代码是在Jupyter Notebook上运行的，较为分散，本文将代码集中起来，并加以完善，全部用vscode在python 3.9.18下测试通过，同时对于书上部分章节也做了整合。

Chapter8 Recurrent Neural Networks

8.4 Recurrent Neural Networks

对$n$元语法模型，单词$x_t$在时间步$t$的条件概率仅取决于前面$n-1$个单词。对于时间步$t-(n-1)$之前的单词，如果我们想将其可能产生的影响合并到$x_t$上，需要增加$n$，然而模型参数的数量也会随之呈指数增长，因为词表$\mathcal{V}$需要存储$|\mathcal{V}{|}^n$个数字（每个可能的序列对应一个概率值），因此不如使用隐变量模型：

$$P(x_t\mid x_{t-1},\dots ,x_1)\approx P(x_t\mid h_{t-1}),$$

其中$h_{t-1}$是隐状态（hidden state），也称为隐藏变量（hidden variable），它存储了到时间步$t-1$的序列信息。通常，我们可以基于当前输入$x_t$和先前隐状态$h_{t-1}$来计算时间步$t$处的任何时间的隐状态：

$$h_t=f(x_t,h_{t-1}).$$

对于上式中的函数$f$，隐变量模型可以不是近似值，因为$h_t$可以存储到目前为止观察到的所有数据，然而这样的操作可能会使计算和存储的代价都变得昂贵。值得注意的是，隐藏层和隐状态是两个不同的概念，隐藏层是在从输入到输出的路径上（以观测角度来理解）的隐藏的层，而隐状态则是在给定步骤所做的任何事情（以技术角度来定义）的输入，并且这些状态只能通过先前时间步的数据来计算。

8.4.1 Neural Networks without Hidden States

对只有单隐藏层的多层感知机，设隐藏层的激活函数为$\varphi$，给定一个小批量样本$\mathbf{X}\in {\mathbb{R}}^{n\times d}$，其中批量大小为$n$，输入维度为$d$，则隐藏层的输出$\mathbf{H}\in {\mathbb{R}}^{n\times h}$通过下式计算：

$$\mathbf{H}=\varphi (\mathbf{X}{\mathbf{W}}_{xh}+{\mathbf{b}}_h).$$

输出层由下式给出：

$$\mathbf{O}=\mathbf{H}{\mathbf{W}}_{hq}+{\mathbf{b}}_q,$$

8.4.2 RNN with Hidden States

假设我们在时间步$t$有小批量输入${\mathbf{X}}_t\in {\mathbb{R}}^{n\times d}$，换言之，对于$n$个序列样本的小批量，${\mathbf{X}}_t$的每一行对应于来自该序列的时间步$t$处的一个样本。用${\mathbf{H}}_t\in {\mathbb{R}}^{n\times h}$表示时间步$t$的隐藏变量，计算公式如下：

$${\mathbf{H}}_t=\varphi ({\mathbf{X}}_t{\mathbf{W}}_{xh}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{hh}+{\mathbf{b}}_h).\text{\hspace{1em}(1)}$$

由于在当前时间步中，隐状态使用的定义与前一个时间步中使用的定义相同，因此称式(1)的计算是循环的（recurrent），基于循环计算的隐状态神经网络称为循环神经网络（recurrent neural network），在循环神经网络中执行循环计算的层称为循环层（recurrent layer）。对于时间步$t$，输出层的输出类似于多层感知机中的计算：

$${\mathbf{O}}_t={\mathbf{H}}_t{\mathbf{W}}_{hq}+{\mathbf{b}}_q.$$
循环神经网络的参数包括隐藏层的权重${\mathbf{W}}_{xh}\in {\mathbb{R}}^{d\times h},{\mathbf{W}}_{hh}\in {\mathbb{R}}^{h\times h}$和偏置${\mathbf{b}}_h\in {\mathbb{R}}^{1\times h}$，以及输出层的权重${\mathbf{W}}_{hq}\in {\mathbb{R}}^{h\times q}$和偏置${\mathbf{b}}_q\in {\mathbb{R}}^{1\times q}$。值得一提的是，即使在不同的时间步，循环神经网络也总是使用这些模型参数，因此循环神经网络的参数开销不会随着时间步的增加而增加。

下图展示了循环神经网络在三个相邻时间步的计算逻辑。

import torch
from d2l import torch as d2l

#循环计算（部分）的两种计算方法
X, W_xh = torch.normal(0, 1, (3, 1)), torch.normal(0, 1, (1, 4))
H, W_hh = torch.normal(0, 1, (3, 4)), torch.normal(0, 1, (4, 4))
torch.matmul(X, W_xh) + torch.matmul(H, W_hh)
torch.matmul(torch.cat((X, H), 1), torch.cat((W_xh, W_hh), 0))

8.4.3 Character-Level Language Models Based on RNN

接下来介绍如何使用循环神经网络来构建语言模型。设小批量大小为1，批量中的文本序列为"machine"。为了简化后续部分的训练，考虑使用字符级语言模型（character-level language model），将文本词元化为字符而不是单词。下图演示了如何通过基于字符级语言建模的循环神经网络，使用当前的和先前的字符预测下一个字符。

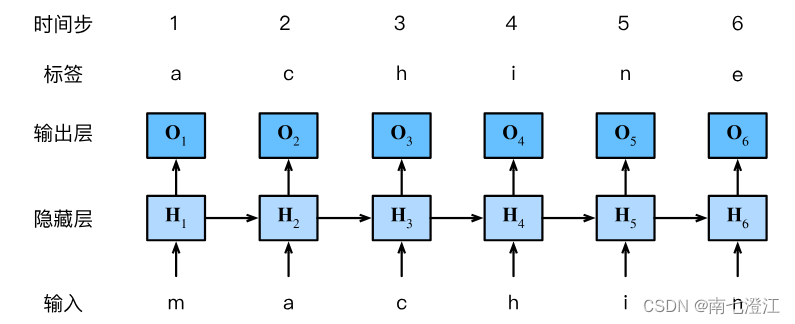
在实践中，我们使用的批量大小为$n>1$，每个词元都由一个$d$维向量表示。因此，在时间步$t$输入${\mathbf{X}}_t$将是一个$n\times d$矩阵。

8.4.4 Perplexity

我们可以通过计算序列的似然概率来度量模型的质量，然而这难以理解、难以比较，因为较短的序列比较长的序列更有可能出现。为了解决这个问题，我们可以运用信息论。如果想要压缩文本，我们可以根据当前词元集预测的下一个词元。一个更好的语言模型应该能让我们更准确地预测下一个词元，即它应该允许我们在压缩序列时花费更少的比特，所以我们可以通过一个序列中所有的$n$个词元的交叉熵损失的平均值来衡量模型的质量：

$$\frac{1}{n}\sum _{t=1}^n-\log P(x_t\mid x_{t-1},\dots ,x_1)$$

其中$P$由语言模型给出，$x_t$是在时间步$t$从该序列中观察到的实际词元。这使得不同长度的文档的性能具有了可比性。困惑度（perplexity）是上式的指数：

$$\exp \left(-\frac{1}{n}\sum _{t=1}^n\log P(x_t\mid x_{t-1},\dots ,x_1)\right).$$

困惑度的最好的理解是“下一个词元的实际选择数的调和平均数”。

• 在最好的情况下，模型总是完美地估计标签词元的概率为1。在这种情况下，模型的困惑度为1。
• 在最坏的情况下，模型总是预测标签词元的概率为0。在这种情况下，困惑度是正无穷大。
• 在基线上，该模型的预测是词表的所有可用词元上的均匀分布。在这种情况下，困惑度等于词表中唯一词元的数量。事实上，如果我们在没有任何压缩的情况下存储序列，这将是我们能做的最好的编码方式。因此，这种方式提供了一个重要的上限，而任何实际模型都必须超越这个上限。